
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорія незбуреного руху супутника.Содержание книги Поиск на нашем сайте
Поняття про гравітаційне поле Землі. ШСЗ є небесними тілами, що рухаються на значній відстані від земної поверхні. Відомо що всякі тіла, які розміщені в космічному просторі взаємодіють між собою утворюючи силу взаємодії, яка називається силою тяжіння (притягання)
Формула (1.3) показує, що величина тіла тяжіння прямо пропорційна добутку мас тіл, що взаємодіють і обернено пропорційна квадрату відстані між тілами. Очевидно, що ця сила уде виникати при взаємодії Землі і супутника. Іншою силою, що виникає при взаємодії тіл є відцентрова сила пов’язана з обертанням тіл в просторі. Величина цієї сили:
Залежить від кутової сили і відстані. Сумою цих двох сил є сила ваги, яка характеризує те прискорення, яке набуває одинична маса за одиницю часу. Сила ваги в різних точках простору має різне значення, оскільки залежить як від взаємного розміщення тіл, так і від відстані між ними. Сукупність сил ваги в космічному просторі і на поверхні Землі утворює гравітаційне поле Землі. Гравітаційне поле є змінним і векторним. Найбільш об’єктивною характеристикою гравітаційного поля є його потенціал. Потенціал визначається формулою:
в формулі (1.5) нехтується масою супутника, яка є нескінченно малою в порівнянні з масою Землі.
Величина (1.6) називається гравітаційним параметром гравітаційного поля Землі, тоді:
Закони руху ШСЗ. Рух супутників по орбіті навколо Землі описується законами Кеплера, які для випадку дослідження руху супутників формулюються так. 1-й закон: орбітою супутника може бути плоска крива другого порядку (коло, еліпс, парабола, гіпербола) в одному із фокусів якої знаходиться Земля. Розглянемо коли орбітою є еліпс. Найближчою точкою орбіти супутника до Землі є точка Перігей, а найбільш віддалена Апогей. Всяка орбіта характеризується двома параметрами: а – велика піввісь, е – ексцентриситети.
Положення супутника на орбіті визначають двома параметрами: r відстань або радіус-вектор супутника і Істина аномалія – кут утворений радіус-вектором супутника і напрямком на Перигей. Цей кут завжди відраховується від напрямку на перігей проти ходу годинникової стрілки і може приймати значення від 0 до 360. 2-й закон: радіус-вектор супутника в рівні проміжки часу описує рівновеликі площі секторів. Нехай супутник один раз находиться в точці С1, а другий в точці С2. Відомо:
У відповідності до другого закону
З аналізу (1.10) встановлюємо, що супутник по орбіті рухається нерівномірно, в районі Перигею ця швидкість досягає максимального значення, а в районі Апогею швидкість руху супутника мінімальна. 3-й закон: відношення квадратів періодів обертання двох супутників по орбітах є величиною постійною і дорівнює відношенню кубів великих півосей їх орбіт.
Якщо супутники, що рухаються мають різну масу то
З-й закон Кеплера дозволяє по відомих періодах обертань супутників визначити параметри орбіти і навпаки. Рух супутників по орбіті, який проходив би у відповідності до законів Кеплера називається незбуреним рухом. Рух супутників в реальному гравітаційному полі Землі завжди пов’язаний із збуренням тих чи інших параметрів руху цим гравітаційним полем і тому називається збуреним рухом. Елементи орбіт ШСЗ. Елементами орбіт називають величини, які характеризують як саму орбіту так і її розміщення в просторі, а також положення супутника на орбіті. Відомо, що орбітою супутника може бути плоска крива коло, еліпс, парабола, гіпербола. Для характеристики орбіти як геометричної фігури достатньо знати: а – велика піввісь, е – ексцентриситети.
Для характеристики орбіти супутника в просторі використовують два параметри: довгота висхідного вузла орбіти, нахил орбіти до екватора. Орбіта всякого супутника буде перетинати площину небесного екватора в двох точках, які називають висхідною точною орбіти і низхідною точкою орбіти. Назви пов’язані із рухом супутника довкруги Землі. Нехай тачка Кутом нахилу орбіти називають кут утворений площиною орбіти з площиною небесного екватора, цей кут від 0 до 90. Наступні дві координати визначають положення супутника на орбіті. Цими координатами є висота Перігею і істина аномалія. Висотою перігея
Положення супутника розглядається кутом істинної аномалії
Наступні елементи орбіти: середній рух супутника середня аномалія ексцентрична аномалія Нехай ми маємо орбіту супутника у вигляді еліпса. Відомо на основі ll закону Кєплера, що рух супутника по орбіті відбувається з різною швидкістю в районі перигея- максимальна, апогея – мінімальна. Для характеристики руху супутника по орбіті часто використовують так званий середній рух який дорівнює середньому значенню швидкості руху супутника по орбіті. Опишемо коло радіуса а і спроектуємо на це коло супутник, кут утворений напрямком на точку перигея орбіти і на точку C`, яка є проекцією супутника на орбіту в виді кола радіуса а, називається ексцентричною аномалією супутника (Е). Нехай супутник сферичну відстань
|
||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 434; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.210.196 (0.009 с.) |

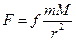 , (1.3)
, (1.3) – гравітаційна стала,
– гравітаційна стала, 
 , (1.4)
, (1.4) , (1.5)
, (1.5) , (1.6)
, (1.6) , (1.7)
, (1.7)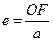 , (1.8)
, (1.8) – орбіта коло;
– орбіта коло; – парабола;
– парабола; – еліпс;
– еліпс; – гіпербола.
– гіпербола. – істина аномалія.
– істина аномалія.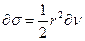

 повинна бути стала, звідси
повинна бути стала, звідси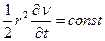 , (1.10)
, (1.10)
 також не повинно бути сталим.
також не повинно бути сталим.  , (1.11)
, (1.11) , (1.12)
, (1.12) є точка весняного рівнодення. Кут утворений в площині небесного горизонту напрямками на точку весняного рівнодення і на точку висхідного вузла називають довготою висхідного вузла орбіти. Довгота висхідного вузла завжди відраховується від напрямку на точку весняного рівнодення, проти ходу годинникової стрілки і до напрямку на висхідний вузол. Може приймати значення від 0 до 360.
є точка весняного рівнодення. Кут утворений в площині небесного горизонту напрямками на точку весняного рівнодення і на точку висхідного вузла називають довготою висхідного вузла орбіти. Довгота висхідного вузла завжди відраховується від напрямку на точку весняного рівнодення, проти ходу годинникової стрілки і до напрямку на висхідний вузол. Може приймати значення від 0 до 360. називається сферична відстань точки перігея від висхідного вузла орбіти відрахована по самій орбіті.
називається сферична відстань точки перігея від висхідного вузла орбіти відрахована по самій орбіті.
 , (1.13)
, (1.13) по орбіті пройшов за час t. Швидкість руху на цій ділянці буде максимальною Vmax. Середня швидкість на цій ділянці Vo<Vmax. Тому по орбіті в вигляді кола супутник за час t, рухаючись зі швидкістю Vo пройде дугу ПС". Кут утворений напрямком на точку перигея і напрямком на точку С`` називається середньою аномалією M.
по орбіті пройшов за час t. Швидкість руху на цій ділянці буде максимальною Vmax. Середня швидкість на цій ділянці Vo<Vmax. Тому по орбіті в вигляді кола супутник за час t, рухаючись зі швидкістю Vo пройде дугу ПС". Кут утворений напрямком на точку перигея і напрямком на точку С`` називається середньою аномалією M.


