
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Визначення густини твердих тіл правильної геометричної формиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ЗМІСТ
Вступ............................................................................................................ 4
1. Лабораторна робота №1............................................................ 5 Визначення густини твердих тіл правильної геометричної форми
2. Лабораторна робота №2........................................................... 16 Визначення прискорення сили земного тяжіння за допомогою математичного маятника та декремента загасання коливань маятника
3. Лабораторна робота №3........................................................... 23 Вивчення пружних властивостей кісткової тканини
4. Лабораторна робота №4............................................................ 31 Вимірювання коефіцієнта поверхневого натягу
5. Лабораторна робота №5............................................................ 40 Визначення коефіцієнту в´язкості рідини методом Стокса
6. Лабораторна робота №6............................................................ 49 Зняття спектральної характеристики вуха на порозі чутності
ДОДАТКИ………………………………………………………………….......... 56 1. Обчислення похибок для прямих вимірювань....................................................56 2. Обчислення похибок для непрямих вимірювань................................................56 3. Коефіцієнти Стьюдента............................................................................................57 4. Схема оформлення протоколу................................................................................58
Вступ Медична та біологічна фізика є однією з фундаментальних дисциплін, викладання якої в університеті відповідає цілям змісту медичної освіти, що закладає фундамент наукового мислення, формує пізнавальний стиль майбутнього фахівця і є обов'язковим для вивчення. Лабораторні заняття спрямовані на оволодіння студентами практичних навичок в галузі медичної та біологічної фізики, зокрема використання діагностичного та фізіотерапевтичного електронного обладнання, оптичних методів у медицині тощо. Заняття орієнтовані на вирішення пошуку шляхів підвищення якості підготовки лікарів, які вміють провести науково-обґрунтований медико-біологічний експеримент, здатних до фундаментальної наукової роботи, готових до здобуття навичок роботи з технікою в медицині. В результаті опанування курсом студенти повинні ЗНАТИ: - пояснювати фізичні основи та біотичні механізми дії зовнішніх факторів на біологічні об’єкти, зокрема на органи та системи людини; - пояснювати фізичні основи діагностичних і фізіотерапевтичних (лікувальних) методів, що застосовуються в медичній апаратурі; - трактувати загальні фізичні та біофізичні закономірності, що лежать в основі життєдіяльності людини; - техніку безпеки при роботі з апаратурою. УМІТИ: - виконувати основні фізичні вимірювання; - обробляти результати вимірювань та використовувати для цього обчислювальні засоби.
ЛАБОРАТОРНА РОБОТА №1
Визначення густини твердих тіл Правильної геометричної форми
Мета роботи: навчитися вимірювати довжину та масу твердих тіл з метою визначення густини речовини та набути навики обробки результатів непрямих вимірювань. Необхідні прилади і матеріали: технічні та торсійні ваги, штангенциркуль, мікрометр, зразки тіл різних геометричних форм.
Опис приладів, що використовуються в роботі Прилади для вимірювання маси
Вимірювання маси виконується шляхом точного зважування на аналітичних або торсійних (обертальних) вагах.
Конструкція та принцип зважування на торсійних вагах Зовнішній вигляд торсійних ваг представлено на рис.9. Вони відрізняються від аналітичних ваг як за конструкцією, так і за принципом дії. Зважування на них проводиться також дуже швидко і з досить великою точністю. Межа вимірювань приводиться на передній панелі ваг. Торсійні ваги бувають двох типів: Ø з нерухомою шкалою циферблата й рухомою стрілкою або Ø з рухомою шкалою циферблата й нерухомою стрілкою. Механізм ваг (рис.9) змонтований на металічній плиті 1 і прикритий корпусом 2. Плита опирається на прикріпленій до неї підпорі та на двох регульованих гвинтах 3, що служать для установки ваг за рівнем. Правильна установка ваг контролюється рівнем 4, що знаходиться в передній частині корпуса ваг. Чаша 5 знаходиться на кінці рухомого важелю й захищена скляними дверцятами 6, які оберігають зважуване тіло від впливу зовнішнього середовища. Праворуч від корпусу знаходиться регулювальна головка 7, що використовується для виведення нерухомої стрілки на нульову поділку шкали. Головка 7 обертає барабан зі шкалою, за якою визначають вимірювану величину. Праворуч корпусу знизу знаходиться головка 9, що дозволяє блокувати рухливий важіль у випадку довготривалого простою ваг чи транспортування.
Приготування до зважування
1. При закритих дверцятах слід розблокувати ваги шляхом повороту головки 9 на 1800С у положення „0” (в положенні „z” ваги заблоковано). 2. Після цього повертають лівою головкою 8 шкалу доти, поки рухома стрілка не займе положення на червоній рисці, що визначає положення рівноваги важеля. 3. Далі правою головкою 7 наводять нерухому стрілку на нульову поділку шали.
Порядок зважування
1. Відкрити дверцята 6 ваг. 2. Предмет, призначений до зважування, акуратно щипцями покласти на чашу 5 чи підвісити на крючок. 3. Закрити дверцята 6. 4. Ліву головку 8 повернути лівою рукою від себе доти, поки рухома стрілка не виявиться на червоній рисці. Поворот головки зумовлює поворот рухомої шкали. 5. Масу зважуваного предмету визначають за рухливою шкалою в точці, на яку вказує стрілка. 6. Після закінчення вимірювання встановити шкалу за допомогою головки 8 у вихідне (нульове) положення, акуратно зняти зважуваний предмет і закрити дверцята.
Порядок виконання роботи 1. Ознайомитися з будовою вимірювальних приладів. 2. Перед початком вимірювань перевірити правильність установки і рівновагу ваг, нульові відліки штангенциркуля і мікрометра. Встановити похибки приладів. 3. Виконавши кілька попередніх вимірювань, навчитися працювати з приладами. 4. Визначити масу зразків. Зважування кожного зразка здійснюється один раз. Абсолютна похибка при зважуванні маси рівна половині точності ваг. 5. Виміряти лінійні розміри зразків з допомогою штангенциркуля та мікрометра. Вимірювання кожної величини необхідно провести не менше семи разів у різних місцях зразка. 6. Обчислити середнє значення вимірюваних величин і їх середні абсолютні похибки (див додатки 1 і 2, що приведено в кінці посібника). 7. Результати вимірювань для вказаного викладачем зразка занести у відповідні таблиці (див. таблиці 1-2). 8. Обчислити величину густини зразків і оцінити абсолютну та відносну похибки (див. приклад розрахунку похибки, який приведено нижче), результати занести в таблицю 3.
І. Найменування тіла – циліндр.
Таблиця №1. Вимірювання діаметра циліндра
Таблиця №2. Вимірювання висоти циліндра
Таблиця №3. Визначення густини тіла циліндричної форми
Приклад розрахунку похибки
1. Обчислити середнє значення густини тіла за формулою:
2. Знайти абсолютну похибку вимірювань за формулою:
де Оскільки
то формула для розрахунку абсолютної похибки визначення густини тіла циліндричної форми набуде такий кінцевий вигляд:
3. Обчислити відносну похибку визначення густини згідно формули:
Зміст звіту Формули для розрахунку густини, абсолютної та відносної похибок визначення густини для кожного з наданих викладачем тіл (паралелепіпед, куля чи циліндр); таблиці результатів; оцінка похибок вимірювань, кінцевий результат, висновки.
5. Контрольні питання
1. Як побудований кожний з вимірювальних приладів (штангенциркуль, мікрометр, аналітичні та торсійні ваги)? 2. Що таке штангенциркуль, ноніус і принцип вимірювання довжини тіл з їх допомогою? 3. Будова мікрометра та принцип вимірювання довжини з його допомогою. 4. Яка точність вимірювання штангенциркулем, мікрометром і технічними вагами, що використовуються в роботі? 5. Які межі вимірювання даними приладами? 6. Як визначається абсолютна похибка окремих прямих вимірювань? 7. Як оцінити похибку непрямих вимірювань? 8. Чи співпадають між собою – в межах похибок – дані вимірювання одного і того ж тіла, зроблені на різних ділянках? 9. Як можна встановити, що відхилення форми вимірюваного тіла від правильної носить випадковий, або, навпаки, регулярний характер?
Література
1.В.М. Авдусь. Практикум по загальній фізиці. М.– 1971.– С. 6-30. 2.В.Є.Винниченко. Фізичний практикум. Київ: „Радянська школа”.– 1959. 3.Эссаулова И.А. и др. Руководство к лабораторным работам по медицинской и биологической физике.М.: „Высшая школа”.– 1987.
ЛАБОРАТОРНА РОБОТА №2
Порядок виконання роботи Завдання 1. Визначення прискорення сили тяжіння. 1. За допомогою лінійки знайти довжину дротини. 2. За допомогою штангенциркуля виміряти діаметр кулі в різних напрямках. 3. Відхилити металеву кулю на невеликий кут (3-4°) і відпустити. Коливання повинні відбуватися в одній вертикальній площині. 4. Пропустивши декілька коливань, лічбою „нуль” пустити в хід секундомір у момент проходження маятником положення рівноваги. Для точного визначення положення рівноваги маятника під час коливання на стійці за маятником закріплюють на рівні ока екран із міліметровою шкалою, на якій проводять вертикальну лінію, що відповідає положенню рівноваги. При рівновазі маятника дротина і лінія на екрані повинні лежати в одній вертикальній площині. Перед початком відліку коливань око має бути проти дротини, яка повинна закривати проведену на екрані лінію. 5. Величини 6. Відлічивши 50 повних коливань, зупинити секундомір і знайти час, що відповідає 50 повним періодам коливань і визначити період Т тапохибку. Результати вимірювань занести у звітну таблицю №2. 7. Пункт 6 повторити щонайменше 5 разів. 8. Визначити прискорення вільного падіння g за формулою 9. Визначити похибку ∆g прискорення вільного тяжіння: оскільки
відносна похибка визначається за формулою: В даному випадку більш зручно буде знайти спочатку відносну похибку за формулою:
Звітна таблиця №1.
Звітна таблиця №2.
Завдання 2. Визначення декремента загасання маятника і коефіцієнта загасання. Спосіб 1 1.Виводять маятник із положення рівноваги на невеликий кут (3-4°). 2.Фіксують значення величини амплітуди 3. Записують моменти часу, через які амплітуда коливань зменшується на 2,5 мм. Для цього користуються міліметровою лінійкою, яку розміщено на стінці позаду маятника. 4. Будують залежність амплітуди коливань від часу в напівлогарифмічному масштабі. За нахилом кривої 5.Знаючи коефіцієнт загасання Спосіб 2 1.Визначають кількість коливань, за які амплітуда коливань зменшується в е разів. Для цього також використовують міліметрову шкалу, яку розміщено на стінці позаду маятника. Використовуючи формулу 2. Порівнюють отримані значення коефіцієнтів
Таблиця №3 Література 1. Ессаулова И.А. и др. Руководство к лабораторным работам по медицинской и биологической физике.:М., „Высшая школа”, 1987. 2. І.М.Кучерук, І..Т. Горбачук, П.П. Луцик. Загальний курс фізики. Механіка. Молекулярна фізика і термодинаміка.:Київ, „Техніка”,1999, т.1.С.209-242. 3. Бранков Г. Основы биомеханики.- М.: Мир, 1981. 4. Ємчик Л., Кміт Я. Медична і біологічна фізика.- Львів: Світ, 2003. 5. Медична і біологічна фізика./ За ред. О.В.Чалого. Підручник для студентів вищих медичних закладів освіти ІІІ-ІV рівнів акредитації.- К.: ВІПОЛ, 2005. 6. Ремизов А.Н. Медицинская и биологическая фізика: Учеб. для мед.вузов.- М.: Высшая школа, 1996. 7. Федишин Я.І. Фізика з основами біофізики. Львів: Світ, 2005.
ЛАБОРАТОРНА РОБОТА №3
Рис.3.
При малих кутах зсуву відносна деформація Дослідно встановлено, що відносний зсув пропорційний тангенціальній напрузі, тобто Діаграма напруг Діаграма напруг – це залежність напруги З рис.4 видно, що лінійна залежність
За межею пружності в тілі виникають залишкові деформації. Після припинення дії сили зворотний хід кривої йде по лінії СЕ. На ділянці ВD деформація зростає без збільшення напруги, тобто тіло ніби "тече". Ця ділянка кривої називається областю текучості. Матеріали, для яких область текучості значна, називаються в’язкими, а тіла, для яких вона практично відсутня, називають крихкими. В областітекучості здійснюється холодна обробка металу: кування, штампування, плющення, протяжка тощо. При подальшому навантаженні зразка (за т. D) відбувається спочатку зміцнення матеріалу до межі міцності ( В даній роботі вивчається тільки область пружних деформацій, які виникають в стержні при його вигині під дією навантаження. Стріла прогину буде тим більшою, чим більше навантаження. Крім того, вона залежить від форми стержня, його розмірів і матеріалу, з якого він виготовлений. Вимірявши експериментально стрілу прогину стержня, можна обчислити модуль Юнга. Вивід розрахункової формули для деформації вигину досить складний, тому тут його не приводимо. Робоча формула для визначення модуля Юнга має вид:
де В деяких областях медицини (особливо в хірургії, стоматології й ортопедії) при вивченні опорно-рухового апарату людини в питаннях протезування важливими є знання пружних властивостей тканин організму і, зокрема, кісткової тканини. Будова кісткової тканини досить складна. В її склад входять органічний матеріал (головним чином колаген) і неорганічні з'єднання, що містять кальцій, фосфор і ін. Колаген в кістці утворює фібрили – тонкі довгі нитки. Кристали неорганічних речовин розташовані між фібрілами і міцно прикріплені до них. Така складна структура визначає механічні властивості кісткової тканини – пружність і пластичність. Модуль пружності кісткової тканини має проміжне значення між модулями пружності її компонентів й істотно залежить від їх процентного вмісту. При експериментальних дослідженнях пружних властивостей кісткової тканини припускають, що кістка має суцільну будову, оскільки розміри структурних елементів набагато менші за саму кістку. Кістка вважається однорідною й ізотропною, що володіє однаковими механічними властивостями в усіх точках і по всіх напрямках. Існують різні методи визначення модуля пружності. В даній роботі модуль пружності визначається з деформації вигину. Якщо на середину прямого пружного стержня, розміщеного на твердих опорах, діє сила
Рис.5
Будова гідравлічного преса
На корпусі преса (див. рис.7), в якому знаходяться великий циліндр з робочим поршнем і малий циліндр з насосом і поршнем, закріплений манометр, розрахований на тиск до 19,6–24,5 МПа (200–250 кгс/см2) та мікрометр переміщення з ціною поділки 0,01 мм, запобіжний клапан і дві колонки з опорною плитою. Позаду корпусу розташовані два вентилі для випуску повітря і зливу масла.
Рис.7. В основі корпусу є бачок для масла місткістю 0,4 л. Нагнітання масла в робочий циліндр здійснюється рукояткою малого поршня. У великому циліндрі (1) рухається поршень (2) з плитою. Поршень щільно підігнаний до циліндра в його верхній частині за рахунок шкіряної прокладки – манжета (3), яка створює ущільнення між стінками циліндра і поршнем. На стінці циліндра знаходиться вентиль (4) для випуску повітря з циліндра. Над поршнем закріплена на двох колонках верхня плита (5). На колонках нанесені кругові поперечні мітки, що показують межу підйому поршня. Малий циліндр (6)з насосом і поршнем (7) служить для нагнітання масла у великий циліндр. Поршень насоса приводиться в рух рукояткою (5). Функції всмоктуючого клапана (9) і нагнітального клапана (10) виконують сталеві кульки. Масло поступає в насос по каналу (11) з бака. З насоса в циліндр масло проходить по каналу (12), закритому з одного боку пробкою (13). Для зливу масла з великого циліндра в бак призначений вентиль (14), для випуску із бака – гайка заглушки (18) і гвинт (17). Порядок виконання роботи 1. Виміряти довжину досліджуваного стержня l. 2. За допомогою штангенциркуля в декількох місцях виміряти товщину b і ширину а стержня і визначити їх середні значення, а також діаметр великого поршня d. Результати занести в таблицю 1. 3. Досліджуваний стержень розмістити на призму нижньої опори підставки. 4. За допомогою ручного преса затиснути досліджуваний об’єкт між призмами верхньої та нижньої опори. 5. За допомогою поворотної шкали мікрометра добитися нульового показу датчика переміщення. 6. Вигнути стержень. При цьому записати покази манометра та датчика переміщень. Добавляючи кожний раз навантаження записувати величину тиску та величину стріли прогину. 7. Побудувати графік залежності стріли прогину λ від тиску р, визначити тангенс кута нахилу 8. Визначити модуль Юнга Е за формулою 9. Визначити відносну похибку вимірювання за формулою:
12. Визначити абсолютну похибку
Таблиця 1- результати вимірювань розмірів досліджуваних стержнів.
Таблиця 2.
Зміст звіту
Формула для розрахунку величини модуля Юнга, графік залежності стріли вигину від прикладеної сили, таблиці результатів, оцінка похибок вимірювань. 5.Контрольні запитання
1. Що таке деформація? Розкажіть про прості види деформації. 2. Наведіть приклади деформацій у людському організмі. (Деформації стиску зазнає хребет, нижні кінцівки і покриви ступні; деформації розтягу – верхні кінцівки, зв’язки, сухожилля, м’язи; згину – хребет, кінцівки, кістки таза; кручення – шия при повороті голови, тулуб у крижах при повороті, кисті рук при обертанні.) 3. Поясніть виникнення сил пружності при різних видах деформацій з врахуванням сил міжмолекулярної взаємодії? 4. Дайте визначення напруги, що виникає в твердому тілі при деформації. Сформулюйте закон Гука. 5. Що таке модуль Юнга? В яких одиницях він визначається? 6. Розкажіть про діаграму напруг. Приведіть приклади крихких і пластичних тіл. Дайте визначення межі міцності. 7. Як визначається модуль пружності в даній роботі. 8. Стоматологи не рекомендують їсти дуже гарячу їжу. Чому? (Різні ділянки зуба мають неоднакові коефіцієнти розширення. При різкому нагрівання зуба в ньому виникають напруження, які можуть спричинити тріщини в емалі). 9. Які речовини відносять до біополімерів? Яка їх роль у життєдіяльності організму? Де вони знаходяться? (Природні біополімери є структурною основою всіх живих організмів і визначають процеси життєдіяльності. До них належать білки, нуклеїнові кислоти (рибонуклеїнова – РНК і дезоксирибонуклеїнова – ДНК), полісахариди. Перші наявні у кожній живій клітині. ДНК знаходяться головним чином у ядрі клітини і відіграє важливу роль, зберігаючи і передаючи по спадковості генетичну інформацію про будову, розвиток та індивідуальні ознаки живого організму.) 10. При відносній легкості кістки здатні протистояти величезним і при цьому різноманітним навантаженням; вони піддаються стиску, розтягу, згину. Удари, стрибки, падіння, аварійні ситуації – в усіх цих випадках наш скелет зазнає хоча й короткочасних, але особливо сильних навантажень і, як правило, витримує їх. Чим пояснюється дивовижна міцність кісток тварин, птахів, людей? (Все це пояснюється дуже раціональною з точки зору механіки будовою кіток. По-перше, міцність і легкість кісток зумовлена їх формою. Завдяки трубчастій формі кістки кінцівок здатні протидіяти величезним стискаючим і згинаючим навантаженням. Наприклад, кульшова кістка людини, поставлена вертикально, витримує вантаж масою 1,5 т. По-друге, слід відзначити особливість внутрішньої будови пустотілих кісток: в них система тонких внутрішніх перемичок орієнтована вздовж напряму можливих механічних напружень, які виникають при тих чи інших деформаціях напруженої кістки. Тому, які б навантаження не прикладалися, кістка ніколи не працює на злам, а тільки на стиск і розтяг.) 11. Діаметр великогомілкової кістки 3,2 см, товщина стінки 3 мм. Розрив кістки відбувся при навантаженні 18 кН. Знайдіть за цими даними руйнуюче напруження і відносну поздовжню деформацію в момент розриву кістки, якщо модуль Юнга кістки 2,3 ГПа. 12. Мешканці древнього Карфагена вважали жіноче волосся найкращим матеріалом для тяжів своїх метальних машин. А соратники Спартака рятувалися від ворога, спускаючись вниз по вертикальній скалі на мотузках, сплетених з волосся. Людський волос витримує вантаж масою 100 г при діаметрі волосини 0,05 мм. Розрахуйте за цими даними межу міцності людської волосини. Який вантаж може витримати коса, сплетена з 200 000 волосин? 13. Що називається в’язкопружністю? Де проявляється ця властивість у живих системах? 14. Які матеріали називають композиційними? В яких випадках у живих тканин переважають пружні, а в яких випадках – в’язкі властивості? (Композиційні – гетерогенні, термодинамічно нерівноважні системи, які складаються з 2 чи більше компонент, які відрізняються за хімічним складом, фізико-хімічними властивостями та розділені в матеріалі чітко вираженою межею. Кожна з компонент вводиться до складу композиційного матеріалу, щоб надати йому потрібні властивості, яких не має жодна з компонент окремо. Комбінуючи об’ємне співвідношення компонент, можна отримати матеріали з наперед заданими характеристиками. Прояв пружних чи в’язких властивостей у композиційних системах залежить від характеру прикладеної до них механічної сили. При тривалій дії (довшій від часу релаксації) переважають в’язкі властивості. Короткочасна дія сили виявляє переважно пружні властивості живої тканини, оскільки реакції її в’язких властивостей не встигають розвинутися. Навіть для кістки закон Гука дійсний тільки при її швидкій деформації. Якщо ж кістка деформується повільно, то проявляється повзучість кісткової тканини.)
Література
1. Мэрион Дж.Б. Общая физика с биологическими примерами. -М.: Высш. шк., 1986. - 624 с. 2. Ессаулова И.А. и др. Руководство к лабораторным работам по медицинской и биологической физике.:М., „Высшая школа”, 1987. 3. І.М.Кучерук, І..Т. Горбачук, П.П. Луцик. Загальний курс фізики. Механіка. Молекулярна фізика і термодинаміка.:Київ, „Техніка”,1999, т.1.С.209-242. 4. Бранков Г. Основы биомеханики.- М.: Мир, 1981. 5. Ємчик Л., Кміт Я. Медична і біологічна фізика.- Львів: Світ, 2003. 6. Медична і біологічна фізика./ За ред. О.В.Чалого. Підручник для студентів вищих медичних закладів освіти ІІІ-ІV рівнів акредитації.- К.: ВІПОЛ, 2005. 7. Ремизов А.Н. Медицинская и биологическая фізика: Учеб. для мед.вузов.- М.: Высшая школа, 1996. 8. Федишин Я.І. Фізика з основами біофізики. Львів: Світ, 2005. 9. Березовский В.А., Колотилов Н.Н. Биофизические характеристики тканей человека. Справочник.- К.: Наукова думка, 1990. 10. Общий курс физиологии человека и животных. В 2 кн.: Кн.1. Физиология нервной, мышечной и сенсорной систем: Учебник для биол. и мед. спец.вузов./ Под ред.. А.Д.Ноздрачева.- М.: Высшая школа, 1991.
ЛАБОРАТОРНА РОБОТА №4 Капілярні явища Існування крайового кута призводить до того, що поблизу стінок посудини спостерігається викривлення поверхні рідини. У вузькій трубці (капілярі) викривленою виявляється вся поверхня, яка приймає форму частини сфери. Якщо рідина змочує стінки, поверхня має ввігнуту форму, якщо не змочує – опуклу. Якщо капіляр занурити одним кінцем в рідину, налиту в широку посудину, то під викривленою поверхнею рідини в капілярі тиск відрізнятиметься від тиску під плоскою поверхнею в посудині на величину | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |


 ,
мм
,
мм
 ,
мм
,
мм
 ,
мм
,
мм
 ,
мм2
,
мм2
 ,
мм
,
мм
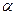
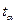
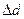 ,
мм
,
мм
 ,
%
,
%
 ,
мм
,
мм
 ,
мм
,
мм
 ,
мм
,
мм
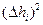 , мм2
, мм2
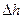 ,
мм
,
мм
 , кг/м3
, кг/м3
 , кг/м3
, кг/м3
 для циліндра згідно формули
для циліндра згідно формули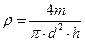 .
. .
. ,
, – часткові похідні функції
– часткові похідні функції  по змінних
по змінних  , відповідно, які взяті при
, відповідно, які взяті при  .
. ,
,  ,
, 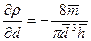 ,
, .
. .
. , та
, та  виміряти не менше трьох разів і результати записати у звітну таблицю №1.
виміряти не менше трьох разів і результати записати у звітну таблицю №1. .
. , то похибка буде знаходитися наступним чином
, то похибка буде знаходитися наступним чином ;
; .
. , а потім похибку ∆g:
, а потім похибку ∆g: .
.





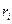



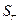











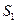 , що відповідає моменту часу
, що відповідає моменту часу  .
. знаходять величину коефіцієнта загасання
знаходять величину коефіцієнта загасання 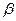 .
. . Дані вимірювань заносять в таблицю №3.
. Дані вимірювань заносять в таблицю №3. , знаходять величину логарифмічного декремента загасання
, знаходять величину логарифмічного декремента загасання  . А далі за формулою (13) знаходять величину коефіцієнта загасання
. А далі за формулою (13) знаходять величину коефіцієнта загасання 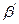 .
. і визначається зі співвідношення
і визначається зі співвідношення  , де
, де  – абсолютний зсув паралельних шарів один відносно одного, а
– абсолютний зсув паралельних шарів один відносно одного, а  – висота тіла, що деформується. Силу
– висота тіла, що деформується. Силу  , що направлена по дотичній до поверхні, на яку вона діє, називають тангенціальною. Позначимо через
, що направлена по дотичній до поверхні, на яку вона діє, називають тангенціальною. Позначимо через 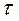 тангенціальну напругу, яка виникає в зразку внаслідок дії тангенціальної сили і розглянемо супроводжуючу її деформацію зсуву. Нехай однорідне тіло має форму прямокутного паралелепіпеда (рис.3). Тоді в будь-якому перерізі, паралельному граням паралелепіпеда, тангенціальна напруга визначається співвідношенням
тангенціальну напругу, яка виникає в зразку внаслідок дії тангенціальної сили і розглянемо супроводжуючу її деформацію зсуву. Нехай однорідне тіло має форму прямокутного паралелепіпеда (рис.3). Тоді в будь-якому перерізі, паралельному граням паралелепіпеда, тангенціальна напруга визначається співвідношенням  , де S – площа грані. Під дією напруги тіло деформується і одна з граней зміститься відносно іншої на деяку відстань
, де S – площа грані. Під дією напруги тіло деформується і одна з граней зміститься відносно іншої на деяку відстань  , де коефіцієнт G називається модулем зсуву і, як і модуль Юнга Е, вимірюється в Паскалях. Модуль Юнга і модуль зсуву повністю визначають механічні властивості однорідного твердого тіла у випадку пружних деформацій і, зокрема, швидкості розповсюдження поздовжніх і поперечних хвиль. (У поздовжніх хвилях у середовищі розповсюджується деформація змінного стиснення і розтягування, а в поперечних – деформація зсуву).
, де коефіцієнт G називається модулем зсуву і, як і модуль Юнга Е, вимірюється в Паскалях. Модуль Юнга і модуль зсуву повністю визначають механічні властивості однорідного твердого тіла у випадку пружних деформацій і, зокрема, швидкості розповсюдження поздовжніх і поперечних хвиль. (У поздовжніх хвилях у середовищі розповсюджується деформація змінного стиснення і розтягування, а в поперечних – деформація зсуву). від відносної деформації
від відносної деформації  при односторонньому розтягуванні. Розглянемо якісно діаграму напруг для металевого зразка (рис.4).
при односторонньому розтягуванні. Розглянемо якісно діаграму напруг для металевого зразка (рис.4). , встановлена Гуком, виконується лише в дуже вузькому діапазоні деформацій (ділянка ОА) до межі пропорційності
, встановлена Гуком, виконується лише в дуже вузькому діапазоні деформацій (ділянка ОА) до межі пропорційності  . Причому для цієї ділянки ОА модуль Юнга чисельно рівний тангенсу кута нахилу кривої. При подальшому збільшенні напруги деформація ще залишається пружною, хоча лінійність кривої порушується, і до межі пружності
. Причому для цієї ділянки ОА модуль Юнга чисельно рівний тангенсу кута нахилу кривої. При подальшому збільшенні напруги деформація ще залишається пружною, хоча лінійність кривої порушується, і до межі пружності  пластичні деформації не виникають (ділянка АВ).
пластичні деформації не виникають (ділянка АВ).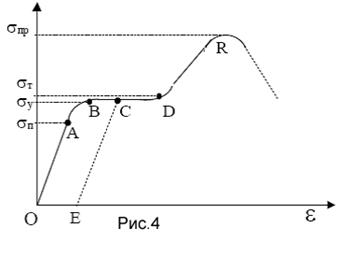
 ), а потім наступає його руйнування.
), а потім наступає його руйнування.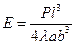
 – навантаження (в ньютонах);
– навантаження (в ньютонах);  ,
,  – відповідно довжина, ширина та висота стержня;
– відповідно довжина, ширина та висота стержня; 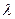 – стріла прогину (в метрах).
– стріла прогину (в метрах). (рис.5), то стержень вигинається. Легко зрозуміти, що при такому вигині верхні шари стержня стискаються, нижні – розтягуються, а деякий середній шар, який називають нейтральним, зберігає довжину і лише зазнає викривлення.
(рис.5), то стержень вигинається. Легко зрозуміти, що при такому вигині верхні шари стержня стискаються, нижні – розтягуються, а деякий середній шар, який називають нейтральним, зберігає довжину і лише зазнає викривлення.

 .
. , де
, де  ,
, 



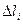






 ,
кг/см2
,
кг/см2
 ,
н
,
н
 ,
Па
,
Па
 ,
Па
,
Па



 ,
Па
,
Па
 , яка визначається згідно формули (1):
, яка визначається згідно формули (1):  , де R – радіус кривизни поверхні. Радіус кривизни можна виразити через крайовий кут і радіус капіляра r. Справді, з рис.3 видно, що
, де R – радіус кривизни поверхні. Радіус кривизни можна виразити через крайовий кут і радіус капіляра r. Справді, з рис.3 видно, що  , а отже,
, а отже, 



