
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Визначення моменту інерції тіла на подвійному підвісі
Визначення моменту інерції тіла на подвійному підвісі
Мета роботи
Визначення моменту інерції тіла стосовно осі, що проходить крізь його центр мас.
Теоретична частина
Момент інерції тіла I стосовно деякої осі – це фізична величина, що являє собою міру інертності тіла під час обертального руху і дорівнює сумі добутків мас У роботі визначають момент інерції тіла правильної форми, яке закріплюється на стрижні так, щоб центри мас тіла і стрижня розміщувалися на одній вертикалі (рис. 9.1). Повернувши стрижень у горизонтальній площині на деякий кут
Рис. 9.1 Рис. 9.2 Якщо стрижень відпустити, то він буде коливатися за гармонічним законом:
де Під час проходження стрижнем стану рівноваги потенціальна енергія системи повністю переходить у кінетичну енергію коливань:
де Зміну висоти центра мас визначимо, розглядаючи систему у двох граничних станах при крутильних коливаннях. Після перетворень знайдемо (рис. 9.1):
Для знаходження максимальної кутової швидкості візьмемо похідну від кута відхилення (9.2) за часом:
Після підстановки h i
Аналогічно для моменту інерції стрижня визначаємо:
Оскільки момент інерції є величиною адитивною (
Експериментальні дослідження
Як видно з рис. 9.1, стрижень підвішений на двох нитках однакової довжини так, що має можливість коливатися в горизонтальній площині. На стрижень можна надівати тіла з отворами, центри яких суміщаються із центром мас стрижня. Під час проведення вимірювань сам стрижень або стрижень з розміщеним на ньому тілом відхиляється на невеликий кут в горизонтальній площині і приводиться у коливальний рух стосовно осі ОО′.
Під час виконання роботи потрібно: 1. Виміряти довжину ниток ℓ і відстані а і b між точками кріплення ниток. Маса стрижня 2. Тіло, що досліджують, помістити на стрижень, сумістивши вісь тіла, стосовно якої визначають момент інерції, з віссю приладу. 3. Виміряти секундоміром час 25 – 50 коливань. Повторити виміри три-чотири рази. Вирахувати період коливань 4. Знявши тіло, повторити виміри за п. 2 для ненавантаженого стрижня і вирахувати період його коливань Обробка результатів вимірювань
1. За формулою (9.8) обчислити момент інерції тіла. 2. Результати вимірювань і обчислень занести в таблицю 9.1.
Таблиця 9.1
Контрольні запитання
1. Що таке момент інерції матеріальної точки? 2. Що таке момент інерції твердого тіла? 3. Які властивості тіла характеризує момент інерції? 4. Який коливальний рух називають гармонічним? 5. За якою формулою можна розрахувати кінетичну енергію тіла, що обертається? 6. Запишіть закон збереження енергії для крутильних коливань стрижня. 7. Чому потрібно, щоб центр мас тіла був на одній вертикалі із центром інерції диска? 8. Які закони збереження виконуються під час крутильних коливань?
Визначення моменту інерції тіла на трифілярному підвісі
Мета роботи
Визначення моменту інерції тіла, яке розміщене на трифілярному підвісі стосовно осі, що проходить крізь його центр мас, і перевірка теореми Штейнера.
Теоретична частина
Момент інерції тіла I – це фізична величина, що являє собою міру інертності тіла під час обертального руху і дорівнює сумі добутків мас
У роботі визначають момент інерції тіла правильної форми, яке розміщене на диску трифілярного підвісу так, щоб центри мас тіла і стрижня лежали на одній вертикалі (рис.10.1). Повернувши диск у горизонтальній площині на деякий кут де Якщо диск відпустити, то він буде коливатись за гармонічним законом:
де
де Зміну висоти центра мас визначимо, розглянувши систему у двох граничних станах під час крутильних коливань. Після перетворень знайдемо (рис. 10.1):
Для знаходження максимальної кутової швидкості візьмемо похідну від кута відхилення (10.2) за часом:
Після підстановки
Аналогічно для моменту інерції диска маємо:
Оскільки момент інерції є величиною адитивною (
Мета роботи
Визначення прискорення вільного падіння за допомогою математичного маятника. Математичним маятником називається матеріальна точка (куля), що підвішена на довгій нерозтяжній нитці. Період коливань математичного маятника залежить від довжини нитки
Із цієї формули можна знайти прискорення вільного падіння, якщо виміряти довжину нитки і період коливань:
Точно виміряти довжину нитки достатньо складно, тому замість довжини
Якщо при довжині нитки
Із цієї формули виведемо робочу формулу:
Мета роботи
Вивчення коливань, що згасають, та визначення коефіцієнта згасання, логарифмічного декременту згасання та добротності системи, яка коливається. Теоретична частина В реальних коливальних системах завжди є сили опору, дія яких призводить до зменшення енергії. Розглянемо вільні коливання, що затухають. При малих швидкостях руху сили опору середовища пропорційні швидкості:
де Знак (–) вказує на те, що сила і швидкість мають протилежний знак. Запишемо рівняння руху системи під дією квазіпружної сили
де Рішення диференційного рівняння (12.2) має вигляд:
де A0 – амплітуда коливань в початковий момент часу, Коливання, що затухають, є неперіодичними, тому що в них ніколи не повторюються максимальні зсуви, швидкості, прискорення. Внаслідок того, що коливальна система проходить крізь положення рівноваги через рівні проміжки часу T, цю величину називають періодом коливань, що згасають:
де Із формули 12.3 випливає, що амплітуда коливань, що згасають, зменшується із часом за законом:
Із формули 12.5 випливає, що коефіцієнт згасання дорівнює натуральному логарифму відношення амплітуд коливань і часу:
Натуральний логарифм відношення амплітуд зсув, що відрізняють-ся на період T, називають логарифмічним декрементом згасання:
Підставивши
Нехай за час t амплітуда зменшилася у еразів. За цей час система робить
Мета роботи
Визначення універсальної газової сталої методом відкачки. Теоретична частина
Універсальну газову сталу
де Всі параметри газу можна виміряти, але газ можна зважити тільки сумісно з посудиною. Тому для знаходження маси газу розглянемо рівняння 13.1 для двох мас
Вивчення властивостей газів Мета роботи
Визначення коефіцієнта в’язкості, довжини вільного пробігу і ефективного діаметра молекул повітря. Теоретична частина
За формулою Пуазейля, об’єм повітря
де З формули 14.1 можна вивести формулу для знаходження коефіцієнта в’язкості повітря:
Для реальних газів (з урахуванням розподілу молекул за швидкостями і сил взаємодії між ними) виводимо формулу, що пов’язує довжину вільного пробігу молекул із середньою арифметичною швидкістю, в’язкістю і густиною повітря
Середня арифметична швидкість молекул газу:
Із рівняння Клапейрона-Менделєєва густина газу
де тиск р ≈ 1 105 Па; Т – абсолютна температура; Якщо виміряти коефіцієнт в’язкості повітря і підрахувати Ефективний діаметр молекул
де n – кількість молекул у одиниці об’єму. Її можна знайти з формули:
де Про характер течії повітря у капілярі можна робити висновки за числом Рейнольдса:
де r – радіус капіляра; Якщо число
Мета роботи
Визначення відношення теплоємності при постійному тиску
Теоретична частина
Теплоємність С – фізична величина, яка дорівнює кількості теплоти для нагрівання тіла на один градус.
Теплоємність одиниці маси речовини називають питомою теплоємністю, а теплоємність одного моля – молярною. Для газів розрізняють теплоємність при постійному тиску і постійному об’ємі. На нагрівання газу при постійному тиску потрібна більша кількість теплоти на величину роботи розширення газу ніж при постійному об’ємі, тому В роботі для визначення відношення теплоємностей де Якщо в балоні відкрити пробку, щоб повітря швидко (адіабатично) розширилося (тиск впаде до атмосферного), то температура повітря у балоні зменшиться. Потім повітря почне прогріватися до кімнатної температури і тиск збільшиться: Перехід повітря з першого стану в другий відбувається адіабатично, тому буде виконуватися співвідношення:
Перехід повітря з першого стану в третій відбувається ізотермічно, тому можна записати:
Замінивши відношення об’ємів відношенням тисків (формули15.4 і 15.5 і взявши логарифм, дістанемо для
Тиск
Тобто відношення теплоємностей можна знайти за формулою:
Мета роботи
Визначення в’язкості рідини методом кульового віскозиметра за методом Стокса. Теоретична частина В’язкість рідини (або газу) – це здатність одного шару рідини протидіяти переміщенню другого шару. В’язкість виникає внаслідок обміну імпульсами між молекулами. За Ньютоном, сила внутрішнього тертя прямо пропорційна градієнту швидкості і площі поверхні S шарів рідини, які стикаються:
де В міжнародній системі одиниць СІ одиниця в’язкості дорівнює: (одиниця в’язкості в абсолютній Гаусовій системі одиниць – пуаз Є більш ніж 15 методів вимірювання в’язкості. Найбільш поширені з них здійснюють з використанням ротаційного, капілярного та кульового віскозиметрів. Ротаційний віскозиметр. Вимірювання в’язкості базується на визначенні швидкості обертання циліндра у в’язкому середовищі. Капілярний віскозиметр. Вимірювання коефіцієнта в’язкості базується на вимірюванні швидкості витікання рідини з циліндричної трубки. В’язкість розраховується за формулою:
де Кульовий віскозиметр. Вимірювання в’язкості базується на визначенні швидкості падіння кульки у в’язкому середовищі. За Стоксом, при повільному русі тіла у в’язкому середовищі між шарами рідини діють сили внутрішнього тертя:
де При сталому падінні кульки в рідині сума сил, які на неї діють, дорівнює нулю (рис.16.1): де сила тяжіння Підставивши у формулу 16.3 значення
де Мета роботи
Визначення коефіцієнта поверхневого натягу рідини за методом відриву кільця на вагах Жоллі. Теоретична частина
Поверхня рідини на межі з повітрям веде себе як пружна плівка. Така поведінка обумовлена силами поверхневого натягу. Під дією сил поверхневого натягу рідина намагається зменшити свою поверхню. Коефіцієнт поверхневого натягу рідини
Поверхневий натяг зменшується у процесі збільшення температури і дорівнює нулю при критичній температурі. Поверхневий натяг розчинів відрізняється від поверхневого натягу чистих розчинників. Наприклад, цукор збільшує поверхневий натяг, а солі знижують. Речовини, що значно зменшують поверхневий натяг, називають поверхнево-активними, або детергентами. До детергентів належать солі жирних кислот (наприклад, мило) і денатуровані білки. Обумовлені силами поверхневого натягу капілярні явища дуже важливі для життєдіяльності рослин, тому що сприяють підйому розчинів поживних речовин по стовбурах рослин. Сили поверхневого натягу важливо знати, вивчаючи дії поверхнево-активних речовин на мембрани клітин, стан біологічно важливих рідин. Визначення моменту інерції тіла на подвійному підвісі
Мета роботи
Визначення моменту інерції тіла стосовно осі, що проходить крізь його центр мас.
Теоретична частина
Момент інерції тіла I стосовно деякої осі – це фізична величина, що являє собою міру інертності тіла під час обертального руху і дорівнює сумі добутків мас У роботі визначають момент інерції тіла правильної форми, яке закріплюється на стрижні так, щоб центри мас тіла і стрижня розміщувалися на одній вертикалі (рис. 9.1). Повернувши стрижень у горизонтальній площині на деякий кут
Рис. 9.1 Рис. 9.2 Якщо стрижень відпустити, то він буде коливатися за гармонічним законом:
де Під час проходження стрижнем стану рівноваги потенціальна енергія системи повністю переходить у кінетичну енергію коливань:
де Зміну висоти центра мас визначимо, розглядаючи систему у двох граничних станах при крутильних коливаннях. Після перетворень знайдемо (рис. 9.1):
Для знаходження максимальної кутової швидкості візьмемо похідну від кута відхилення (9.2) за часом:
Після підстановки h i
Аналогічно для моменту інерції стрижня визначаємо:
Оскільки момент інерції є величиною адитивною (
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 297; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.244.136 (0.01 с.) |
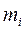 усіх матеріальних точок тіла і квадратів їх відстаней до цієї осі обертання. Центром мас (або центром інерції) тіла називається точка, стосовно якої не відбувається обертання тіла в полі сили тяжіння.
усіх матеріальних точок тіла і квадратів їх відстаней до цієї осі обертання. Центром мас (або центром інерції) тіла називається точка, стосовно якої не відбувається обертання тіла в полі сили тяжіння.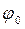 (рис. 9.2), знаходимо, що центр мас тіла зі стрижнем підніметься на величину
(рис. 9.2), знаходимо, що центр мас тіла зі стрижнем підніметься на величину  і її потенціальна енергія збільшиться на величину:
і її потенціальна енергія збільшиться на величину: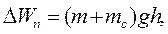 (9.1)
(9.1) де
де  маса тіла;
маса тіла;  маса стрижня.
маса стрижня.
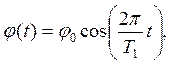 (9.2)
(9.2)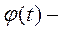 кут відхилення для моменту часу t; період крутильних коливань системи (стрижня і тіла).
кут відхилення для моменту часу t; період крутильних коливань системи (стрижня і тіла).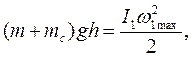 (9.3)
(9.3)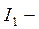 момент інерції системи;
момент інерції системи; 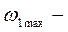 максимальна кутова швидкість в момент проходження стану рівноваги.
максимальна кутова швидкість в момент проходження стану рівноваги.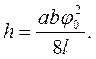 (9.4)
(9.4)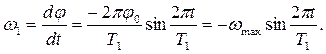 (9.5)
(9.5)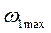 у формулу 9.3 одержимо вираз для моменту інерції системи тіла і стрижня:
у формулу 9.3 одержимо вираз для моменту інерції системи тіла і стрижня: (9.6)
(9.6)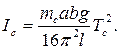 (9.7)
(9.7) ), то з урахуванням формул 9.6 і 9.7 момент інерції тіла визначається за формулою:
), то з урахуванням формул 9.6 і 9.7 момент інерції тіла визначається за формулою: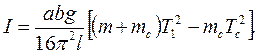 (9.8)
(9.8)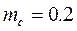 кг, маса тіла m вказана на поверхні.
кг, маса тіла m вказана на поверхні.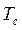 системи.
системи.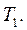
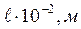
 (10.1)
(10.1) маса диска.
маса диска. (10.3)
(10.3) момент інерції системи;
момент інерції системи; 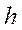 i
i 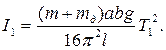 (10.6)
(10.6) (10.7)
(10.7) ), то з урахуванням формул 10.6 і 10.7 момент інерції тіла визначають за формулою:
), то з урахуванням формул 10.6 і 10.7 момент інерції тіла визначають за формулою: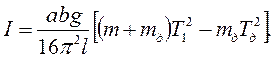 (10.8)
(10.8) і прискорення вільного падіння і не залежить від маси маятника:
і прискорення вільного падіння і не залежить від маси маятника: (11.1)
(11.1)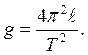 (11.2)
(11.2)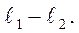
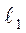 період коливань маятника
період коливань маятника 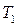 , а при довжині нитки
, а при довжині нитки 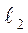 період коливань маятника
період коливань маятника 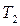 , то:
, то: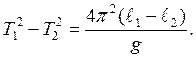 (11.3)
(11.3)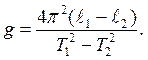 (11.4)
(11.4)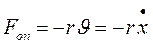 , (12.1)
, (12.1)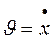 – швидкість руху.
– швидкість руху. при наявності сили опору
при наявності сили опору 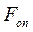 :
: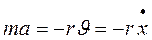 , (12.2)
, (12.2)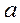 =
= 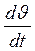 – прискорення системи, що коливається.
– прискорення системи, що коливається.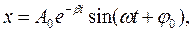 (12.3)
(12.3)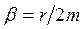 –коефіцієнт згасання,
–коефіцієнт згасання, 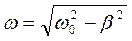 – циклічна частота коливань, що згасають,
– циклічна частота коливань, що згасають,  0 – власна частота коливань системи.
0 – власна частота коливань системи. , (12.4)
, (12.4) - коефіцієнт згасання.
- коефіцієнт згасання. . (12.5)
. (12.5) (12.6)
(12.6)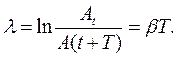 (12.7)
(12.7)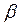 =
= 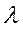 /T у формулу (12.5) матимемо для амплітуди коливань, що згасають:
/T у формулу (12.5) матимемо для амплітуди коливань, що згасають: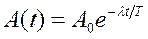 . (12.8)
. (12.8) коливань. З умови
коливань. З умови 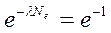 маємо:
маємо: 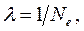 тобто логарифмічний декремент згасання за модулем обернений числу коливань, що здійснюються за час, протягом якого амплітуда коливань зменшується у е разів.
тобто логарифмічний декремент згасання за модулем обернений числу коливань, що здійснюються за час, протягом якого амплітуда коливань зменшується у е разів.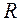 можна визначити з рівняння Клапейрона-Менделєєва:
можна визначити з рівняння Клапейрона-Менделєєва: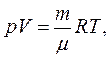 (13.1)
(13.1)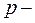 тиск газу;
тиск газу;  об’єм;
об’єм; 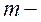 маса газу;
маса газу; 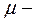 молярна маса газу;
молярна маса газу;  температура.
температура.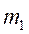 і
і 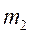 одного газу при однаковому тиску і температурі. Тоді для газової сталої:
одного газу при однаковому тиску і температурі. Тоді для газової сталої: (13.2)
(13.2)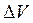 , що проходить крізь капіляр радіуса
, що проходить крізь капіляр радіуса  довжиною
довжиною  , за час t, пропорційний різниці тисків на кінцях капіляра
, за час t, пропорційний різниці тисків на кінцях капіляра 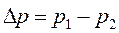 :
: , (14.1)
, (14.1)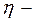 в’язкість газу.
в’язкість газу.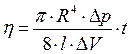 . (14.2)
. (14.2)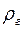 :
: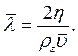 (14.3)
(14.3)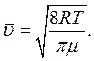 (14.4)
(14.4)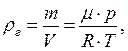 (14.5)
(14.5) – молярна маса газу (для повітря М = 29.10-3 кг/моль).
– молярна маса газу (для повітря М = 29.10-3 кг/моль).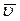 і
і  .
.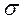 можна підрахувати за формулою для довжини вільного пробігу:
можна підрахувати за формулою для довжини вільного пробігу:
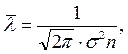 (14.6)
(14.6) (14.7)
(14.7)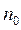 = 2,7 1025– число Лошмідта – кількість молекул в одиниці об’єму при нормальних умовах (р0 = 1.01.105 м-3 і T0 = 273К).
= 2,7 1025– число Лошмідта – кількість молекул в одиниці об’єму при нормальних умовах (р0 = 1.01.105 м-3 і T0 = 273К).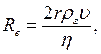 (14.8)
(14.8)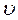 – середня швидкість течії.
– середня швидкість течії.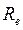 менше 2000, то потік ламінарний, а якщо більше 2600 – турбулентний. При значеннях 2000 – 2600 потік може бути як ламінарним, так і турбулентним.
менше 2000, то потік ламінарний, а якщо більше 2600 – турбулентний. При значеннях 2000 – 2600 потік може бути як ламінарним, так і турбулентним.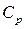 до теплоємності при постійному об’ємі
до теплоємності при постійному об’ємі  і порівняння результату вимірювань з теоретичним значенням.
і порівняння результату вимірювань з теоретичним значенням. (15.1)
(15.1)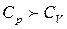 . Відношення
. Відношення  відіграє важливу роль під час опису процесів у газах. Так, у рівнянні Пуассона воно є показником адіабати. Від величини
відіграє важливу роль під час опису процесів у газах. Так, у рівнянні Пуассона воно є показником адіабати. Від величини  залежитьшвидкість звуку в газах.
залежитьшвидкість звуку в газах.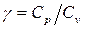 використовують метод Клемана-Дезорма. Цей метод базується на порівнянні зміни тиску газу під час ізотермічної і адіабатичної змініи його об’єму. За допомогою насосу в балон швидко накачують повітря до деякого тиску
використовують метод Клемана-Дезорма. Цей метод базується на порівнянні зміни тиску газу під час ізотермічної і адіабатичної змініи його об’єму. За допомогою насосу в балон швидко накачують повітря до деякого тиску 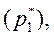 що більший атмосферного
що більший атмосферного  (тиск у мм водяного стовпа). Під час адіабатичного стискування повітря температура в балоні збільшується. Через деякий час у результаті теплового обміну з навколишнім середовищем повітря у балоні охолоджується до кімнатної температури і тиск стабілізується до значення:
(тиск у мм водяного стовпа). Під час адіабатичного стискування повітря температура в балоні збільшується. Через деякий час у результаті теплового обміну з навколишнім середовищем повітря у балоні охолоджується до кімнатної температури і тиск стабілізується до значення: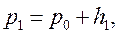 (15.2)
(15.2)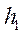 – надмір тиску над атмосферним (виміряється водяним манометром).
– надмір тиску над атмосферним (виміряється водяним манометром).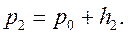 (15.3)
(15.3)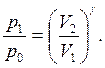 (15.4)
(15.4) (15.5)
(15.5)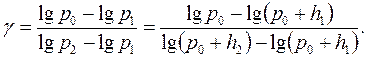 (15.6)
(15.6)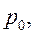
 і
і 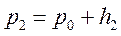 незначно відрізняються, тому логарифми можна замінити їх числовими значеннями:
незначно відрізняються, тому логарифми можна замінити їх числовими значеннями: (15.7)
(15.7)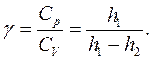 (15.8)
(15.8)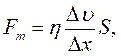 (16.1)
(16.1)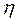 – коефіцієнт внутрішнього тертя або в’язкості.
– коефіцієнт внутрішнього тертя або в’язкості.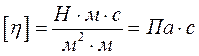
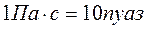 .
. (16.2)
(16.2)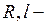 радіус і довжина трубки;
радіус і довжина трубки; 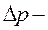 різниця тиску на кінцях трубки;
різниця тиску на кінцях трубки; 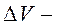 об’єм рідини, яка витікає за час
об’єм рідини, яка витікає за час 

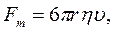 (16.3)
(16.3) радіус кульки;
радіус кульки; 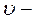 швидкість руху кульки відносно рідини.
швидкість руху кульки відносно рідини.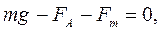 (16.4)
(16.4)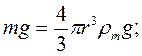 сила Архімеда
сила Архімеда 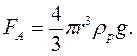
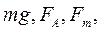 знайдемо
знайдемо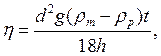 (16.5)
(16.5)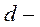 діаметр кульки;
діаметр кульки;  висота та час падіння кульки.
висота та час падіння кульки.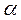 можна визначити як енергію, що потрібна для збільшення площі поверхні рідини на одиницю:
можна визначити як енергію, що потрібна для збільшення площі поверхні рідини на одиницю: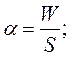
 (17.1)
(17.1)


