Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод Стокса визначення коефіцієнта в’язкості рідиниСодержание книги
Поиск на нашем сайте Сила внутрішнього тертя виникає як під час руху рідини відносно твердого тіла, яке знаходиться в стані спокою, так і під час руху твердого тіла відносно рідини, яка знаходиться в стані спокою. Остання ситуація використовується при вимірюванні коефіцієнту в'язкості методом Стокса. В'язкість рідини поряд з іншими чинниками (форма тіла, умови обтікання тощо) визначає силу опору, яка діє на тіло, що рухається в цій рідині. На кульку, яка рухається у рідині, буде діяти сила опору, яка залежить від в'язкості рідини – η, радіусу кульки – r та швидкості її руху
Важливим є те, що ця формула отримана за умови ламінарного обтікання кульки, тобто такого, при якому шари рідини можна вважати паралельними один одному. Такі умови практично виконуються при досить малих швидкостях руху кульки. Якщо ця умова не виконується, то в рідині утворюються турбулентності і тоді в'язкість, як властивість рідини, втрачає зміст. Для оцінки ламінарності існує спеціальний критерій – число Рейнольдса. За критичне значення числа Рейнольдса для руху кульки в рідині приймають ReКР=10. Метод Стокса для визначення в'язкості полягає у вимірюванні швидкості падіння кульки, яка встановилася сталою, в досліджуваній рідині. Очевидно, що на кульку радіусу r (об'ємом сила тяжіння виштовхуюча сила Архімеда сила Стокса (сила опору рідини)
Рис.2. Сили, які діють на кульку, що падає в рідині.
Сила Стокса залежить від швидкості, тому вона буде зростати при падінні кульки, а отже, буде зростати і сила опору рідини. Цей ріст буде тривати доти, поки сила Стокса не зрівноважить суму сил тяжіння і Архімеда. У випадку такої рівноваги швидкість кульки припинить змінюватися і вона буде продовжувати рух з певною сталою швидкістю. Отже, при усталеному русі кульки рівнодійна всіх сил, які діють на кульку, буде рівна нулю:
або за проекціями Використавши формули (5-7), співвідношення (8) перепишемо у вигляді:
Розв'язавши (9) відносно η, отримаємо наступний вираз:
Використовуючи цю формулу, можна обчислити в´язкість рідини, якщо виміряна швидкість усталеного руху кульки. Вираз (10) справедливий лише тоді, коли кулька падає в безмежному середовищі. Якщо кулька падає уздовж осі трубки радіуса r0, то необхідно враховувати вплив бічних стінок. Виправлення у формулі Стокса для такого випадку теоретично обґрунтував Ладенбург. Формула для визначення коефіцієнта в'язкості з урахуванням виправлень приймає наступний вигляд:
Опис приладів
І) В досліді використовується скляний циліндр із рідиною, в'язкість якої потрібно визначити, із двома мітками, розташованими одна від одної на відстані h (рис.3). Положення верхньої (hв) і нижньої (hн) мітки відраховують по шкалі. Таким чином, похибки Δ hв= Δ hн =Δ h =1 мм. Циліндр закритий втулкою з просвердленим по її осі каналом. Кулька, поміщена в канал, падає уздовж осі циліндра. На дно циліндра опущена сітка С, за допомогою якої витягаються кульки, що впали на дно. Рис. 3. Установка для вимірювання динамічної в´язкості методом Стокса. ІІ) Для вимірювання часу використовують електронний секундомір, систематична похибка якого визначається за формулою: Δ t =0,01(1+ t). в) Мікрометр і штангенциркуль служать для вимірювання діаметрів кульки і циліндра. г) Масштабна лінійка служить для виміру шляху, пройденого кулькою, ціна поділки – 1 мм. д) Термометр, який знаходиться в лабораторії, його точність – 0,1°С.
Порядок виконання роботи 1. Заповнюють скляний циліндр досліджуваною рідиною (гліцерин, касторове чи трансформаторне масло тощо). 2. За допомогою мікрометра визначають діаметр кульки d. 3. За допомогою штангенциркуля визначають діаметр циліндра do. 4. Вибирають верхню мітку hв на циліндрі на кілька сантиметрів нижче рівня рідини, щоб до того моменту, коли кулька буде проходити повз неї, рух її був уже усталеним. Вибирають положення нижньої мітки hн. Виміряють масштабною лінійкою відстань h = hв – hн між мітками на циліндрі. 5. Визначають час падіння кульки t між мітками на циліндрі, орієнтуючи її рух по центру циліндра. При спостереженні за падінням кульки око потрібно розташовувати на рівні верхньої, а потім нижньої мітки, щоб уникнути явища паралакса. Розраховують швидкість усталеного руху кульки за формулою:
6. За показами кімнатного термометра визначають температуру рідини. Виміри проводять з п'ятьма кульками. 7. Результати вимірів заносять у таблицю 1. 8. Розраховують величину коефіцієнту в'язкості рідини за формулою:
Таблиця 1. Визначення коефіцієнту в'язкості.
Густина матеріалу кульки ρк =_______ кг/м3. Густина рідини ρрід =_______ кг/м3. Прискорення сили тяжіння 9,8 м/с2. Обробка результатів 1. Визначити радіуси кульок: r=d/2. Визначити радіус циліндра: rо=dо/2. 2. Розрахувати Δ r, Δ t. Результати занести в таблицю. 3. Обчислити коефіцієнт внутрішнього тертя рідини η за формулою:
4. Визначити відносну похибку:
5. Визначити абсолютну похибку: 6. Записати кінцевий результат у вигляді: 7. Порівняти отриманий результат з табличним значенням. Зміст звіту Формули для розрахунку густини, звітна таблиця, оцінка похибок вимірювань. 6. Контрольні питання 1. Що називається в'язкістю рідини? Який механізм внутрішнього тертя в рідинах з погляду молекулярно-кінетичної теорії? 2. Який фізичний зміст коефіцієнта внутрішнього тертя? Що називається коефіцієнтом кінематичної і динамічної в'язкості? Як динамічна в'язкість пов'язана з кінематичною? 3. Яка залежність в'язкості рідини від температури? Чим пояснюється ця залежність? 4. Чому дорівнює сила в'язкого тертя між двома шарами рідини? 5. Чому швидкість течії в'язкої рідини різна в різних точках перетину потоку? Що таке градієнт швидкості? 6. Яка течія рідини називається ламінарною? Турбулентною? Приведіть приклади турбулентної течії. 7. Запишіть формулу Стокса. За яких умов вона виконується? 8. Які сили діють на кульку, що падає в рідині? Запишіть вираз для цих сил. Чому вимір часу падіння кульки починають не від поверхні рідини, а від мітки на циліндрі, яка достатньо віддалена від поверхні рідини? 9. Як змінюється швидкість падаючої кульки в рідині з часом? Як будуть відрізнятися швидкості, що установилося, для руху кульок різного радіусу? Чому? Література
1. Б.Т.Агапов, Г.В.Максютин, П.И.Островерхов. Лабораторный практикум по физике. – М: Высшая школа, 1982. 2. Л.Ємчик, Я.Кміт. Медична біофізика. – Львів: Місіонер, 1998. 3. Медична і біологічна фізика./ За ред. О.В.Чалого. Підручник для студентів вищих медичних закладів освіти ІІІ-ІV рівнів акредитації.- К.: ВІПОЛ, 2005. 4. Ремизов А.Н. Медицинская и биологическая фізика: Учеб. для мед.вузов.- М.: Высшая школа, 1996. 5. Федишин Я.І. Фізика з основами біофізики. Львів: Світ, 2005.
ЛАБОРАТОРНА РОБОТА №6
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 1458; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.007 с.) |

 . Вираз для сили опору середовища, в якому рухається кулька, вперше була отримана Стоксом і має такий вигляд:
. Вираз для сили опору середовища, в якому рухається кулька, вперше була отримана Стоксом і має такий вигляд: . (4)
. (4) ), яка падає у в'язкому середовищі, діють такі сили (див. рис. 4):
), яка падає у в'язкому середовищі, діють такі сили (див. рис. 4): ;(5)
;(5)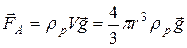 ; (6)
; (6) . (7)
. (7)
 ,
, . (8)
. (8) . (9)
. (9)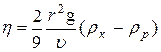 . (10)
. (10) . (11)
. (11)
 .
. . (12)
. (12) .
. .
.