
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Загальні уявлення про статистику, короткі відомості з історії.Содержание книги
Поиск на нашем сайте ЗАГАЛЬНІ УЯВЛЕННЯ ПРО СТАТИСТИКУ, КОРОТКІ ВІДОМОСТІ З ІСТОРІЇ. “ Статистика” – від латинського слова “status” - положення, стан явищ Від кореня цього слова утворилось італійське слово “stato” – держава Осіб, що володіли знаннями про устрій і стан справ у різних державах, політиків називали “ statista ” Від цього ж кореня утворився іменник “s tatistika ”. В науковий ужиток слово “статистика” увійшло у XVIII ст. і первісно вживалось у значенні “державознавсто”. Існували 2 течії політичні арифметики (В. Петі, Дж. Граунд (англійська школа)), які визначали кількісну і якісну сторони статистики. Термін статистика в 1746р. ввели німецький вчений-філософ Генріх Авенхаль, саме він давав визначення статистики, як «державознавство». Історично розвиток статистики пов’язаний з утворенням держав. Уже в країнах Стародавнього світу склалися системи державного та адміністративного обліку. Про це свідчить, зокрема, і Біблія, де у Четвертій книзі Мойсея «Числа» розповідається про облік чоловічого населення, здатного носити зброю. Середньовіччя залишило унікальну пам’ятку — «Книгу страшного суду», в якій зведено дані перепису населення Англії та його майна. Поступово збирання даних про масові суспільні явища ставало регулярним. Розвиток бухгалтерського обліку та первинної реєстрації фактів, нагромадження масових даних і необхідність їх узагальнення, підвищення попиту на інформацію — ось ті чинники, що сприяли формуванню статистики як науки. З розвитком математики, передусім теорії ймовірностей, удосконалювалися методи статистичного аналізу і розширювалась сфера їх використання. У ХХ ст. статистичні методи почали застосовуватися майже в усіх галузях знань. Сьогодні статистику використовують, вивчаючи життєвий рівень населення та громадську думку, оцінюючи підприємницькі та фінансові ризики, у маркетингових дослідженнях, страхуванні тощо. Нині під терміном “статистика” розуміють: 1. Цифри, які характеризують рівні, розміри та обсяги тих або інших суспільних явищ 2. Статистична практика діяльність, спрямована на збирання, нагромадження, обробку та аналіз даних, які характеризують явища суспільного життя; 3. Самостійна суспільна наука, яка займається розробкою методів збирання, зведення, обробки, аналізу даних про явища суспільного життя Статистика як наука. Предмет статистики. Статистика – це наука яка вивчає кількісну сторону масових суспільних, соціально-економічних та інших явищ у їх нерозривному зв’язку з якісною стороною в певних умовах місця та часу. Предмет статистики – кількісна та якісна сторона масових суспільних явищ. Об’єкт статистики – людське суспільство, явища і процеси суспільного життя. Нині під терміном “статистика” розуміють: 1. Цифри, які характеризують рівні, розміри та обсяги тих або інших суспільних явищ 2. Статистична практика діяльність, спрямована на збирання, нагромадження, обробку та аналіз даних, які характеризують явища суспільного життя; 3. Самостійна суспільна наука, яка займається розробкою методів збирання, зведення, обробки, аналізу даних про явища суспільного життя Об’єктами статистичного аналізу можуть бути найрізноманітніші явища й процеси суспільного життя. Предметом статистики є розміри і кількісні співвідношення між масовими суспільними явищами, закономірності їх формування, розвитку, взаємозв’язку.
Методологічна база статистики. Основні розділи статистично науки. Статистична методологія — це комплекс спеціальних, притаманних лише статистиці методів і прийомів дослідження. Вона ґрунтується на загальнофілософських (діалектична логіка) і загальнонаукових (порівняння, аналіз, синтез) принципах. Принципи: 1. Загальнолюдські; 2. Загальнонаукові; Функції: 1. Пізнавальна; 2. Контрольно-організаційна; 3. Керуюча Методологічна база статистики: 1. Теорія пізнання; 2. Діалектична логіка, загальнонаукові прийоми аналізу і синтезу; 3. Системний підхід 4. Основи економічної теорії; 5. Специфічні методи. Особливості статистичної методології пов’язані, по-перше, з точним вимірюванням і кількісним описуванням масових суспільних явищ; по-друге, з використанням узагальнюючих показників для характеристики об’єктивних статистичних закономірностей. Статистика — багатогалузева наука. Вона складається з окремих самостійних розділів, які водночас тісно пов’язані між собою. Виокремлюють чотири складові цієї науки. 1. Теорія статистики розглядає категорії статистичної науки, а також спільні для будь-яких масових явищ методи й засоби аналізу. 2. Економічна статистика вивчає явища і процеси, що відбуваються в економіці, розробляє систему економічних показників та методи вивчення економіки країни чи регіону як єдиного цілого. 3. Галузеві статистики (промислова, фінансова, соціальної інфраструктури і т. ін.) розробляють зміст і методи обчислення показників, які відбивають особливості кожної окремої галузі. 4. Соціальна статистика вивчає соціальні умови та характер праці, рівень життя, прибутків, споживання матеріальних благ і послуг населенням.
Основні поняття в статистиці: статистична сукупність, статистична закономірність, статистичний показник, закон великих чисел. Статистичним показником називають узагальнену числову характеристику будь-якого масового явища в поєднанні з його якісною визначеністю в конкретних умовах місця і часу. Одиниці вимірювання статистичних показників: 1. натуральні (кг, т, м, км та ін.); 2. вартісні (грн.); 3. умовно-натуральні (калоріях, умовні банки та ін.). Статистична сукупність – це певна множина елементів поєднаних умовами існування і розвитку Закономірність – повторюваність, послідовність і порядок у масових процесах Системні властивості сукупності становлять суть статистичних закономірностей, які об’єднуються в 4 групи: 1. Закономірності розвитку (динаміки) явищ. Так, статистика свідчить про збільшення кількості населення Земної кулі, зростання тривалості життя, зменшення середнього віку одруження тощо. 2. Закономірності розподілу елементів сукупності. Це може бути розподіл населення за віком, сімей — за кількістю дітей, комерційних банків — за статутним фондом. 3. Закономірності структурних зрушень. Прикладом може бути збільшення частки міського населення в загальній його кількості, збільшення частки населення похилого віку в сільській місцевості. 4. Закономірності зв’язку між явищами. Наприклад, залежність продуктивності праці від фондоозброєності, собівартості продукції — від продуктивності праці, урожайності — від родючості ґрунту, попиту — від ціни на товар. Статистичним еквівалентом властивостей, притаманних елементам сукупності, є ознака. Кожний елемент сукупності характеризується багатьма ознаками, значення яких змінюються від елемента до елемента або від одного періоду до іншого. Ознака, яка набуває в межах сукупності різних значень, називається такою, що варіює, а відмінність, коливання значень ознаки — варіацією. Одні ознаки виражаються числами, інші — словесно. Їх називають відповідно кількісними і атрибутивними (описовими). Серед атрибутивних ознак одні чітко окреслені (стать, професія, галузь), інші невизначені (суб’єктивні оцінки, твердження, думки). За характером варіації ознаки метричної шкали поділяються на дискретні та неперервні. Дискретні ознаки мають лише окремі цілочислові значення: кількість укладених на біржі угод, кількіcть дітей у сім’ї тощо. Неперервні ознаки мають будь-які значення в певних межах варіації.
Відносні величини динаміки В.В. Динаміки – характеризує напрям та інтенсивність зміни показника в часі і визначається співвідношенням його значень за періоди або моменти часу. Існує 2 способи обчислення відносних величин динаміки: - Базисний – кожний наступний показник порівнюється з попереднім показником, який приймається за базу. - Ланцюговий – кожен наступний порівнюється з попереднім. Відносний показник виконання плану – відношення фактично осягнутого рівня до планового завдання (факт до плану).
Ув. пл. = У1/Упл Відносний величина планового завдання – відношення величини показника встановленого на плановий період до його величини досягнутої за попередній період. (план до факту попереднього періоду). Упл. завд = Упл / У0 (план, стандарт, еталон)
Відносні величини структури Статистичні сукупності структуровані, у них завжди можна виявити певні складові. Відносні величини структури характеризують склад, структуру сукупності за тією чи іншою ознакою. Вони визначаються відношенням розмірів складових частин сукупності до загального підсумку. Скільки складових, стільки відносних величин структури. Кожну з них окремо називають часткою, або питомою вагою, виражають простим чи десятковим дробом або процентом. За допомогою відносних величин структури можна оцінити структурні зрушення, тобто зміни у складі сукупності за певний період часу. Така оцінка ґрунтується на порівнянні часток dj за два періоди. У стр = fi / Sfi Середня арифметична Оскільки для більшості соціально-економічних явищ характерна адитивність обсягів (виробництво цукру, витрати палива тощо), то найпоширенішою є арифметична середня, яка обчислюється діленням загального обсягу значень ознаки на обсяг сукупності. За первинними, незгрупованими даними обчислюється середня арифметична проста:
У великих за обсягом сукупностях окремі значення ознаки (варіанти) можуть повторюватись. У такому разі їх можна об’єднати в групи (j = 1, 2,..., m), а обсяг значень ознаки визначити як суму добутків варіант хj на відповідні їм частоти fj, тобто як
Вагами можуть бути частоти або частки (відносні величини структури), іноді інші величини (абсолютні показники). Середня не збігається з жодним значенням ознаки, але це типовий рівень кваліфікації налагоджувачів фірми. Формально між середньою арифметичною простою і середньою арифметичною зваженою немає принципових відмінностей. Адже багаторазове (f раз) підсумовування значень однієї варіанти замінюється множенням варіант х на вагу f. Проте функціонально середня зважена більш навантажена, оскільки враховує поширеність, повторюваність кожної варіанти і певною мірою відображує склад сукупності. Значення середньої зваженої залежить не лише від значень варіант, а й від структури сукупності. Чим більшу вагу мають малі значення ознаки, тим менша середня, і навпаки. Наприклад, незважаючи на той факт, що в двох регіонах мешкають люди різного віку, у тому регіоні, де більше дітей, середній вік населення буде менший. На цю властивість середніх слід зважати при використанні їх у порівняльному аналізі сукупностей, склад яких істотно різний. У таких випадках, аби елімінувати (усунути) вплив структури сукупності на середню, вдаються до пошуку стандартизованих ваг. У структурованій сукупності при розрахунку середньої зваженої варіантами можуть бути як окремі значення ознаки, так і групові середні
Обчислену так середню на відміну від групових називають загальною. Середня арифметична має певні властивості, які розкривають її суть. 1. Алгебраїчна сума відхилень окремих варіант ознаки від середньої дорівнює нулю:
тобто в середній взаємно компенсуються додатні та від’ємні відхилення окремих варіант. 2. Сума квадратів відхилень окремих варіант ознаки від середньої менша, ніж від будь-якої іншої величини:
3. Якщо всі варіанти збільшити (зменшити) на одну й ту саму величину А або в А раз, то й середня зміниться аналогічно. Аналітичні можливості центрованого середнього балу ширші, ніж середньозваженого. Центрований бал може бути додатною чи від’ємною величиною. Знак свідчить про позитивну чи негативну оцінку явища. За допомогою центрованого балу можна порівняти оцінки різних явищ незалежно від розмірності шкали. Для такого порівняння можна скористатися формулою переходу від середньозваженого до центрованого балу:
4. Значення середньої залежить не від абсолютних значень ваг, а від пропорцій між ними. При пропорційній зміні всіх ваг середня не зміниться. Згідно з цією властивістю замість абсолютних ваг — частот fj — можна використати відносні ваги у вигляді часток
Аналітичні показники РД. При вивченні інтенсивності розвитку сусп-екон.явищ в часі широко використовуються такі показники: 1.Абсолютний приріст (D)-різниця між рівнями РД.Цей показник хар-зує наскільки одиниць виміру самого показника збільшився чи зменшився наступний рівень РД по відношенню до якогось попереднього. Dл=У(і)-У(і-1) Dб=У(і)-У(1) Dкб=У(n)-У(1) 2.Коеф-т росту(зростання) Кр-співвідношення рівнів ряду, яке показує в скільки разів наступний рівень > чи < від якогось попереднього. Кл=У(і)/У(і-1) Кб=У(і)/У(1) Ккб=У(n)/У(1) Помноживши коеф-т росту на 100% отримаємо темп росту(зростання). Тр=Кр*100% 3.Коеф-т приросту (Кприр) – цей показник можна визначити т.ч.: а )Кприр=Кр-1 б)Кприр=D(і)/У(і-1), тобто відношенню абсолютного прирісту до базисного рівня. Помноживши коеф-т прирісту на 100% отримаємо темп приросту. Тприр=Кприр*100%. 4.Абсолютне значення 1% приросту -А%-хар-зує вагомість 1% в одиницях виміру показника, зміна якого вивчається в часі. Обчислюються т.ч.: а)А%=Dл/Тприр.л. б)А%=У(і-1)/100 Узагальнюючі хар-ки РД. При вивченні дінаміки рівнів сусп-екон.явищ часто доводиться користуватись узагальнюючими хар-ками, тобто середнім значенням аналітичних показників динаміки, такими є: 1.Середній рівень динаміки (`У¯). Методика обчислення цього показника залежить від виду РД та від наявної інф-ції. Середній рівень періодичного ряду обчислюється за формулою середньої арифметичної простої :`У¯=åУі/n, де Уі-число рівнів ряду. Середній рівень моментного РД обчис-ся за середньою хронологічною, якщо відрізки часу між моментами однакові або за середньою арифметичною і зваженою, якщо відрізки часу різні: ` У¯=(У1/2+У2+У3+…+У(n-1)+Уn/2)/n-1, [хронологічна] де У1 і Уn початковий та кінцевий рівні ряду, n-число рівнів ряду. ` У¯=(å`У¯(і)t(і))/åt(i) [арифметична зважена],`У¯і-середні рівні РД за окремі проміжки часу, які знах-ся як напівсума рівнів на початок і кінець періоду,t(i)-тривалість періоду. 2.Середній абсолютний приріст (Δ¯) Він обчис-ся за формлою середньої арифметичної простої: Δ¯=∑Δ(і)/n, де Δ-ланцюгові абсолютні прирости, n-число цих приростів. Δ¯=(Уn-У1)/(n-1), де У1, У2-початковий та кінцевий рівні ряду, n-число рівнів ряду. 3.Середній коеф-т росту(К¯) -обч-ся за ф-лою середної геометричної. ¯ К=(n)√К1*К2*…*Кn, де К1,К2,Кn-ланцюгові коеф-ти росту, n-їх число. Знаючи, що добуток ланцюгових коеф-тів росту=кінцевому базисному коеф-ту росту, розрахунок середнього коеф-ту можна представити і так: ¯К=(n-1)√Уn/У1, де Уn/У1-Ккб, n-число рівнів ряду.
Таблиця 8.1 ЗІМКНЕННЯ ДИНАМІЧНИХ РЯДІВ
Другий спосіб ґрунтується на співвідношенні квітневих рівнів: 55: 50 = 1,1. Помноживши рівні першого ряду на цей коефіцієнт, дістанемо єдиний зімкнений (порівнянний) ряд динаміки за весь період (остання графа таблиці). Розрахунок характеристик динаміки ґрунтується на порівнянні рівнів ряду. При порівнянні певної множини послідовних рівнів база порівняння може бути постійною чи змінною. За постійну базу вибирається або початковий рівень ряду, або рівень, який уважається вихідним для розвитку явища, що вивчається. Характеристики динаміки, обчислені відносно постійної бази, називаються базисними. Якщо кожний рівень ряду
Таблиця 9.3 ДО РОЗРАХУНКУ СЕРЕДНЬОЗВАЖЕНИХ ІНДЕКСІВ
Умовний торговий оборот
У такому разі зведені індекси за Ласпересом обчислюються як середня арифметична з вагами
Обчислимо середньозважені індекси цін
середньозважений індекс цін
середньозважений індекс фізичного обсягу продажу
Як бачимо, значення середньозважених індексів такі самі, як і відповідних їм агрегатних (див. підрозд. 9.3). При побудові середньозважених індексів вартісні ваги можна замінити відносними величинами структури d, сума яких
Ці формули підтверджують залежність значення зведеного індексу від динаміки окремих складових і пропорцій у сукупності агрегованих елементів. Наприклад, у регіоні виробництво споживчих товарів зменшилось: продовольчих — на 3, непродовольчих — на 7%, а ціни зросли відповідно на 4 і 6%. Унаслідок нерівномірності динаміки виробництва по групах споживчих товарів змінилась їх структура: на 2 п. п. зросла частка продовольчих товарів і на стільки ж зменшилась частка непродовольчих. Розрахунки зведених індексів фізичного обсягу та цін наведено в табл. 9.4.
Таблиця 9.4 ДО РОЗРАХУНКУ СЕРЕДНЬОЗВАЖЕНИХ ІНДЕКСІВ
Зведений індекс фізичного обсягу виробництва Iq = 0,97 × 0,60 + + 0,93 × 0,40 = 0,954 тобто в середньому обсяги виробництва зменшилися на 4,6%. Зведений індекс цін
Середньозважені індекси мають перевагу перед агрегатними, адже за їхньою допомогою можна вишикувати ієрархію індексів від індивідуальних на окремі товари через групові (субіндекси) до загального по всій сукупності елементів. Проте їм властиві й недоліки. Якщо динаміка окремих складових сукупності протилежна, то зведений індекс не в змозі адекватно відобразити закономірність динаміки. Окрім того, середньозважений індекс визначається лише стосовно порівнянного кола елементів. Якщо ж окремі елементи сукупності відсутні в базисному чи поточному періоді, то розрахунок індивідуальних індексів неможливий. У цьому разі перевага надається індексу агрегатної форми. Отже, за кожним індексом стоїть певне економічне явище, що зумовлює методику його розрахунку та змістовність.
Таблиця 22. ЗАГАЛЬНІ УЯВЛЕННЯ ПРО СТАТИСТИКУ, КОРОТКІ ВІДОМОСТІ З ІСТОРІЇ. “ Статистика” – від латинського слова “status” - положення, стан явищ Від кореня цього слова утворилось італійське слово “stato” – держава Осіб, що володіли знаннями про устрій і стан справ у різних державах, політиків називали “ statista ” Від цього ж кореня утворився іменник “s tatistika ”. В науковий ужиток слово “статистика” увійшло у XVIII ст. і первісно вживалось у значенні “державознавсто”. Існували 2 течії політичні арифметики (В. Петі, Дж. Граунд (англійська школа)), які визначали кількісну і якісну сторони статистики. Термін статистика в 1746р. ввели німецький вчений-філософ Генріх Авенхаль, саме він давав визначення статистики, як «державознавство». Історично розвиток статистики пов’язаний з утворенням держав. Уже в країнах Стародавнього світу склалися системи державного та адміністративного обліку. Про це свідчить, зокрема, і Біблія, де у Четвертій книзі Мойсея «Числа» розповідається про облік чоловічого населення, здатного носити зброю. Середньовіччя залишило унікальну пам’ятку — «Книгу страшного суду», в якій зведено дані перепису населення Англії та його майна. Поступово збирання даних про масові суспільні явища ставало регулярним. Розвиток бухгалтерського обліку та первинної реєстрації фактів, нагромадження масових даних і необхідність їх узагальнення, підвищення попиту на інформацію — ось ті чинники, що сприяли формуванню статистики як науки. З розвитком математики, передусім теорії ймовірностей, удосконалювалися методи статистичного аналізу і розширювалась сфера їх використання. У ХХ ст. статистичні методи почали застосовуватися майже в усіх галузях знань. Сьогодні статистику використовують, вивчаючи життєвий рівень населення та громадську думку, оцінюючи підприємницькі та фінансові ризики, у маркетингових дослідженнях, страхуванні тощо. Нині під терміном “статистика” розуміють: 1. Цифри, які характеризують рівні, розміри та обсяги тих або інших суспільних явищ 2. Статистична практика діяльність, спрямована на збирання, нагромадження, обробку та аналіз даних, які характеризують явища суспільного життя; 3. Самостійна суспільна наука, яка займається розробкою методів збирання, зведення, обробки, аналізу даних про явища суспільного життя
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 456; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.015 с.) |


 . Такий процес множення у статистиці називають зважуванням, а число елементів сукупності з однаковими варіантами — вагами. Сама назва «ваги» відбиває факт різновагомості окремих варіант. Значення ознаки осереднюються за формулою середньої арифметичної зваженої:
. Такий процес множення у статистиці називають зважуванням, а число елементів сукупності з однаковими варіантами — вагами. Сама назва «ваги» відбиває факт різновагомості окремих варіант. Значення ознаки осереднюються за формулою середньої арифметичної зваженої:
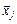 , кожна з яких має відповідну вагу у вигляді групових частот fj:
, кожна з яких має відповідну вагу у вигляді групових частот fj:
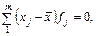


 або процентів 100 dj:
або процентів 100 dj: .
. порівнюється з попереднім
порівнюється з попереднім  , характеристики динаміки називаються ланцюговими.
, характеристики динаміки називаються ланцюговими.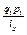
 можна визначити, скоригувавши фактичні обороти індивідуальними індексами цін або фізичного обсягу продажу:
можна визначити, скоригувавши фактичні обороти індивідуальними індексами цін або фізичного обсягу продажу:
 , а індекси за Пааше — як середня гармонічна з вагами
, а індекси за Пааше — як середня гармонічна з вагами 



 .
.
 та фізичного обсягу продажу
та фізичного обсягу продажу  за даними табл. 9.3, використовуючи різні варіанти зважування (
за даними табл. 9.3, використовуючи різні варіанти зважування (
 .
. У цьому разі середньозважені індекси набирають вигляду
У цьому разі середньозважені індекси набирають вигляду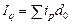 ;
; 

 показує, що ціни в середньому зросли на 4,8%:
показує, що ціни в середньому зросли на 4,8%: .
.


