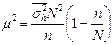Тема 11 Обчислення похибок репрезентативності

Перелік запитань

	Види похибок у вибірковому спостереженні
	Обчислення похибок репрезентативності
	Класи точності та надійності даних

Методичні вказівки

1 Види похибок у вибірковому спостереженні

Для вибіркового обстеження притаманні як похибки реєстрації, так і власні вибіркові похибки (похибки репрезентативності). Проте оскільки вибіркове обстеження передбачає обстеження лише невеликої кількості одиниць, фахівці мають можливість виконати це обстеження більш якісно, знизивши похибки реєстрації. Тому часто вибіркове обстеження може бути більш точним, ніж суцільне.

Статистична характеристика (наприклад, середнє або сумарне значення), обчислена по вибірковій сукупності є оцінкою відповідної характеристики генеральної сукупності. Оскільки вибіркова сукупність не точно відтворює структуру генеральної, то вибіркова оцінка також не збігаються з характеристикою генеральної сукупності.

Приклад. На 10 малих підприємствах працює: 5, 10, 7, 12, 9, 8, 6, 11, 2, 4 працівників. Припустимо, що ми обстежили 5 п-в. = 6,4, = 7,4. Похибка 7,4 - 6,4 = 1.

Розбіжності між ними називаються похибками репрезентативності (власне вибіркові похибки). За причинами виникнення ці похибки поділяються на систематичні (тенденційні) та випадкові. Систематичні похибки репрезентативності виникають за умови, що під час формування вибіркової сукупності порушується принцип випадковості відбору (упереджений відбір елементів, недосконала основа вибірки тощо). Випадкові похибки репрезентативності – це наслідок випадковості відбору елементів сукупності для обстеження. Ці похибки можна визначити за формулами.

Гранична похибка вибірки – це максимально можлива похибка при заданій ймовірності. Визначається за формулою , де – середня похибка вибірки, яка визначається відповідно до виду вибіркового обстеження; – довірче число або квантиль нормального розподілу (для =90% =1,65; для =95% =1,96; =99% =2,58).

2 Обчислення похибок репрезентативності

Формули обчислення середньої похибки для випадкової та систематичної вибірки*

Вид відбору	Формула розрахунку
для середнього	для сумарного	для частки
Безповторний
Повторний

* У цій та подальших таблицях наведені квадрати середніх похибок. Для того, щоб обчислення середньої похибки необхідно наведеного виразу дістати квадратний корінь.

Формули обчислення середньої похибки для стратифікованої вибірки*

Вид відбору	Розміщення одиниць вибірки за стратами	Формула розрахунку
для середнього	для сумарного	для частки
Безповторний	Пропорційне розміру страт
Пропорційне варіації ознаки в страті
Повторний	Пропорційне розміру страт
Пропорційне варіації ознаки в страті

 

Формули обчислення середньої похибки для кластерної вибірки*

Вид вибірки	Вид відбору	Формула розрахунку
для середнього	для сумарного	для частки
Кластерна	Безповторний
Повторний

3 Класи точності та надійності даних

Перед тим як поставити питання, які рівні точності і ймовірності варто вважати прийнятними, треба звернути увагу на те, що ці два параметри знаходяться у оберненій залежності один від одного. Сама ж відповідь не може бути однозначною, мова може йти лише про межі, в яких ці параметри повинні знаходитись.

Ні точність, ні ймовірність не є дискретними величинами, проте умовно їх можна шкалювати. Мають місце такі класифікації надійності (ймовірності) і точності (середньої похибки вибірки). Для класифікації надійності передбачається шість класів: практично достовірні дані (ймовірність вища 99,7%); з малим ризиком (95%); із середнім ризиком (80%); з підвищеним ризиком (60%); азартні (менше 60%), а також невизначені дані, коли ймовірність невідома.

Вибір класу надійності обумовлюється величиною можливих втрат від похибок розрахунку, можливістю компенсувати відхилення, факторами суб’єктивного порядку, зокрема ступенем відповідальності осіб, що прийматимуть рішення на основі даних вибіркового обстеження.

Що стосується граничної похибки, то практично виявляється достатньо високою точність на рівні 3%, а гранична відносна похибка вище 25% може бути для користувача непридатною (лише у окремих випадках з метою наближеної оцінки явища достатньо використовувати ще більш низьку точність).

Едельгауз поділив точність на п’ять класів. При цьому вибір потрібного класу ув’язувався з обсягом вибірки і з класами надійності. Так, при орієнтовних розрахунках (четвертий і п’ятий класи точності) не вимагалась 95% надійність. Але розрахунки по першому класу треба було орієнтувати на 99% надійність.