
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 6 Обчислення обсягу вибіркиСодержание книги
Поиск на нашем сайте
Перелік запитань
Методичні вказівки 1 Проблеми, що виникають при визначенні обсягу вибірки Одним з визначальних етапів планування вибіркового обстеження та формування вибірки є розрахунок обсягу вибіркової сукупності, необхідного для задоволення встановлених вимог. Від обсягу вибірки залежить якість результатів спостереження і вартість обстеження. Занадто великий обсяг вибірки призводить до невиправданих витрат та неефективного використання коштів, а недостатній обсяг вибірки – до незадовільної якості результатів обстеження. При визначенні обсягу вибірки існує складність: дисперсія ознаки в генеральній сукупності є невідомою. Тому використовуються наближені способи оцінки генеральної дисперсії, а саме: 1) дисперсія попередніх вибіркових обстежень, які проводились з аналогічною метою, за умови, що за час, який пройшов до нового обстеження, у генеральній сукупності не відбулось суттєвих змін; 2) дисперсія ознаки у генеральній чи вибірковій сукупності, аналогічній за своїми параметрами; 3) дисперсія у пробній вибірці, спеціально проведеній при визначенні шуканого розміру вибірки. Другою проблемою є визначення обсягу вибірки при різній дисперсії досліджуваних ознак. При проведенні вибіркових обстежень у анкету зазвичай включається не одна, а відразу велика кількість ознак. Це потрібно не тільки для економного використання ресурсів обстеження, але і для виявлення взаємозв’язків між ознаками. Проте кожна ознака має свою дисперсію і отже, для кожної ознаки потрібен власний обсяг вибірки. Ця обставина ускладнює ситуацію, тому що треба обрати один обсяг вибірки, що забезпечив би точність оцінок даного вибіркового обстеження. Цю складність можна подолати, якщо орієнтуватись на зведену ознаку, що потребує найбільшої чисельності вибірки. Тоді для інших зведених ознак ця чисельність буде напевне достатня. Проте при такій орієнтації на найгірші умови вибірки можливою є надлишковість інформації. У сукупності бувають такі ознаки, що мають значну варіацію і вимагають майже 100-відсоткової вибірки. У той час як для інших ознак необхідно забезпечити набагато менший обсяг вибірки. Рішення перше. У якості обсягу вибірки приймається кількість підприємств, що потрібна для ознаки, що потребує вибірку найбільшого обсягу. У цьому випадку підвищується ймовірність для інших ознак і є насправді надлишковою. Підвищений обсяг вибірки забезпечує обстеження усіх ознак у одному обстеженні. Рішення друге. Це рішення передбачає розрахунок за ознакою, для якої можна мати вибірку найменшого обсягу. Для інших ознак ймовірність буде занижена, на що повинна бути згода користувача. Рішення третє. Якщо зниження ймовірності в результаті другого рішення неприйнятне, то можна тією чи іншою мірою зниження рівня ймовірності компенсувати відповідним значенням рівня похибки – знову ж таки за згодою користувача. Рішення четверте. Замість одного вибіркового обстеження провести декілька. До такого рішення можна звернутись, якщо необхідно зберегти вихідні параметри по кожній з ознак, виходячи із замовлення користувача. Проте таке рішення веде до додаткових витрат. Крім цих рішень може виявитись доцільним і можливим: 1) враховувати важливість ознаки, знижуючи при цьому параметри менш важливих ознак; 2) організовувати для вивчення важливих для користувача ознак з високою дисперсією окремі обстеження з додатковим набором одиниць спостереження; 3) переглянути результати формування основи вибірки і шляхом стратифікації забезпечити більш однорідні групи одиниць обстеження; 4) в рамках організаційно єдиного вибіркового обстеження проводити декілька послідовних чи паралельних у часі вибіркових обстежень із різними (потрібними) обсягами вибіркової сукупності, об’єднавши при цьому в окремі групи ознаки з близькими параметрами, які потребують близьких за обсягом вибірок. Наступною важливою проблемою є те, що математичний апарат, який використовується для обчислення обсягу вибірки, вимагає наближення емпіричного розподілу сукупності до нормального. Проте в економічних дослідженнях фахівці мають справу переважно з розподілами, що характеризуються значною асиметрією, тобто досить сильно відрізняються від нормального розподілу. Розподіли, що відрізняються від нормального, дуже різноманітні як за своєю природою, так і за ступенем їхнього відхилення від нормального розподілу. Формула для обчислення обсягу вибірки із нормально розподіленої сукупності у випадку сильно анормального розподілу не буде точною. А отже, для таких розподілів апроксимація нормальним розподілом не може бути виправданою щодо кінцевого обсягу вибірки. Тому для кожного анормального розподілу потрібно використовувати власну формулу обсягу вибірки. 2 Вимоги до мінімального обсягу вибірки Обсяг вибірки повинен бути оптимальним. Із підвищенням обсягу вибірки підвищується точність та імовірність оцінки, але збільшуються витрати на проведення вибіркового обстеження. Із зниженням обсягу вибірки, навпаки, зменшуються витрати, але знижується точність та імовірність оцінки. Гранична похибка вибірки D – це критерій, що надає можливість знати, у яких межах досліджуваної ознаки може знаходитися невідома характеристика генеральної сукупності. Ця властивість граничної похибки дозволяє вважати її показником точності. Проте потрібно знати не тільки точність попадання, але і ступінь імовірності такого попадання. Коефіцієнт довіри ( Результати формування вибіркової сукупності, як відомо, у великій мірі залежать від прийнятих значень точності (граничної похибки вибірки) і ймовірності (коефіцієнта довіри). Прийняті до розрахунку показники точності і ймовірності встановлюються особою, що планує вибіркове обстеження, з урахуванням побажань користувачів. 3 Формули обчислення обсягу вибірки
|
||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 613; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.168.68 (0.006 с.) |

 або
або 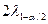 ) залежить від імовірності, із якою гарантується попадання оцінки характеристики в межі довірчого інтервалу.
) залежить від імовірності, із якою гарантується попадання оцінки характеристики в межі довірчого інтервалу.


