Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Показники для характеристики ряду динаміки, техніка їх обчислення й економічний змістСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Для відображення кількісних змін суспільних явищ у часі в статистиці застосовують такі показники: • рівень ряду динаміки; • абсолютний приріст; • коефіцієнт динаміки (зростання); • темп динаміки (зростання); • темп приросту; • абсолютне значення одного процента приросту; • середній темп динаміки та приросту; • середній абсолютний приріст; • коефіцієнт випередження; • процентні пункти зростання. Рівнем ряду динаміки називається первинне, абсолютне значення показника, що створює ряд динаміки. Розрізняють початковий рівень ряду, Y0,кінцевий Yп і середній Початковим рівнем називається перший член ряду динаміки (у табл. 4 — 20 тис. грн), а кінцевим — останній член (у табл. 4 — 64 тис. грн). Таблиця 4 Динаміка прибутку фірми за перше півріччя
Середній рівень періодичного (інтервального) ряду динаміки визначають за формулою простої середньої арифметичної в разі однакових проміжків часу між датами (повних рядів динаміки) і за формулою зваженої середньої арифметичної в разі різних проміжків часу (неповних рядів динаміки). На основі наведених у табл. 4 даних обчислимо середньомісячний прибуток фірми. Оскільки ряд динаміки періодичний, а часовий інтервал між датами однаковий (один місяць), застосуємо формулу простої середньої арифметичної:
Отже, у середньому фірма отримувала щомісячно 38 тис. грн прибутку. У разі різних проміжків часу між датами (неповного ряду динаміки) застосовують формулу зваженої середньої арифметичної, де як частоти беруть тривалість часового інтервалу між датами (табл. 5).
Таблиця 5 Динаміка середньомісячної заробітної плати в трудовому колективі
Середньомісячна заробітна плата становить
Середній рівень моментного ряду динаміки визначають за формулами простої середньої хронологічної (для повних рядів динаміки) і зваженої (для неповних). Таблиця 6 Динаміка чисельності докторів наук в Україні
Тепер за даними табл. 6 визначимо середню чисельність докторів наук за формулою середньої простої хронологічної:
Для ряду динаміки з різними проміжками часу застосовують формулу зваженої середньої арифметичної чи хронологічної. Визначимо середній офіційний курс гривні щодо долара США в березні 2003 р. (табл. 7). Таблиця 7 Офіційний курс гривні щодо долара США, установлений НБУ в березні 2003 р.
Отримаємо відповідно
Краще, якщо можливо, знайти суму варіант за всі дати періоду (15 днів) і розділити її на кількість дат у періоді. На жаль, така інформація не завжди є. Одне й те саме явище з часом змінює свої кількісні параметри: з віком змінюється вага дитини, її зріст; із плином часу змінюються кількісні параметри економічних явищ суспільства (ВВП, ціни, собівартість, продуктивність праці, рентабельність тощо). Завдання статистики — вивчити швидкість, інтенсивність цих змін, виявити тенденції та закономірності в їх розвитку. Цього можна досягти, порівнюючи рівні рядів динаміки. Коли в ряді динаміки три й більше рівнів, є два варіанти порівняння: базисний і ланцюговий. Можна порівнювати поточний, або звітний, рівень (Yп) із базисним (Y0) або попереднім (Yп-1), які називають базою порівняння. Якщо кожен рівень ряду динаміки (Yп) порівнюють із попереднім (Yп-1), то такі показники називають ланцюговими. Коли ж усі рівні (Yп) порівнюють з одним і тим самим рівнем — постійною базою порівняння (Y0), то такі показники називаються базисними (рис. 1).
Рис. 1. Принцип побудови базисних і ланцюгових показників динаміки Абсолютним приростом називається різниця між звітним і базисним рівнями. Він показує, як збільшився чи зменшився звітний рівень порівняно з базисним або попереднім періодом. Його визначають за формулами A=Yn – Y0, A=Yn – Yn-1 За даними табл. 8 обчислимо абсолютний приріст і занесемо результати до відповідних граф таблиці. Базисний абсолютний приріст порівняно з січнем становить у лютому 24 - 20 = 4 тис. грн, березні — 30 - 20 = 10 тис. грн, квітні — 36 - 20 = 16 тис. грн, травні — 64-20 = 34 тис. грн. Ланцюговий абсолютний приріст у лютому порівняно з січнем дорівнює 24 - 20 = 4 тис. грн, у березні порівняно з лютим — 30 - 24 = 6 тис. грн, у квітні порівняно з березнем — 36 -- 30 =6 тис. грн, у травні порівняно з квітнем — 54 - 36 = 18 тис. грн. Отже, між базисним і ланцюговим абсолютним приростом існує зв'язок: сума ланцюгових абсолютних приростів дорівнює останньому базисному. Абаз=∑Ал (у нашому прикладі — 4 + 6 + 6 + 18=34 тис. грн). Різниця між кожним наступним базисним абсолютним приростом і попереднім дорівнює відповідному ланцюговому приросту: 34 - 16 = 18; 16 - 10 = 6; 10 - 4 = 6 тис. грн. Коефіцієнт динаміки (зростання) обчислюють як відношення рівня досліджуваного періоду (Yп) до рівня, з яким порівнюють. Він показує, у скільки разів рівень звітного періоду збільшився порівняно з базисним або попереднім. Базисний і ланцюговий коефіцієнти динаміки визначають відповідно за формулами із точністю до третього десяткового знака (0,000).
Для даних табл. 8 базисні коефіцієнти динаміки в лютому, березні, квітні та травні дорівнюють 24/20 = 1,2; 30/20 = 1,5; 36/20 = 1,8; 54/20 = 2,7, а ланцюгові — відповідно 24/20 = 1,20; 30/24 = 1,25; 36/30 = = 1,20; 54/36 = 1,50. Отже, у травні порівняно з січнем прибуток фірми зріс у 2,7 раза, а порівняно з квітнем — в 1,5 раза. Між базисними і ланцюговими коефіцієнтами динаміки існує такий зв'язок: добуток ланцюгових показників динаміки дорівнює останньому базисному, а частка від ділення кожного наступного базисного на попередній дорівнює відповідному ланцюговому коефіцієнту (у нашому прикладі 1,20•1,25•1,20•1,50=2,7; 1,5/1,2 = 1,25; 1,8/1,5 = 1,20 і т. д.). Це дає змогу переходити від ланцюгових коефіцієнтів до базисних і навпаки, не маючи вихідних даних про обсяги прибутку фірми. Темп динаміки (зростання) обчислюють як процентне відношення рівня досліджуваного періоду (Yn) до рівня базисного чи попереднього. Він показує частку рівня звітного періоду до базисного чи попереднього, який беруть за 100%. Базисний і ланцюговий темпи зростання визначають відповідно за формулами
Очевидно, що ТД=КД∙100, а КД=ТД/100. Для даних таблиці 8 отримаємо такі значення цих показників: базисних— 1,2∙100=120; 1,5∙100=150; 1,8∙100=180; 2,7∙100=270; ланцюгових— 1,20∙100=120; 1,25∙100=125; 1,20∙100=120; 1,50∙100=150. Отже, у травні прибуток фірми становить 270 % до січня та 150 % до квітня, тобто він збільшився відповідно у 2,7 раза порівняно з січнем, і в 1,5 раза порівняно з квітнем.
Таблиця 8 Робоча таблиця для обчислення основних показників ряду динаміки
Темп приросту обчислюють діленням абсолютного приросту, помноженого на 100, на рівень, з яким порівнюють. Він показує, на скільки процентів рівень звітного періоду збільшився порівняно з базисним або попереднім. Базисний і ланцюговий темпи приросту визначають відповідно за формулами
а також віднявши 100 від значення темпів зростання: Тпр =ТД-100, Тпр=Кд∙100-100. Для даних табл. 8. базисні темпи приросту за лютий-травень становлять 120 - 100 = 20 %; 150 - 100 = 50 %; 180 - 100 = 80 %; 270-100=170%, а ланцюгові — 120-100=20 %; 125-100=25%; 120-100=20%; 150-100=50%. Отже, у травні порівняно з січнем прибуток фірми збільшився на 170 %, а порівняно з квітнем — на 50 %. Особливість темпів приросту полягає в тому, що з ними не можна виконувати ніяких арифметичних операцій. Типова задача 1. У січні ціни зросли на 8 %, у лютому — ще на 6 % і в березні — на 4 %. На скільки процентів ціни зросли за три місяці? Це ланцюгові темпи приросту, тому додавати їх не можна. Щоб розв'язати задачу, потрібно темпи приросту перетворити в ланцюгові коефіцієнти динаміки (зростання) та перемножити їх. Обчислення зручніше й наочніше виконувати за допомогою табл. 9. Таблиця 9 Динаміка цін на м'ясо на Центральному ринку
За період із січня до березня (за три місяці) ціни зросли на Т = (1,08 • 1,06 • 1,04) • 100-100 = 19,1 %. Типова задача 2. Порівняно з груднем минулого року в січні ціни зросли на 5 %, у лютому — на 8 %, у березні — на 12 % і у квітні — на 15 %. На скільки процентів зросли ціни в березні порівняно з лютим і у квітні порівняно з січнем? Обчислення краще подати в табл. 10. Таблиця 10 Динаміка цін на м'ясопродукцію
Щоб визначити, на скільки процентів ціни в березні зросли порівняно з лютим, потрібно базисний коефіцієнт динаміки березня поділити на базисний коефіцієнт динаміки лютого: 1,12 /1,08 = 1,037. Це ланцюговий коефіцієнт динаміки. Звідси Т = Кд • 100 - 100 = (1,037 • 100) - 100 ≈ 3,7 %, тобто ціни у березні зросли порівняно з лютим на 3,7 %. Щоб визначити, на скільки процентів зросли ціни у квітні порівняно з січнем, потрібно базисний коефіцієнт динаміки квітня розділити на базисний коефіцієнт динаміки січня. Отже ціни у квітні зросли порівняно з січнем в 1,15/1,05 = 1,095 раза, становлять 109,5 %, або зросли на 9,5 %. Абсолютне значення одного процента приросту обчислюють діленням абсолютного приросту на темп приросту. Воно показує, скільки припадає приросту в абсолютних величинах на кожен процент темпу приросту за відповідний період. Базисне та ланцюгове значення одного процента приросту визначають відповідно за формулами
Обчислимо цей показник за даними табл. 8. Його базисні значення в лютому-травні становлять 4/20 = 0,2; 10/50 = 0,2; 16/80 = 0,2; 34/170 = 0,2, а ланцюгові — відповідно 4/20 = 0,20; 6/25 = = 0,24; 6/20 = 0,30; 18/50 = 0,36 тис. грн. Абсолютне значення одного процента приросту, обчислене базисним способом, за кожний відрізок часу однакове й дорівнює 0,2 тис. грн, тобто Y0/100. На практиці А% обчислюють лише ланцюговим способом. Отже, у травні на кожний із 50 % приросту одержано 0,36 тис. грн приросту прибутку, тобто кожен процент приросту забезпечив фірмі додатково 360 грн. Спростимо наведені вище формули з урахуванням того, що
Отримаємо
Середній темп (коефіцієнт) динаміки (зростання) обчислюють за формулою середньої геометричної. Він показує, у скільки разів у середньому щомісячно протягом досліджуваного періоду зростав рівень базисного показника:
де Кд — середній коефіцієнт динаміки; К i — ланцюгові коефіцієнти динаміки; п — кількість ланцюгових коефіцієнтів. Якщо ланцюгові коефіцієнти невідомі, можна скористатися іншою формулою
де m — кількість рівнів ряду динаміки; Yп та Y0 — рівні відповідно звітного та базисного періодів. Обчислимо середній коефіцієнт динаміки (зростання) за період із січня до травня за даними табл. 8 за ланцюговими коефіцієнтами:
за базисними —
Одержаний коефіцієнт перетворюють у середній темп динаміки (зростання) за формулою
і середній темп приросту за формулами
Отже, за період із січня до травня прибуток щомісяця збільшувався в середньому в 1,282 раза, становив 128,2% (темп зростання), або збільшувався на 28,2 % (темп приросту). Обчислення проводять за допомогою логарифмів, або так званих таблиць Айрапетова. Середній абсолютний приріст обчислюють як просту середню арифметичну з ланцюгових абсолютних приростів:
де п — кількість ланцюгових приростів. Якщо ланцюгові прирости невідомі, середній абсолютний приріст можна визначити за формулою
де т — кількість календарних дат або рівнів ряду динаміки. Обчислимо цей показник зазначеними двома способами для даних табл. 8:
Отже, щомісячно за період із січня до травня (чотири місяці) прибуток фірми зростав у середньому на 8,5 тис. грн.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 552; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (0.011 с.) |

 .
.








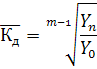
 ∙100
∙100
 - 100
- 100
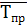


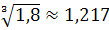
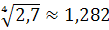
 ,
,