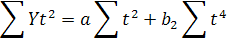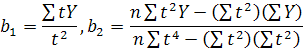Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поняття про ряди динаміки та їх видиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте ТЕМА 7. РЯДИ ДИНАМІКИ 1. Поняття про ряди динаміки та їх види 2. Показники для характеристики ряду динаміки, техніка їх обчислення й економічний зміст 3. Основні способи перетворення рядів динаміки Поняття про ряди динаміки та їх види Суспільні явища, які вивчає статистика, безперервно розвиваються, постійно змінюються в часі. У процесі історичного розвитку змінюється їх обсяг, рівень, склад, структура. Виявлення та вимірювання цих змін — одне з найважливіших завдань статистики. Для розв'язання таких завдань потрібно будувати динамічні ряди. Рядом динаміки в статистиці називається ряд чисел, що характеризує зміну суспільних явищ у часі (наприклад, динаміку роздрібного товарообороту, виробництва продукції промисловості, сільського господарства тощо). Важлива умова правильної побудови рядів динаміки — порівнянність їх показників. Для цього потрібно, щоб досліджувана сукупність протягом усього періоду дослідження стосувалася однієї й тієї самої території, одного й того самого кола об'єктів. Показники, якими характеризується сукупність, слід обчислювати за єдиною методикою, виражати в одних і тих самих одиницях виміру, порівнювати зазвичай за однакові проміжки часу. Кожний ряд динаміки складається з двох елементів: • статистичних показників, що характеризують розмір явища, тобто рівнів ряду; • ряду періодів, або моментів часу, яких стосуються рівні ряду (роки, квартали, місяці, декади, тижні, дні тощо). Таблиця 1 Динаміка чисельності населення, виробництва та споживання основних продуктів тваринництва в Україні
Наведемо класифікацію рядів динаміки: А. За формою подання розрізняють ряди динаміки абсолютних, відносних і середніх величин. Рядом динаміки абсолютних величин називається ряд, статистичні показники якого виражено абсолютними величинами: • динаміка загального обсягу товарообороту; • валового внутрішнього продукту; • чисельності населення тощо. Рядом динаміки відносних величин називають ряд, статистичні показники (ознаки) якого виражено відносними величинами, наприклад: • динаміка обсягу роздрібного товарообороту в процентах до 2000 р.; • частка державної торгівлі в загальному товарообороті; • зміна структури витрат виробництва й обігу за певні проміжки часу. Рядом динаміки середніх величин називається ряд, статистичні показники якого виражено середніми величинами, наприклад: • динаміка середньої заробітної плати чи середньої тривалості життя населення; • врожайність сільськогосподарських культур, продуктивність худоби, товарооборот на душу населення. Б. За часом реєстрації виокремлюють моментні ряди динаміки й інтервальні (періодичні). Моментним називається ряд динаміки, рівні якого характеризують стан явища на певний момент часу, наприклад: • чисельність населення, кількість банків, магазинів, митниць на певну дату; • обсяг товарних запасів, залишок грошей у касі на кінець робочого дня; • розмір статутного капіталу на початок місяця, активів і пасивів банку тощо. Показники (рівні) моментних рядів динаміки зазвичай не підсумовують, бо в кожному наступному показнику ряду міститься попередній або його частина. Водночас від кожного наступного рівня моментного ряду динаміки можна віднімати попередній, що дає можливість виявити, як змінився рівень ряду за досліджуваний період. Якщо в табл. 1 (графа Б) від чисельності населення 2001 р. (48,5 млн чол.) відняти чисельність населення у 2000 р. (49,7 млн чол.), то можна твердити, що за рік чисельність населення зменшилася на 1,2 млн чол. Періодичним (інтервальним) називається ряд динаміки, рівні якого характеризують розміри суспільних явищ за певні періоди (інтервали) часу, наприклад: • обсяг товарообороту продовольчих магазинів за рік; • виробництво продукції промисловості, сільського господарства; • споживання хліба за місяцями (сума дає споживання за рік). Рівні інтервального ряду динаміки можна підсумувати. На цьому ґрунтується застосування рядів нарощуваних підсумків. В. За часовим інтервалом між датами виділяють повні та неповні ряди. Повними називаються ряди динаміки з однаковими проміжками часу між датами (табл. 1), неповними — із різними (табл. 2). Таблиця 2 Кількість міських ринків в Україні
Г. За кількістю показників ряди динаміки поділяють на ізольовані та багатовимірні (комплексні). Ізольованими називаються ряди динаміки з одним показником (табл. 2), наприклад такі, у яких подано динаміку роздрібного товарообороту, заробітної плати чи забезпечення населення холодильниками. Багатомірними, або комплексними, називаються ряди динаміки, у яких прослідковується зміна двох і більше явищ, наприклад: динаміка споживання продуктів харчування на душу населення, забезпечення населення товарами тривалого користування, хворих на СНІД та ВІЛ-інфікованих.
Таблиця 3 Кількість ВІЛ-інфікованих і хворих на СНІД в Україні
Спостерігається чітко виражена тенденція до зростання кількості хворих на СНІД та ВІЛ-інфікованих.
Таблиця 8 Робоча таблиця для обчислення основних показників ряду динаміки
Темп приросту обчислюють діленням абсолютного приросту, помноженого на 100, на рівень, з яким порівнюють. Він показує, на скільки процентів рівень звітного періоду збільшився порівняно з базисним або попереднім. Базисний і ланцюговий темпи приросту визначають відповідно за формулами
а також віднявши 100 від значення темпів зростання: Тпр =ТД-100, Тпр=Кд∙100-100. Для даних табл. 8. базисні темпи приросту за лютий-травень становлять 120 - 100 = 20 %; 150 - 100 = 50 %; 180 - 100 = 80 %; 270-100=170%, а ланцюгові — 120-100=20 %; 125-100=25%; 120-100=20%; 150-100=50%. Отже, у травні порівняно з січнем прибуток фірми збільшився на 170 %, а порівняно з квітнем — на 50 %. Особливість темпів приросту полягає в тому, що з ними не можна виконувати ніяких арифметичних операцій. Типова задача 1. У січні ціни зросли на 8 %, у лютому — ще на 6 % і в березні — на 4 %. На скільки процентів ціни зросли за три місяці? Це ланцюгові темпи приросту, тому додавати їх не можна. Щоб розв'язати задачу, потрібно темпи приросту перетворити в ланцюгові коефіцієнти динаміки (зростання) та перемножити їх. Обчислення зручніше й наочніше виконувати за допомогою табл. 9. Таблиця 9 Динаміка цін на м'ясо на Центральному ринку
За період із січня до березня (за три місяці) ціни зросли на Т = (1,08 • 1,06 • 1,04) • 100-100 = 19,1 %. Типова задача 2. Порівняно з груднем минулого року в січні ціни зросли на 5 %, у лютому — на 8 %, у березні — на 12 % і у квітні — на 15 %. На скільки процентів зросли ціни в березні порівняно з лютим і у квітні порівняно з січнем? Обчислення краще подати в табл. 10. Таблиця 10 Динаміка цін на м'ясопродукцію
Щоб визначити, на скільки процентів ціни в березні зросли порівняно з лютим, потрібно базисний коефіцієнт динаміки березня поділити на базисний коефіцієнт динаміки лютого: 1,12 /1,08 = 1,037. Це ланцюговий коефіцієнт динаміки. Звідси Т = Кд • 100 - 100 = (1,037 • 100) - 100 ≈ 3,7 %, тобто ціни у березні зросли порівняно з лютим на 3,7 %. Щоб визначити, на скільки процентів зросли ціни у квітні порівняно з січнем, потрібно базисний коефіцієнт динаміки квітня розділити на базисний коефіцієнт динаміки січня. Отже ціни у квітні зросли порівняно з січнем в 1,15/1,05 = 1,095 раза, становлять 109,5 %, або зросли на 9,5 %. Абсолютне значення одного процента приросту обчислюють діленням абсолютного приросту на темп приросту. Воно показує, скільки припадає приросту в абсолютних величинах на кожен процент темпу приросту за відповідний період. Базисне та ланцюгове значення одного процента приросту визначають відповідно за формулами
Обчислимо цей показник за даними табл. 8. Його базисні значення в лютому-травні становлять 4/20 = 0,2; 10/50 = 0,2; 16/80 = 0,2; 34/170 = 0,2, а ланцюгові — відповідно 4/20 = 0,20; 6/25 = = 0,24; 6/20 = 0,30; 18/50 = 0,36 тис. грн. Абсолютне значення одного процента приросту, обчислене базисним способом, за кожний відрізок часу однакове й дорівнює 0,2 тис. грн, тобто Y0/100. На практиці А% обчислюють лише ланцюговим способом. Отже, у травні на кожний із 50 % приросту одержано 0,36 тис. грн приросту прибутку, тобто кожен процент приросту забезпечив фірмі додатково 360 грн. Спростимо наведені вище формули з урахуванням того, що
Отримаємо
Середній темп (коефіцієнт) динаміки (зростання) обчислюють за формулою середньої геометричної. Він показує, у скільки разів у середньому щомісячно протягом досліджуваного періоду зростав рівень базисного показника:
де Кд — середній коефіцієнт динаміки; К i — ланцюгові коефіцієнти динаміки; п — кількість ланцюгових коефіцієнтів. Якщо ланцюгові коефіцієнти невідомі, можна скористатися іншою формулою
де m — кількість рівнів ряду динаміки; Yп та Y0 — рівні відповідно звітного та базисного періодів. Обчислимо середній коефіцієнт динаміки (зростання) за період із січня до травня за даними табл. 8 за ланцюговими коефіцієнтами:
за базисними —
Одержаний коефіцієнт перетворюють у середній темп динаміки (зростання) за формулою
і середній темп приросту за формулами
Отже, за період із січня до травня прибуток щомісяця збільшувався в середньому в 1,282 раза, становив 128,2% (темп зростання), або збільшувався на 28,2 % (темп приросту). Обчислення проводять за допомогою логарифмів, або так званих таблиць Айрапетова. Середній абсолютний приріст обчислюють як просту середню арифметичну з ланцюгових абсолютних приростів:
де п — кількість ланцюгових приростів. Якщо ланцюгові прирости невідомі, середній абсолютний приріст можна визначити за формулою
де т — кількість календарних дат або рівнів ряду динаміки. Обчислимо цей показник зазначеними двома способами для даних табл. 8:
Отже, щомісячно за період із січня до травня (чотири місяці) прибуток фірми зростав у середньому на 8,5 тис. грн. Рис. 2. Сезонна хвиля Оскільки помісячні дані одного року часто випадкові, частіше користуються даними за кілька років (зазвичай за три). Тоді обчислюють помісячну середню за три роки, а з них — загальну середню. Індекс сезонності визначають як відношення помісячної середньої до загальної (табл. 17). Таблиця 17 Динаміка товарообороту овочевого магазину
Обчислимо помісячні статистичні середні: для січня — (44+44+41)/3 = 43, лютого — (45+ 43+ 43)/3 = 44 і т. д. Потім визначимо середньомісячну середню за три роки:
Нарешті, обчислимо індекси сезонності як відношення помісячних середніх до середньомісячної за три роки: для січня — (43/57)·100=75%; лютого— (44/57)·100 = 77% і т. д. Обчислені індекси сезонності характеризують сезонну хвилю реалізації овочевої продукції та розмах її коливання за місяцями року. Є й інші способи вимірювання сезонності: метод помісячних відношень, гармонічний аналіз тощо. Інтерполяція й екстраполяція. Інтерполяція — це визначення невідомого рівня всередині ряду динаміки. Це можна зробити за допомогою таких показників: • середньої арифметичної суміжних із невідомим рівнів; • середніх абсолютних приростів із суміжних рівнів; • середніх темпів зростання із суміжних рівнів. Типова задача 1. Зростання заробітної плати характеризується такими даними:
Потрібно віднайти заробітну плату за березень. 1. Використаємо середню арифметичну рівнів, суміжних із невідомим:
Отже, у березні заробітна плата становила 335 грн. 2. Визначимо середній абсолютний приріст із суміжних:
Тоді заробітна плата в березні дорівнює сумі заробітної плати в лютому та середнього приросту (330 + 5 = 335 грн), або різниці заробітної плати у квітні та приросту (340 - 5 = 335 грн). 3. Обчислимо середній темп зростання із суміжних:
Щоб визначити березневу заробітну плату, потрібно заробітну плату лютого помножити на знайдений коефіцієнт (330 • 1,015 ≈ 335 грн) або поділити на нього заробітну плату квітня (340/1,015 ≈ 335 грн). Екстраполяція — це визначення невідомого рівня за межами ряду динаміки. Розрізняють перспективну та ретроспективну екстраполяцію. Перспективна екстраполяція — це визначення невідомих рівнів ряду динаміки в майбутньому періоді на основі виявленої закономірності зміни досліджуваного явища у відомому періоді. Цей метод широко застосовується у плануванні та прогнозуванні розвитку економічних явищ і процесів. Ретроспективна екстраполяція — це визначення невідомих рівнів ряду динаміки в минулому. Це можна зробити за допомогою таких показників: • середнього абсолютного приросту
• середніх темпів зростання
Типова задача 2. За нижченаведеними даними визначити перспективну чисельність населення у 2000, 2001 та 2005 р. Таблиця 18 Робоча таблиця для екстраполяції чисельності населення України
Обчислимо середній абсолютний приріст за формулою
де Yn — чисельність населення у звітному періоді (1999 р.); Y0 — чисельність населення в базовому періоді (1995 р.); т — кількість календарних дат (1995-1999 рр.), або рівнів ряду динаміки.
Тоді Y1996=51,700 + (-0,375)·1 = 51,325 млн чол., Y1997 =51,700 +(-0,375)·2=50,950 млн чол., Y2000 =51,700+(-0,375)·5 = 49,825 млн чол., Y2001 =51,700 + (-0,375)·6 = 49,450млнчол., Y2005=51,700 + (-0,375) ·10= =47,950 млн. чол. Фактична ж чисельність населення за даними Держкомстату України становила в 2000 р. 49,7 млн чол., а у 2001 р. — 49,3 млн чол., в 2005 — 47,6 млн чол. Похибка становить менше одного проценту. Тепер розв'яжемо задачу другим способом. Спочатку обчислимо середній темп динаміки за формулою
де Yn, Y0 — чисельність населення відповідно у звітному та базисному періодах; т — кількість календарних років у періоді або рівнів ряду динаміки. Тут т = 5, тому
Тоді Щоб успішно застосовувати методи екстраполяції й інтерполяції, потрібно досконало знати закони розвитку досліджуваних явищ і процесів. Без цього прогнози та плани, складені за принципом "від досягненого", будуть нереальними. Аналітичне вирівнювання. Цей метод полягає у визначенні розрахункових (теоретичних, вирівняних) значень рівнів ряду динаміки та заміні ними фактичних, щоб виявити закономірності розвитку явища (процесу). Його застосовують зазвичай тоді, коли безпосередньо з показників ряду динаміки не вдається виявити чіткої закономірності, тенденції розвитку. У більшості розрахунків застосовують переважно метод найменших квадратів. Він полягає в тому, що потрібно знайти таку пряму на графіку, ординати точок якої найближчі до значень фактичного динамічного ряду. Рівняння прямої можна записати у вигляді
де Потрібно розв'язати це рівняння щодо a й b. Для цього складають і розв'язують так звані нормальні рівняння, одержані способом найменших квадратів:
де п — кількість років у аналізованому періоді. Цю систему рівнянь можна спростити, якщо починати відлік часу із середини ряду, умовно взятого за нуль. Тому в кожному конкретному випадку Σt = 0. Тоді система рівнянь набере вигляду
звідки
Продемонструємо методику розрахунку на такому прикладі (табл. 19). Таблиця 19 Робоча таблиця для аналітичного вирівнювання ряду динаміки вздовж прямої (на прикладі врожайності картоплі в Україні)
Підставивши значення а й b у формулу
обчислимо теоретичне значення для кожного року. Отримаємо вирівняний ряд, без випадкових коливань із незначним збільшенням. Згідно з ним урожайність картоплі в Україні з 1995 до 2001 р. має тенденцію до незначного зростання, хоча з офіційних даних для цього періоду такої тенденції не видно. Є й інші способи вирівнювання, які вивчають економетрія, теорія ймовірностей і математична статистика. Застосування в статистиці методів збільшення інтервалів і плинної середньої дає змогу виділити тренд, але одержати узагальнювальну його оцінку за допомогою цих методів неможливо. Для цього в статистиці застосовують метод аналітичного вирівнювання, за допомогою якого не тільки виявляють тенденцію розвитку явищ і процесів, але й кількісно вимірюють їх. Тенденцію ряду описують функцією від часу f(t), лінійною чи криволінійною. Вирівнювання зводиться до вибору функції, ординати точок якої максимально наближені до емпіричних значень динамічного ряду. Найпоширеніші такі функції: • пряма Yt = а+bt; • гіпербола Yt=а+b/t; • показникова Yt = abt • парабола другого порядку Yt=a+b1t+b2t2; • парабола третього порядкуYt=a+b1t+b2t2+b3t3; • рядФур'є Вибір функції аналітичного вирівнювання рядів динаміки грунтується на теоретичному аналізі сутності досліджуваних явищ і процесів у сфері соціальної чи економічної діяльності. У разі більш-менш постійних абсолютних приростів, коли рівні динамічного ряду змінюються в арифметичній прогресії, вирівнювання виконують за допомогою прямої Yt=a+bt де Y — вирівняне значення динамічного ряду; а, b — параметри прямої (початковий і щорічний прирости); t — порядковий номер періоду (умовне позначення часу). Параметри а, b визначають за допомогою методу найменших квадратів, розв'язуючи систему нормальних рівнянь
де Y — фактичний рівень ряду динаміки; п — кількість членів ряду динаміки. Для зручності розрахунків відлік часу доцільно робити із середини ряду так, щоб сума часу дорівнювала нулю: Σt = 0. Якщо кількість рівнів непарна, серединний момент позначають нулем, попередні періоди — від'ємними числами, наступні — додатними:
Якщо кількість рівнів динамічного ряду парна, то два серединні моменти часу позначають числами -1 і 1, а інші— через два інтервали: попередні — від'ємними, наступні — додатними числами:
Якщо Σ t = 0, система рівнянь для обчислення значень а й b має такий вигляд:
Розв'язавши її, одержимо:
Ще раз розглянемо методику вирівнювання динаміки доходу банку за рівнянням прямої на умовному прикладі (табл. 20). Для розрахункових даних таблиці обчислимо параметри а й b:
Таблиця 20 Схема аналітичного вирівнювання ряду динаміки доходу банку рівнянням прямої
Тоді рівняння тренду має вигляд Yt=322,8+13,54t Із нього випливає, що в середньому дохід банку зростав щороку приблизно на 14 млн грн. Послідовно підставляючи в це рівняння значення t, отримаємо вирівняний ряд динаміки доходу банку, абстрагований від випадкових коливань, який зростає (остання графа табл. 20). Можна перевірити правильність розрахунку, порівнявши ΣY та ΣYt,. Для даних із табл.20 Σ Y = 4842 = Σ Yt, тобто рівні вирівняного ряду обчислено правильно. Вирівнювання гіперболою. Його виконують тоді, коли з плином часу динаміка діяльності спадає чи зростає до певної межі. Способом найменших квадратів обчислимо значення параметрів а та А для рівняння гіперболи
Для цього скористаємося системою нормальних рівнянь
Оскільки в разі згладжування гіперболою значення t неможливо вибрати симетрично щодо 0, то умова Σ t = 0 не виконується. У зв'язку з цим система нормальних рівнянь не спрощується. Виконаємо вирівнювання вздовж гіперболи на умовному прикладі, який відбиває динаміку обсягу витрат обігу супермаркету (табл. 21). Таблиця 21 Схема аналітичного вирівнювання ряду динаміки витрат обігу рівнянням гіперболи
293=6a+2,45b 148=2,45a+1,49b Розв'язавши систему, отримаємо а ≈ 25,10; b = 58,13. Тоді рівняння гіперболи має вигляд В останній графі табл. 21 наведено теоретичні значення Yt Вирівнювання параболою другого порядку. У разі вирівнюванні параболою другого порядку Yt = a+b1t+b2t2 параметри а, b1, b2 також визначимо методом найменших квадратів. Для цього розв'яжемо систему нормальних рівнянь
Вона має такий розв'язок:
Розглянемо на прикладі вирівнювання динамічного ряду кількості клієнтів банку рівнянням параболи другого порядку. Для цього побудуємо розрахункову табл. 22. Таблиця 22 Схема аналітичного вирівнювання ряду динаміки кількості клієнтів банку рівнянням параболи другого порядку
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 484; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.015 с.) |

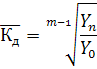
 ∙100
∙100
 - 100
- 100
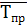


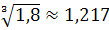
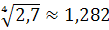
 ,
,


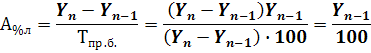











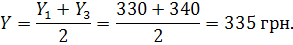







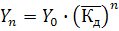 , Y2000 =51,700·0,99275=49,840 млн. чол., Y2001 =51,700·0,99276 = 49,476 млн. чол., Y2005 =51,700·0,992710=48,047млн. чол.
, Y2000 =51,700·0,99275=49,840 млн. чол., Y2001 =51,700·0,99276 = 49,476 млн. чол., Y2005 =51,700·0,992710=48,047млн. чол.



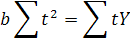
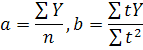
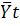

 ,
,
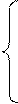



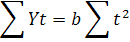

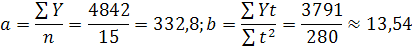
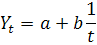
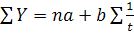
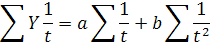

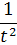

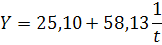
 Визначимо параметри а та b, підставивши в систему рівняння параметри, обчислені в табл. 21:
Визначимо параметри а та b, підставивши в систему рівняння параметри, обчислені в табл. 21: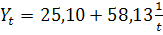 .
.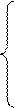
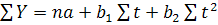
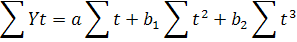

 Якщо Σ t =0, то Σ t 3 =0. Тоді система рівнянь має вигляд
Якщо Σ t =0, то Σ t 3 =0. Тоді система рівнянь має вигляд