
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Агрегатна форма загальних індексів якісних і змішаних показниківСодержание книги
Поиск на нашем сайте
Загальні індекси агрегатної форми якісних показників (цін, собівартості, продуктивності праці тощо) будуються за тією ж методологією, що і агрегатні індекси кількісних показників. Для приведення якісних показників до порівняльного виду утворюються агрегати в чисельнику і знаменнику індексів у вигляді добутку індексованих величин на відповідні постійні ваги кількісних показників. В більшості випадків ваги фіксуються на рівні поточного (звітного) періоду або (в меншій мірі) - на рівні базисного періоду. Серед агрегатних індексів якісних показників значна роль відводиться агрегатному індексу цін Ір, який в більшості випадків використовується у двох формах: індексу Пааше та індексу Ласпейреса. Індекс цін Пааше запропоновано в 1874 р. німецьким економістом Г. Пааше. В індексі у якості ваги використовується обсяг продукції певного виду в поточному періоді <?;. Індекс Пааше розраховується за формулою:
де р1, р0 - індексовані величини цін на певний вид продукції відповідно у поточному та базисному періодах; Індекс цін Пааше характеризує вплив зміни цін на вартість кількості товарів, які реалізовані в поточному періоді. Розрахований за формулою агрегатний індекс цін Пааше показує, в скільки разів збільшився (зменшився) у середньому рівень цін на масу товару, що реалізовано в поточному періоді, або скільки процентів складає його зріст (зменшення) в поточному періоді у зрівнянні з базисним періодом. Наприклад, якщо Ір=0,98, або 98%, то це означає, що рівень цін на товари, які реалізовано в поточному періоді, в середньому зменшився в 0,98 рази, або на 2% (100-98=2%) у зрівнянні з базисним періодом. В разі Ір>1,0 (або 100%) говорять про збільшення рівня цін в поточному періоді порівняно з базисним періодом. Різниця чисельника і знаменника Проте слід зазначити, що вибір ваг при побудові агрегатного індексу цін не можна рахувати обов 'язковим у всіх випадках. В статистиці ряд задач можуть і повинні вирішуватись по різному в залежності від конкретної мети та особливостей дослідження. Проілюструємо це таким прикладом. Відомо, що в період економічної кризи різко зростають ціни. В результаті ряд продуктів випадають із споживання населення, особливо малозабезпечених. Припустимо, що в умовному базисному періоді у склад споживання входило 30 найменувань продуктів (q0=30), а в поточному періоді - тільки 25 найменувань (q1=25). Очевидно, що в такій ситуації індекс цін, розрахований за q1, невірно відобразить зміну цін на ті продукти, які випали із споживання при надмірному зростанні цін. Тому в подібних випадках більш правильно відобразить зміну цін індекс, побудований за продукцією базисного періоду. В 1864 р. німецьким економістом Е. Ласпейресом запропоновано індекс Ласпейреса, де в якості ваги використовується обсяг продукції за різновидністю товарів у базисному періоді ц0. Індекс Ласпейреса розраховується за формулою:
де
Індекс Ласпейреса показує вплив зміни цін на вартість кількості товарів, які реалізовано в базисному періоді. Таким чином, індекси цін Пааше і Ласпейреса не ідентичні і для однакових вихідних даних не співпадають, так як мають різний економічний зміст: індекс Ласпейреса використовують у прогнозуванні обсягу товарообороту у зв'язку з ймовірною зміною цін на товари в майбутньому періоді, індекс Пааше використовують при вивченні звітних даних, коли ціллю аналізу є якісна оцінка зміни товарообороту в результаті зміни цін у звітному періоді. Індекс Ласпейреса (L) в ряді випадків більше індексу Пааше (Р). Ця систематична залежність двох індексів відома в статистиці як ефект Гершенкрона. Враховуючи наявну розбіжність між індексами Пааше і Ласпейреса, І. Фішером у міжнародному зіставленні запропоновано "ідеальний індекс" (індекс Фішера), як середньогеометрич-на величина з двох вищезгаданих індексів:
Але цей індекс не получив широкого розповсюдження в статистичній практиці країн світу через відсутність в індексі конкретного економічного змісту. На теперішній час лишається проблема вибору універсальної системи зважування в агрегатних індексах цін. Проте вона компромісно вирішується використанням індексів Пааше чи Ласпейреса в конкретних умовах застосування. В економічному аналізі явищ і процесів використовуються і інші агрегатні індекси якісних показників: собівартості продукції Iz, продуктивність праці It, та ін. Агрегатний індекс собівартості продукції розраховується за формулою:
де z1, z0 - собівартість одиниці продукції певного виду відповідно у поточному та базисному періодах (індексуємі величини); q1 — кількість виробленої продукції кожного виду у поточному періоді, яка приймається в якості ваги; Розрахований за формулою індекс собівартості показує, в скільки разів зменшився (зріс) у середньому рівень собівартості на продукцію, вироблену у поточному періоді, або скільки процентів складає його зменшення (зріст) в поточному періоді у зрівнянні з базисним. Якщо із значення індексу собівартості у процентах відрахувати 100%, то різниця (Iz-100) покаже, на скільки процентів у середньому зменшився (збільшився) рівень собівартості на продукцію, вироблену у поточному періоді. Різниця між чисельником і знаменником індексу Продуктивність праці - це результат конкретної живої праці, ефективність цілеспрямованої діяльності людей у виготовленні продукції на протязі відповідного проміжку часу. Виміряється кількістю споживчих вартостей, вироблених в одиницю часу, або кількістю часу, витраченого на одиницю продукції. Продуктивність праці важлива для успішного рішення багатьох соціальних і економічних задач. Тільки в наслідок неухильного зростання продуктивності праці можна забезпечити динамічний продуктивний розвиток виробництва, повисити рівень життя населення. Агрегатний індекс продуктивності праці за витратами праці на одиницю продукції розраховується за формулою:
де t0, t1 - затрати робочого часу на одиницю продукції (трудомісткість) відповідно у базисному і поточному періодах; q1 - обсяг продукції поточного періоду; На відміну від наведених вище формул інших агрегатних індексів, в цьому індексі базисна величина індексуємого показника (tо) знаходиться в чисельнику, а поточна величина (t1) - в знаменнику. Це відбувається тому, що затрати праці на одиницю продукції і продуктивність праці зв'язані оберненою залежністю. Розрахований за формулою індекс продуктивності праці показує, у скільки разів зріс (зменшився) в середньому загальний рівень трудомісткості поточного (звітного) періоду у зрівнянні з базисним. Якщо із значення індексу продуктивності праці в процентах відрахувати 100%, то різниця (It,-100) покаже, на скільки процентів в середньому зріс (зменшився) на цей час рівень трудомісткості. Різниця чисельника і знаменника індексу Агрегатні індекси якісних показників можуть розраховуватись у вигляді індексного ряду. При цьому, як у наведеному прикладі для агрегатного індексу фізичного обсягу продукції, використовуються ланцюговий та базисний спосіб розрахунку для індексів з постійними та змінними вагами. До основних агрегатних індексів змішаних показників можна віднести індекси вартості (товарообороту) товарів Іpq, індекси загальної собівартості продукції Іzq, індекси загальних витрат робочого часу Itq тощо. Такі індекси можна подати у вигляді добутку двох індексів, або системою індексів, що зручно для аналізу складного явища під впливом певних факторів. Так як агрегатний індекс вартості товарів (товарообороту) можна представити як добуток індексу цін Ір (у формі індексу Пааше) та індексу фізичного обсягу продукції Іq Ipq=Ip*Iq Як видно із виразу, цей індекс являє собою відношення вартості товарів поточного (звітного) періоду до вартості товарів базисного періоду. Індекс показує, в скільки разів зросла (зменшилась) вартість товарів (товарооборот) поточного періоду у зрівнянні з базисним, або скільки процентів складає зростання (зменшення) вартості товарів. Якщо із індексу вартості, вираженому в процентах, відняти 100%, то різниця (Іpq - 100) показує на скільки процентів змінилась вартість товарів в поточному періоді у зрівнянні з базисним. Різниця чисельника і знаменника формули
показує, на скільки грошових одиниць змінилась вартість товарів у поточному періоді у зрівнянні з базисним. Якщо відомі два з індексів, то на підставі цієї залежності можна знайти третій індекс. Аналогічно агрегатний індекс загальної собівартості продукції Іqz можна представити як добуток індексу собівартості Iz та індексу фізичного обсягу продукції за собівартістю Іq у вигляді Izq=Iz*Iq Або який показує зіставлення витрат на виробництво продукції у поточному і базисному періодах і виражається у коефіцієнтах або процентах. Агрегатний індекс загальних витрат робочого часу Іtq представляється у вигляді добутку індексу продуктивності праці It, та індексу фізичного обсягу продукції за продуктивністю праці Iq Itq=It*Iq або Його величина дає порівняння витрат робочого часу на виробництво продукції різних видів у поточному і базисному періодах. Індекс валового збору врожаю Іys можна подати як добуток індексу Іу та структури посівних площ Іs Iys=Iy*Is Або Середньозважені індекси Агрегатний спосіб представлення загальних індексів в статистиці є найбільш розповсюдженим. Разом з тим використовується і інший спосіб розрахунку загальних індексів як середніх із відповідних індивідуальних індексів, або середньозважених індексів. До розрахунку середньозважених індексів звертаються у тих випадках, коли первинна (вихідна) інформація не дозволяє розрахувати загальний агрегатний індекс. Існують дві форми середньозважених індексів: середньоарифметична та середньо-гармонічна. Як правило, середній арифметичний індекс застосовується при індексуванні кількісних показників (наприклад, фізичного обсягу продукції), а середній гармонічний - при індексуванні якісних показників (наприклад, цін). До розрахунку середнього арифметичного індексу вдаються тоді, коли індексована величина чисельника виражається через індивідуальний індекс. Наприклад, необхідно обчислити загальний індекс фізичного обсягу продукції Іq коли з вихідних даних відомі індивідуальні індекси фізичного обсягу (Iq=qq/q0) і вартість продукції кожного виду за базисний період (q0р0). Тоді загальний індекс фізичного обсягу можна визначити як середню арифметичну зважену із індивідуальних індексів. Для цього змінимо невідому кількість продукції звітного періоду (q1) добутком iqq0 в чисельнику агрегатного індексу. Тоді загальний індекс фізичного обсягу продукції набуде вигляду: Ця формула являє собою середню арифметичну з індивідуальних індексів фізичного обсягу продукції, зважену за вартістю продукції базисного періоду. Якщо індексована величина виражається через індивідуальний індекс у знаменнику, то індекс має назву середнього гармонічного індексу. Наприклад, відомі індивідуальні індекси цін ( Внаслідок цього знаменник агрегатної форми індексу цін набуде вигляду
Ця формула представляє собою середню гармонічну з індивідуальних індексів цін, зважену за обсягом продукції поточного періоду.
|
|||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 532; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.192.64 (0.008 с.) |


 - вартість всієї продукції у поточному періоді;
- вартість всієї продукції у поточному періоді;  - умовна вартість продукції поточного періоду за порівнюваними цінами базисного періоду.
- умовна вартість продукції поточного періоду за порівнюваними цінами базисного періоду. свідчить про абсолютну економію (-) (Δр<0) або абсолютну перевитрату (+) (Δр>0) грошових коштів покупців в результаті зміни цін на ці товари.
свідчить про абсолютну економію (-) (Δр<0) або абсолютну перевитрату (+) (Δр>0) грошових коштів покупців в результаті зміни цін на ці товари.
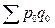 - вартість продукції у базисному періоді.
- вартість продукції у базисному періоді.

 - витрати на виробництво продукції поточного періоду;
- витрати на виробництво продукції поточного періоду;  - умовні витрати на виробництво тієї ж продукції, якщо б собівартість одиниці продукції була на рівні базисного періоду.
- умовні витрати на виробництво тієї ж продукції, якщо б собівартість одиниці продукції була на рівні базисного періоду. характеризує економію (-) або перевитрати (+) від зміни собівартості одиниці продукції.
характеризує економію (-) або перевитрати (+) від зміни собівартості одиниці продукції.
 - умовні затрати робочого часу(трудомісткість) на всю продукцію базисного періоду;
- умовні затрати робочого часу(трудомісткість) на всю продукцію базисного періоду;  - фактичні затрати робочого часу на всю продукцію поточного періоду.
- фактичні затрати робочого часу на всю продукцію поточного періоду. показує зростання (Δt >0) або зменшення (Δt<0) трудомісткості на всю продукцію базисного періоду у зрівнянні з поточним.
показує зростання (Δt >0) або зменшення (Δt<0) трудомісткості на всю продукцію базисного періоду у зрівнянні з поточним.





 ) і вартість кожного виду продукції за поточний (звітний) період (q1p1), але невідомі дані про ціну за одиницю продукції за базисний період (ро). Щоб знайти середній гармонічний індекс цін, у знаменнику агрегатного індексу ціну базисного періоду (р0) запишемо рівним ш відношенням
) і вартість кожного виду продукції за поточний (звітний) період (q1p1), але невідомі дані про ціну за одиницю продукції за базисний період (ро). Щоб знайти середній гармонічний індекс цін, у знаменнику агрегатного індексу ціну базисного періоду (р0) запишемо рівним ш відношенням 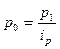
 , а індекс цін матиме вигляд:
, а індекс цін матиме вигляд:



