
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Погрешности косвенных измеренийСодержание книги
Поиск на нашем сайте
Задача ставится так: пусть искомая величина z определяется через другие величины a, b, c,..., полученные при прямых измерениях z = f (a, b, c,...) (1.11) Необходимо найти среднее значение функции и погрешность ее измерений, т.е. найти доверительный интервал
при надежности a и относительную погрешность Что касается
Абсолютная погрешность косвенных измерений
Здесь Если величины a, b, c,... в функцию Z = f (a, b, c,...) входят в виде сомножителей в той или иной степени, т. е. если
то сначала удобно вычислить относительную погрешность
а затем абсолютную
Формулы для D z и ez часто приводятся в справочной литературе. Примечания. 1. При косвенных измерениях в расчетные формулы могут входить известные физические константы (ускорение свободного падения g, скорость света в вакууме с и т. д.), числа типа Принято считать, что погрешность округления приближенного числа равна половине единицы того разряда, до которого это число было округлено. Например,p = 3,14159.... Если взять p= 3,1, то Dp = 0,05, если p = 3,14, то Dp = 0,005... и т.д. Вопрос о том, до какого разряда округлять приближенное число, решается так: относительная ошибка, вносимая округлением, должна быть того же порядка или на порядок меньше, что и максимальная из относительных ошибок других видов. Таким же образом оценивается абсолютная ошибка табличных данных. Например, в таблице указано r =13,6×103 кг/ м3, следовательно,Dr = 0,05×103 кг/м3. Ошибка значений универсальных постоянных часто указывается вместе с их принятыми за средние значения: (с = 2. Иногда при косвенных измерениях условия опыта при повторных наблюдениях не совпадают. В этом случае значение функции z вычисляется для каждого отдельного измерения, а доверительный интервал вычисляется через значения z так же, как при прямых измерениях (все погрешности здесь входят в одну случайную погрешность измерения z). Величины, которые не измеряются, а задаются (если они есть) должны быть указаны при этом с достаточно большой точностью. В качестве итога всего, сказанного выше, приведем порядок обработки результатов измерений.
Порядок обработки результатов измерений Прямые измерения 1. Вычислить среднее значение для n измерений
2. Найти погрешности отдельных измерений 3. Вычислить квадраты погрешностей отдельных измерений и их сумму: 4. Задать надежностьa (для наших целей принимаем a= 0,95) и по таблице определить коэффициенты Стьюдента t a,nи ta,¥. 5. Произвести оценку систематических погрешностей: приборной D хпр и ошибки округления при измеренияхD х окр= D/2 (D - цена деления прибора) и найти полную погрешность результата измерений (полуширину доверительного интервала):
6. Оценить относительную погрешность
7. Окончательный результат записать в виде
Косвенные измерения
1. Для каждой величины, измеренной прямым способом, входящей в формулу для определения искомой величины 2. Определить среднее значение искомой величины z = f (<a>,<b>,<c>,...).
3. Оценить полуширину доверительного интервала для результата косвенных измерений
где производные 4. Определить относительную погрешность результата
5. Если зависимость z от a, b, c,... имеет вид
а затем абсолютную 6. Окончательный результат записать в виде z = <z> ± Dz...% при a =. Примечание: При обработке результатов прямых измерений нужно следовать следующему правилу: численные значения всех рассчитываемых величин должны содержать на один разряд больше, чем исходные (определенные экспериментально) величины. При косвенных измерениях вычисления В окончательной записи абсолютной погрешности следует оставлять только одну значащую цифру. (Если этой цифрой окажется 1 или 2, то после нее сохраняют еще одну цифру). Среднее значение округляется до того же результата, что и абсолютная погрешность. Например: V = I = Порядок выполнения работы Определение диаметра цилиндра. 1. Микрометром или штангенциркулем измерить не менее 7 раз (в разных местах и направлениях) диаметр цилиндра. Результаты записать в таблицу. 2. Вычислить среднее значение диаметра <d> = где n - число измерений, i - номер измерения. 3. Вычислить D di = (di - <d>), D di2 и
4. Задавшись надежностью a (от 0,90 до 0,97), по таблице выбрать коэффициенты Стьюдента t a,n и t a,¥. 5. Определить приборную погрешность D d пр. Для микрометраD d пр = D/2 (D - цена деления микрометра, равная обычно 0,01 мм). Для штангенциркуля D d пр = D, D - “цена” деления нониуса. 6. Вычислить абсолютную ошибку (полуширину доверительного интервала) в определении диаметра цилиндра:
7. Вычислить относительную погрешность e d = D d/<d>.
Определение высоты цилиндра Все измерения и вычисления, выполненные при определении диаметра цилиндра, повторить при той же надежностиa для высоты цилиндра h. Результаты записать в таблицу.
Определение объема цилиндра 1. Вычислить среднее значение объема цилиндра <V> = p/4 <d>2 <h>. 2. Вычислить относительную погрешность определения объема
3. Вычислить полуширину доверительного интервала D V = ev <V>. 4. Результаты записать в виде V =<V> ± D V приa =... ev =...%,.
ЛАБОРАТОРНАЯ РАБОТА № 2 МАЯТНИК ОБЕРБЕКА
Цель: познакомиться с динамическими характеристиками вращательного движения твердого тела, а также с использованием основного закона динамики вращательного движения. Приборы и принадлежности: маятник Обербека, секундомер, мерительная линейка, штангенциркуль.
|
|||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 299; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.42.34 (0.005 с.) |

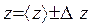 (1.12)
(1.12)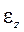
 .
. , то оно находится путем подстановки в правую часть (11) вместо a, b, c,... их средних значений
, то оно находится путем подстановки в правую часть (11) вместо a, b, c,... их средних значений . (1.13)
. (1.13) является функцией абсолютных погрешностей прямых измерений и вычисляется по формуле
является функцией абсолютных погрешностей прямых измерений и вычисляется по формуле (1.14)
(1.14) частные производные функции f по переменным a, b,..
частные производные функции f по переменным a, b,..
 , (1.15)
, (1.15)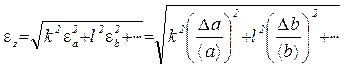 , (1.16)
, (1.16)
 (1.17)
(1.17)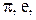 дробные множители
дробные множители  .... Эти величины при вычислениях округляются. При этом, естественно, в расчет вносится погрешность
.... Эти величины при вычислениях округляются. При этом, естественно, в расчет вносится погрешность  - погрешность округления при вычислениях, которая должна учитываться.
- погрешность округления при вычислениях, которая должна учитываться. м/c, где D с = 0,3×103 м/c.
м/c, где D с = 0,3×103 м/c. .
. .
. .
. .
. 100 %.
100 %. % при a =...
% при a =... , провести обработку, как указано выше. Если среди величин a, b, c,... есть табличные константы или числа типа p, е,..., то при вычислениях
, провести обработку, как указано выше. Если среди величин a, b, c,... есть табличные константы или числа типа p, е,..., то при вычислениях  округлять их следует так (если это возможно), чтобы вносимая при этом относительная ошибка была на порядок меньше наибольшей относительной ошибки величин, измеренных прямым способом.
округлять их следует так (если это возможно), чтобы вносимая при этом относительная ошибка была на порядок меньше наибольшей относительной ошибки величин, измеренных прямым способом. ,
, .......вычисляются при
.......вычисляются при 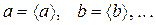
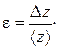 100 %.
100 %. , где k, l, m - любые действительные числа, то сначала следует найти относительную ошибку
, где k, l, m - любые действительные числа, то сначала следует найти относительную ошибку ,
, .
. производить по правилам приближенных вычислений.
производить по правилам приближенных вычислений.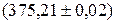 см
см  =
=  см
см  A =
A =  Дж.
Дж.
 .
.
 .
. где ep = Dp/p.
где ep = Dp/p. Сумма
Сумма



