
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение цены деления окулярной шкалыСодержание книги
Поиск на нашем сайте
1.1. Включить неоновую лампочку в сеть 220 В. 1.2. Часть линейки с миллиметровыми делениями подвести под микроскоп и навести на резкость. При этом в поле зрения должны быть видны две соседние риски, т.е. один миллиметр линейки. 1.3. Подсчитать число делений N (больших или малых) окулярной шкалы, уложившихся между левыми краями изображения рисок, а затем между правыми. Помещая в поле зрения соседние миллиметры линейки, проделать то же самое. 1.4. Рассчитать среднее значение <N> и среднюю цену деления для окулярной шкалы < b > = 1/ <N> в миллиметрах на деление (большое или малое). 1.5. Определить относительную погрешность db = Db / < b >, предварительно установив связь db с относительной погрешностью DN/<N> на основании формулы относительной погрешности при косвенных измерениях (см. теорию погрешностей). D N найти по формуле
при a =... (выбирается экспериментатором). 1.6. Найти абсолютную погрешность Db и записать результат измерения D в виде доверительного интервала. Результаты измерений и вычислений занести в табл. 1. Определение радиуса кривизны линзы Подвести кольца Ньютона под объектив микроскопа и "поймать" их в окуляр. Для этого следует перемещать пластинку с линзой в горизонтальных направлениях, а тубус микроскопа - вверх и вниз. Чтобы свет от лампочки попадал в микроскоп после отражения от границ воздушного слоя между линзой и пластинкой, последние Таблица 1
расположены наклонно к оси микроскопа. В результате этого кольца Ньютона видны в виде эллипсов. Понятно, что истинному диаметру кольца соответствует большая ось эллипса, вдоль которой и следует расположить окулярную шкалу. 2.2. Произвести отсчеты х 1 и х 2 положений диаметрально противоположных точек середин темных (светлых) колец Ньютона, вычислить диаметры колец и их квадраты. 2.3. Выбрать номера колец i и m, наиболее далекие друг от друга для избежания больших погрешностей, рассчитать для каждой пары 2.4. Как следует из вышесказанного, диаметр кольца Ньютона можно непосредственно измерить в делениях окулярной шкалы. Умножая этот результат на величину b, выраженную в мм/дел., получим диаметр в миллиметрах. Из формулы (7.9) выразим радиус кривизны линзы:
где диаметр D выражен в тех же делениях окулярной шкалы (в больших или в малых), что и N. Усредненная длина волны света неоновой лампочки l = (640 + 30) нм. В целях упрощения расчетов величину R = По формуле (7.12) определить <R> 2.5. Подсчитать абсолютную погрешность:
гдеD T найти по формуле, аналогичной формуле (7.13). 2.6. Результаты измерений и вычислений занести в табл. 2. Записать окончательный результат в виде доверительного интервала с указанием надежности и относительной погрешности. Таблица 2
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Явление интерференции света. 2. Когерентность. 3. Оптическая длина пути и оптическая разность хода. 4. Условия максимумов и минимумов при интерференции. 5. Явления, происходящие при отражении: от среды, оптически более плотной; от среды, оптически менее плотной. 6. Линии равной толщины. Кольца Ньютона. 7. Вывод расчетной формулы. 8. Ход эксперимента по определению радиуса кривизны линзы или длины волны света с помощью колец Ньютона. 9. Вычисления погрешностей измерений.
ЛАБОРАТОРНАЯ РАБОТА № 8 ИЗУЧЕНИЕ ЯВЛЕНИЯ ДИФРАКЦИИ СВЕТА С ПОМОЩЬЮ ДИФРАКЦИОННОЙ РЕШЕТКИ
Цель работы: изучить явление дифракции в монохроматическом свете при помощи дифракционной решетки и щели. Приборы и принадлежности: лазер, дифракционная решетка (или щель), измерительная линейка и экран. Сведения из теории
Дифракцией света называют явления, вызванные нарушением цельности волновой поверхности. Дифракция проявляется в нарушении прямолинейности распространения колебаний. Волна огибает края препятствия и проникает в область геометрической тени. Дифракционные явления присущи всем волновым процессам, но проявляются особенно отчетливо лишь в тех случаях, когда длины волн излучений сопоставимы с размером препятствий. С точки зрения представлений геометрической оптики о прямолинейном распространении света граница тени за непрозрачным препятствием резко очерчена лучами, которые проходят мимо препятствия, касаясь его поверхности. Следовательно, явление дифракции необъяснимо с позиций геометрической оптики. По волновой теории Гюйгенса, рассматривающей каждую точку поля волны как источник вторичных волн, распространяющихся по всем направлениям, в том числе и в область геометрической тени препятствия, вообще неясно, как может возникнуть сколько-нибудь отчетливая тень. Тем не менее, опыт убеждает нас в существовании тени, но не резко очерченной, как утверждает теория прямолинейного распространения света, а с размытыми краями. Причем в области размытости наблюдается система интерференционных максимумов и минимумов освещенности.
Принцип Гюйгенса – Френеля Особенность дифракционных эффектов состоит в том, что дифракционная картина в каждой точке пространства является результатом интерференции лучей от большого числа вторичных источников Гюйгенса. Объяснение этих эффектов было осуществлено Френелем и получило название принципа Гюйгенса - Френеля. Сущность принципа Гюйгенса - Френеля можно представить в виде нескольких положений: 1. всю волновую поверхность, возбуждаемую каким-либо источником S 0площадью S, можно разбить на малые участки с равными площадями dS, которые будут являться системой вторичных источников, испускающих вторичные волны; 2. эти вторичные источники, эквивалентные одному и тому же первичному источнику S 0, когерентны между собой. Поэтому волны, распространяющиеся от источника S 0, в любой точке пространства должны являться результатом интерференции всех вторичных волн; 3. мощности излучения всех вторичных источников - участков волновой поверхности с одинаковыми площадями – одинаковы; 4. каждый вторичный источник (с площадью dS) излучает преимущественно в направлении внешней нормали n к волновой поверхности в этой точке; амплитуда вторичных волн в направлении, составляющем с n угол a, тем меньше, чем больше угол a, и равна нулю при a ³ (p / 2); 5. амплитуда вторичных волн, дошедших до данной точки пространства, зависит от расстояния вторичного источника до этой точки: чем больше расстояние, тем меньше амплитуда; 6. когда часть волновой поверхности S прикрыта непрозрачным экраном, вторичные волны излучаются только открытыми участками этой поверхности. При этом часть световой волны, закрытая непрозрачным экраном, не действует совсем, а открытые области волны действуют так, как если бы экрана совсем не было; Принцип Гюйгенса - Френеля позволяет объяснить явление дифракции и дать методы ее количественного расчета. Различают два случая дифракции. Если преграда, на которой происходит дифракция, находится вблизи от источника света или от экрана, на котором производится наблюдение, то фронт падающих или дифрагированных волн имеет криволинейную поверхность; этот случай называется дифракцией Френеля или дифракцией в расходящихся лучах. Если падающие и дифрагированные волны плоские, явление значительно упрощается; этот частный случай называется дифракцией Фраунгофера или дифракцией в параллельных лучах. Плоские волны получаются либо удалением источника света и места наблюдения от преграды, вызывающей дифракцию, либо применением соответственного расположения линз. Метод зон Френеля Дифракция Френеля играет основную роль в волновой теории, ибо, вопреки принципу Гюйгенса и на основе принципа Гюйгенса - Френеля, объясняет прямолинейность распространения света в свободной от препятствий однородной среде. Чтобы показать это, рассмотрим действие сферической световой волны от точечного источника S0 в произвольной точке пространства P (рис. 8.1). Волновая поверхность такой волны
Рис. 8.1.
симметрична относительно прямой S 0 P. Амплитуда искомой волны в точке P зависит от результата интерференции вторичных волн, излучаемых всеми участками dS поверхности S. Амплитуды и начальные фазы вторичных волн зависят от расположения соответствующих источников dS по отношению к точке P. Воспользовавшись симметрией задачи, Френель предложил оригинальный метод разбиения волновой поверхности на зоны (метод зон Френеля). По этому методу волновая поверхность разбивается на кольцевые зоны (рис.8.1), построенные так, что расстояния от краев каждой зоны до точки P отличаются на l/2 (l - длина световой волны в той среде, в которой распространяется волна). Если обозначить через r 0 расстояние от вершины волновой поверхности 0 до точки P, то расстояния r 0 + k (l/2) образуют границы всех зон, где k - номер зоны. Колебания, приходящие в точку P от аналогичных точек двух соседних зон, противоположны по фазе, так как разность хода от этих зон до точки P равна l /2. Поэтому при наложении эти колебания взаимно ослабляют друг друга, и результирующая амплитуда выразится суммой: A = A 1- A 2 + A 3 - A 4 +.... (8.1) Величина амплитуды A kзависит от площади D S k k -й зоны и угла a kмежду внешней нормалью к поверхности зоны в любой ее точке и прямой, направленной из этой точки в точку P. Можно показать, что площадь D S k k -й зоны не зависит от номера зоны в условиях l << r 0. Таким образом, в рассматриваемом приближении площади всех зон Френеля равновелики и мощность излучения всех зон Френеля - вторичных источников - одинакова. Вместе с тем, с увеличением k возрастает угол akмежду нормалью к поверхности и направлением в точку P, что приводит к уменьшению интенсивности излучения k -й зоны в данном направлении, т.е. к уменьшению амплитуды A k по сравнению с амплитудами предыдущих зон. Амплитуда A k уменьшается также вследствие увеличения расстояния от зоны до точки P с ростом k. В итоге A 1 > A 2 > A 3 > A 4 >... > A k >... Вследствие большого числа зон убывание Ak носит монотонный характер и приближенно можно считать, что
Переписав (8.1) в виде
обнаруживаем, что, согласно (8.2) и с учетом малости амплитуды удаленных зон, все выражения в скобках равны нулю и уравнение (8.1) приводится к виду A = A 1 / 2.(8.4) Полученный результат означает, что колебания, вызываемые в точке P сферической волновой поверхностью, имеют такую же амплитуду, как если бы действовала только половина центральной зоны Френеля. Следовательно, свет от источника S 0 в точку P распространяется как бы в пределах очень узкого прямого канала, т.е. прямолинейно. Мы приходим к выводу, что в результате явления интерференции уничтожается действие всех зон, кроме первой.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 374; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.23.110 (0.006 с.) |

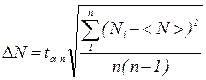 (7.10)
(7.10) и T.
и T. , (7.11)
, (7.11) обозначим через T. Тогда
обозначим через T. Тогда (7.12)
(7.12) , (7.13)
, (7.13)
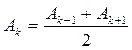 . (8.2)
. (8.2) , (8.3)
, (8.3)


