
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение ЭДС источника токаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Кафедра общей физики
ФИЗИКА Лабораторный практикум для студентов – заочников Всех специальностей
Пермь 2002
План УМД 2001/2002 уч. г.
ФИЗИКА. Лабораторный практикум для студентов – заочников всех специальностей/Перм. гос. техн.ун-т, Пермь, 2002, - 70 с. Составители: Н.А. Вдовин, к.ф.-м.н., доцент, В.Н. Зайцев, ст. преподаватель, В.А. Лощилова, ассистент, Т.Д. Марценюк, ассистент, Ю.К. Щицина, ст. преподаватель. Под общей ред. д.т.н., профессора Цаплина А.И. Практикум включает в себя 9 лабораторных работ. В начале каждой работы даны краткие теоретические сведения, а в конце - вопросы для самоконтроля. Указан порядок выполнения работ. Практикум предназначен для студентов заочной формы обучения.
Рецензент: канд. физ.-мат. наук, доцент К.Н. Лоскутов.
ÓПермский государственный технический университет, СОДЕРЖАНИЕ
Введение............................................................................................. 4 1.Обработка результатов измерений на примере задачи определения объема цилиндра..................... 5 2. Маятник Обербека....................................................................... 15 3. Физический маятник....................................................................... 22 4. Исследование электростатических полей................................... 27 Определение ЭДС источника тока компенсационным методом.......................................................... 32 6. Определение магнитной индукции в межполюсном зазоре прибора магнитоэлектрической системы.................................... 36 7. Определение радиуса кривизны линзы с помощью колец Ньютона........................................................... 42 8. Изучение явления дифракции света с помощью дифракционной решетки........................................... 47 9. Исследование фотоэлементов....................................................... 60 Приложения........................................................................................ 66
ВВЕДЕНИЕ Лабораторные работы являются неотъемлемой частью изучения курса физики. При их выполнении студент воспроизводит некоторые физические явления, учится обращению с основными физическими приборами и методами измерений, приобретает навыки ведения лабораторного журнала, построения графиков, оценки достоверности полученных результатов и оформления отчета. Распределение объемов занятий и видов учебной работы при изучении физики для студентов-заочников всех специальностей дано в табл. 1. Таблица 1
Основной формой подготовки к лабораторным работам является самостоятельная работа студента по изучению предлагаемого материала. Целесообразно проработать материал, пользуясь списком вопросов к каждой лабораторной работе.
СПИСОК ЛИТЕРАТУРЫ
Основная
1. Трофимова Т.И. Курс физики: Учебное пособие.-7 изд., испр.-М.: Высш. шк,2001.-542 с. Дополнительная
2. Савельев И.В. Курс общей физики. М.: Наука,1988. Т.1-3. 3. Детлаф А.А., Яворский Б.М. Курс физики. М.: Высш. шк., 1989. 4. Лабораторный практикум по физике. Под ред. К.А. Барсукова и Ю.И. Уханова. М.: Высш шк., 1988.
ЛАБОРАТОРНАЯ РАБОТА № 1
Обработка результатов измерений на примере задачи определения обьема цилиндра Цель работы: ознакомиться с методом обработки результатов измерений. Приборы и принадлежности: цилиндр, штангенциркуль, микрометр.
Теоретические сведения
Каждая лабораторная работа физического практикума связана с измерениями тех или иных физических величин. Под измерением понимается сравнение измеряемой величины с другой величиной, принятой за единицу измерения. Различают измерения прямые и косвенные. Прямые - это измерения, которые производятся с помощью приборов, непосредственно дающих значение измеряемой величины (длины - линейкой, штангенциркулем; времени - секундомером; силы тока - амперметром и т.д.) Косвенныe - это измерения, при которых неизвестная величина определяется по результатам прямых измерений других величин, с которыми она связана определенной формулой, например, плотность вещества r вычисляют через измеренные m - массу и V – объем тела по формуле r = m /V; электросопротивление проводника R - через измеренные напряжение U и силу тока I по формуле I = U/R и т.д. При измерениях любой величины мы никогда не получаем ее истинного значения. Это объясняется принципиальной невозможностью устранить все посторонние влияния на процесс измерения. Иначе говоря, при всяких измерениях мы допускаем ошибки; их величину принято характеризовать абсолютной погрешностью измерений D x (cм. ниже) и относительной погрешностью e. Эти характеристики не являются независимыми. На способах определения D х подробно остановимся ниже. Что же касается e, то относительной погрешностью измерений называют отношение абсолютной погрешности к истинному значению измеряемой величины
Так как х0 - величина неизвестная, то на практике x0 заменяют найденным из опыта среднеарифметическим значением < x >, поэтому
Относительную погрешность часто выражают в процентах. Таким образом, задача всякого измерения состоит из нахождения наиболее вероятного значения измеряемой величины и оценки абсолютной и относительной погрешности.
Прямые измерения 1. Вычислить среднее значение для n измерений
2. Найти погрешности отдельных измерений 3. Вычислить квадраты погрешностей отдельных измерений и их сумму: 4. Задать надежностьa (для наших целей принимаем a= 0,95) и по таблице определить коэффициенты Стьюдента t a,nи ta,¥. 5. Произвести оценку систематических погрешностей: приборной D хпр и ошибки округления при измеренияхD х окр= D/2 (D - цена деления прибора) и найти полную погрешность результата измерений (полуширину доверительного интервала):
6. Оценить относительную погрешность
7. Окончательный результат записать в виде
Косвенные измерения
1. Для каждой величины, измеренной прямым способом, входящей в формулу для определения искомой величины 2. Определить среднее значение искомой величины z = f (<a>,<b>,<c>,...).
3. Оценить полуширину доверительного интервала для результата косвенных измерений
где производные 4. Определить относительную погрешность результата
5. Если зависимость z от a, b, c,... имеет вид
а затем абсолютную 6. Окончательный результат записать в виде z = <z> ± Dz...% при a =. Примечание: При обработке результатов прямых измерений нужно следовать следующему правилу: численные значения всех рассчитываемых величин должны содержать на один разряд больше, чем исходные (определенные экспериментально) величины. При косвенных измерениях вычисления В окончательной записи абсолютной погрешности следует оставлять только одну значащую цифру. (Если этой цифрой окажется 1 или 2, то после нее сохраняют еще одну цифру). Среднее значение округляется до того же результата, что и абсолютная погрешность. Например: V = I = Порядок выполнения работы Определение диаметра цилиндра. 1. Микрометром или штангенциркулем измерить не менее 7 раз (в разных местах и направлениях) диаметр цилиндра. Результаты записать в таблицу. 2. Вычислить среднее значение диаметра <d> = где n - число измерений, i - номер измерения. 3. Вычислить D di = (di - <d>), D di2 и
4. Задавшись надежностью a (от 0,90 до 0,97), по таблице выбрать коэффициенты Стьюдента t a,n и t a,¥. 5. Определить приборную погрешность D d пр. Для микрометраD d пр = D/2 (D - цена деления микрометра, равная обычно 0,01 мм). Для штангенциркуля D d пр = D, D - “цена” деления нониуса. 6. Вычислить абсолютную ошибку (полуширину доверительного интервала) в определении диаметра цилиндра:
7. Вычислить относительную погрешность e d = D d/<d>.
Определение высоты цилиндра Все измерения и вычисления, выполненные при определении диаметра цилиндра, повторить при той же надежностиa для высоты цилиндра h. Результаты записать в таблицу.
Определение объема цилиндра 1. Вычислить среднее значение объема цилиндра <V> = p/4 <d>2 <h>. 2. Вычислить относительную погрешность определения объема
3. Вычислить полуширину доверительного интервала D V = ev <V>. 4. Результаты записать в виде V =<V> ± D V приa =... ev =...%,.
ЛАБОРАТОРНАЯ РАБОТА № 2 МАЯТНИК ОБЕРБЕКА
Цель: познакомиться с динамическими характеристиками вращательного движения твердого тела, а также с использованием основного закона динамики вращательного движения. Приборы и принадлежности: маятник Обербека, секундомер, мерительная линейка, штангенциркуль. Описание установки и метода определения момента инерции Маятник Обербека представляет собой крестовину, состоящую из втулки 1, четырех спиц 2, укрепленных на одном из концов втулки. На спицах размещены грузы 3. Последние могут перемещаться вдоль спиц и закрепляться на них с помощью винтов. Другой конец втулки выполнен в виде шкива 4, на который наматывается нить-шнур. К свободному концу шнура привязан груз 5. Под влиянием этого груза маятник приходит в ускоренное вращательное движение вокруг неподвижной оси. Трение между втулкой маятника и осью практически сведено к нулю установленными на ось подшипниками. Для установки груза 5 на определенной высоте предусмотрен указатель 6. Исходным уравнением для определения момента инерции I маятника является уравнение (2.11), из которого следует, что
М = T R, (2.13) где R - радиус шкива. Сила T может быть найдена из второго закона Ньютона. записанного для груза 5: ma = mg - T, где m - масса груза 5; а - ускорение, с которым он опускается, откуда Т = m (g - а). (2.14) Таким образом, подставляя (2.14) в (2.13), получим М = m(g - a) R. (2.15) Угловое ускорение e связано с тангенциальным ускорением
В свою очередь,
Ускорение а можно вычислить, если измерить время t опускания груза 5 на определенную высоту h. Действительно
а потому
Подставляя (2.17) в (2.16) и (2.15), а затем в (2.12), получим
где d = 2 R - диаметр шкива. Заметим, однако, что второе слагаемое в выражении (2.18) оказывается на практике значительно меньше первого, а потому момент инерции маятника можно вычислить как
Формула (2.19) - рабочая формула для определения I из законов динамики. С другой стороны, как уже отмечалось, момент инерции тела - величина аддитивная. Следовательно, момент инерции маятника Обербека относительно оси вращения можно представить в виде
I = I в + I ш + 2 I сп + 4I гр, (2.20)
где: I в - момент инерции втулки; I ш - момент инерции шкива; I сп- момент инерции спицы; I гр - момент инерции одного груза 3. (Разумеется, все эти моменты инерции в данном случае берутся тоже относительно оси вращения.) Так как где l и m пс- общая длина (рис.2.5) и масса двух спиц, а для случая, когда грузы 3 находятся на концах спиц, I гр = m гр l 12 (груз - материальная точка), где l 1- расстояние от центра масс груза до оси, а m гр - масса груза 3, то
I = (I в + I ш ) + 1/6 × m пс l2 + 4 m гр l 12. (2.21)
Порядок выполнения работы
1. Внесите в таблицу данные о массе груза 5 и ускорении свободного падения для широты г. Пермь (написаны на приборе). 2.Установите грузы 4 на концы спиц, причем так, чтобы маятник находился в безразличном равновесии. 3. Наматывая нить на шкив, установите груз 5 так, чтобы основание груза совпало с указателем 6 (см. рис.2.4), (следите за тем, чтобы витки нити на шкив наматывались в один слой, а нить намоталась бы с внешней стороны маятника). В этом положении маятник придерживайте рукой за одну из спиц. 4. Измерьте время t 1падения груза 5 с установленной высоты до пола. Для чего отпустите маятник без толчка, включив одновременно секундомер. Опыт повторите не менее 7 раз. Результаты занесите в таблицу. 5. Передвиньте грузы 3 примерно на середину спиц и установите их так, чтобы маятник находился в безразличном равновесии. По п. 4 измерьте время t 2 движения груза в этом случае. Результаты запишите в таблицу. 6. Измерьте диаметр шкива d и высоту падения груза h, оцените ошибкиD d иD h в измерении этих величин. Данные занесите в таблицу. 7. Вычислите < < I > = вычислите среднее значение моментов инерции 8. Определите абсолютную и относительную погрешности в определении момента инерции (только для Для чего:
а) задайтесь надежностью a (от 0,90 до 0,97), выберите коэффициент Стьюдента б) вычислите абсолютную погрешность в измерении времени:
в) вычислите относительную погрешность в определении I (например, I
г) вычислите абсолютную погрешность:
д) результаты запишите в виде
9. Сравнивая I 10. Измерьте l и l 11. Найдите расхождение в процентах между значениями I 1 и I 1ад, полученными из опыта и вычисленными по формуле (2.21). КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что называется моментом инерции материальной точки относительно оси, моментом инерции твердого тела относительно оси? В каких единицах измеряется момент инерции? 2. В чем состоит теорема Штейнера? Приведите пример ее использования. 3. Что называется моментом силы относительно оси? В каких единицах он измеряется? 4. Что такое плечо силы? 5. Что называется моментом импульса материальной точки относительно оси вращения, моментом импульса твердого тела относительно оси вращения? В каких единицах измеряется момент импульса? 6. Как связаны между собой момент импульса и момент инерции тела, вычисленные относительно оси вращения? 7. Маятник Обербека: устройство и теория метода определения его инерции. 8. Порядок выполнения работы. Выводы.
ЛАБОРАТОРНАЯ РАБОТА № 3 ФИЗИЧЕСКИЙ МАЯТНИК Цель: познакомиться с методом определения моментов инерции тел. Приборы и принадлежности: исследуемое тело (пластина), кронштейн для подвешивания тела, секундомер, линейка, математический маятник. Описание установки и метода определения инерции тела
Исследуемое тело 1 представляет собой металлическую пластину с двумя вырезами (рис. 3.2). Этими вырезами тело подвешивается на опору - кронштейн 2 для организации колебаний. Чтобы уменьшить трение и износ детали точки подвеса О1 и О2 снабжены специальными подставками 3. На конце кронштейна может быть подвешен математический маятник 4, длину которого можно изменять. В работе определяются моменты инерции I 1 и I 2относительно осей О1 и О2. Метод определения моментов инерции основан на том, что период колебаний ФМ (пластина в данном случае играет роль физического маятника) связан с его моментом инерции относительно оси колебания (см. формулу (3.8)). Таким образом, измерив на опыте период колебаний маятника Т и расстояние b от точки подвеса до центра масс (см. рис.3.1), зная массу m маятника и ускорение свободного падения g, можно вычислить момент инерции:
Порядок выполнения работы
1. Снять пластину с подвеса, измерить линейкой расстояния b1 = O1C и b2 = O2C (см. рис. 3.2) и оценить ошибку D b этих измерений. Результаты занести в табл.1; сюда же вписать данные о массе тела и ускорении свободного падения. 2. Подвесить маятник на ось О1, привести его в движение (j £ 8о) и измерить время t1 для 30-50 полных колебаний (N). (Отсчет времени лучше начинать после того, как тело совершит несколько колебаний). Опыт повторить не менее 5 раз при одном и том же числе колебаний. Результаты (эти и последующие) занести в табл.1. 3. Снять маятник и, подвесив его на ось О2, проделать то же, что и в п.2. 4. Вычислить Т1 и Т2 для каждого из опытов и их средние значения <T1> и <T2>. Таблица 1
5. По формуле
(см. (3.12)) вычислить < I 1 > и <I 2 >. 6. Для момента инерции I 2 вычислить относительную eI2 и абсолютную D I 2 погрешности (для I 1 первую из них принять такой же). Для этого: а) подсчитать Т2i - <Т2>, (T2i - <T2>) 2, б) вычислить абсолютную погрешность в измерении периода колебаний
где n - число измерений; D t пр - приборная погрешность секундомера; t a,n - коэффициент Стьюдента (определяется по таблице в зависимости от выбранной надежности a и n); N – число полных колебаний. в) определить относительную погрешность;
г) вычислить абсолютную погрешность в определении I2: D I 2 = eI <I 2 >; 7. Результаты представить в виде: I 1 = <I1> ± D I 1 I 2 = <I2> ± D I 2 приa =, eI = %. 8. Вычислить приведенные длины L1 и L2 маятников по формуле
9. При наличии математического маятника установить его длину l равной L 1 (или L 2) и убедиться в синхронности колебаний физического и математического маятников.
КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Физический маятник. 2. Уравнения колебаний физического маятника (дифференциальное уравнение и его решение). 3. Частота и период колебаний физического маятника. 4. Приведенная длина физического маятника. 5. Точка подвеса и центр качаний физического маятника. 6. Метод определения I в данной работе. 7. Порядок выполнения работы.
ЛАБОРАТОРНАЯ РАБОТА № 4
ИССЛЕДОВАНИЕ ЭЛЕКТРОСТАТИЧЕСКИХ ПОЛЕЙ
Цель работы: ознакомиться с методом моделирования электростатического поля с помощью электропроводной бумаги; исследовать электростатическое поле плоского и цилиндрического конденсаторов. Приборы и принадлежности: источник постоянного тока, вольтметр, электропроводная бумага, планшет с набором электродов, проводники, один из которых снабжен зондом.
Сведения из теории
Электростатическое поле (ЭСП) - форма материи, осуществляющая взаимодействие между заряженными телами. Основным свойством поля является его силовое действие на любой заряд, помещенный в поле. Источником ЭСП является неподвижный заряд (заряженное тело). Количественными характеристиками ЭСП являются напряженность и потенциал. Напряженность поля - векторная физическая величина, характеризующая силовое действие поля в точке, численно равная силе, с которой поле действовало бы на положительный единичный заряд, помещенный в данную точку поля и по направлению совпадающая с направлением действия этой силы.
здесь Таким образом, напряженность - это силовая характеристика поля. Единица напряженности - Н/Кл (В/м). Если напряженность поля во всех точках одинаковапо величине и направлению, то поле называют однородным, в противном случае - неоднородным. Потенциал поля в точке -это скалярная физическая величина, характеризующая энергетические свойства поля, численно равная потенциальной энергии положительного единичного заряда, помещенного в данную точку поля.
здесь Wп - потенциальная энергия заряда +q, помещенного в некоторую точку поля. Единицей потенциала является В (Дж/Кл). Потенциал - энергетическая характеристика поля. Потенциальная энергия, а вместе с ней и потенциал задаются с точностью до постоянной. Чтобы потенциал приобрел вполне определенное значение, надо придать ему некоторое значение в одной из точек поля. В физике принято считать j = 0 в точке, удаленной бесконечно далеко от заряженного тела. Надо, однако, помнить, что хотя для любой точки поля можно указать такую величину, как потенциал, ясный физический смысл имеет только разность потенциалов двух точек поля (j1 - j2 ): она равна работе поля по перемещению единицы положительного заряда из одной точки (1) в другую (2). Измерить практически можно тоже только разность потенциалов. И, говоря об измерении потенциала, подразумевают измерение разности потенциалов двух точек, потенциал одной из которых условно принимается за нуль. Из определения разности потенциалов двух точек поля следует, что работа поля по перемещению заряда +q из точки 1 в точку 2 может быть вычислена по формуле А = q (j1 - j2). (4.3) Электростатическое поле можно изобразить графически. Делается это с помощью линий напряженности (силовых линий) и эквипотенциальных поверхностей. Линией напряженности называется линия, касательная к которой в каждой точке совпадает с направлением напряженности поля в этой точке (рис. 4.1 - сплошные кривые).
Рис. 4.1
Эквипотенциальная поверхность - поверхность равного потенциала (на рис. 4.1 пунктирные линии - линии пересечения этих поверхностей с плоскостью рисунка). Так как работа поля по перемещению заряда вдоль эквипотенциальной поверхности равна нулю (j1 = j2), то это значит, что линии напряженности в любой точке поля перпендикулярны эквипотенциальным поверхностям. Напряженность и разность потенциалов поля связаны между собой. В общем случае эта связь выглядит так:
Здесь производная по расстоянию берется вдоль линии напряженности в направлении, совпадающем с направлением единичного вектора нормали n к эквипотенциальной поверхности. Из уравнений (4.4) видно, что вектор E всегда направлен в сторону уменьшения потенциала. В случае однородного поля модуль вектора напряженности связан с разностью потенциалов соотношением:
где jА и j В - потенциалы двух точек (А и В), лежащих на одной линии напряженности, а d - расстояние между этими точками. Таким образом, зная закон изменения потенциала вдоль силовой линии, можно в любой точке поля определить напряженность поля, численное значение которой равно изменению потенциала на единице длины силовой линии. Отсюда следует еще одна единица измерения напряженности - B/м.
Рис. 4.2 2) на бумаге для указанных выше полей провести эквипотенциальные линии и линии напряженности; 3) вычислить величину напряженности поля плоского конденсатора; построить график зависимости потенциала от расстояния. Порядок выполнения работы
1. Путем осмотра познакомиться с приборами и принадлежностями. Установить предел измерения вольтметра, определить “цену” деления прибора. 2. Закрепить оба листа электропроводной бумаги на планшете темной графитовой стороной вверх, плотно прижав к ним обе пары металлических электродов. Контуры электродов обвести. 3. На прямолинейных электродах собрать электрическую цепь (см. рис.4.2) и после проверки подключить к источнику постоянного тока. 4. С помощью зонда проверить: на который из электродов подан более высокий потенциал (желательно “минус” - на левый). На бумаге пометить электроды знаками “+” и “-”. 5. Экспериментально найти 5-6 групп точек поля, каждая из которых (групп) имеет одинаковый потенциал. Начните с точек, лежащих на расстоянии 5-10 мм от “-” электрода. В каждой группе взять по 8-10 точек, в том числе во внешней для конденсатора области. Точки на бумаге отмечают прижатием зонда к бумаге. Показания вольтметра для каждой из групп (j1, j2, j3 ,...) занести в табл. 1. 6. Перенести электрическую цепь на цилиндрические электроды. Подключить источник тока, установить полярность электродов и найти 2-3 группы точек с одинаковыми потенциалами, значения которых записать прямо на бумаге. Источник поля отключить, цепь разобрать. 7. Оба листа бумаги снять. Повернуть (хотя и не обязательно) светлой стороной вверх. Отметить положение электродов, поставив знаки “+” и “-”. Точки с одинаковыми потенциалами соединить. Это и есть эквипотенциальные линии. На том и другом листе провести (по всему полю) по 7-10 линий напряженности, указав их направление. 8. Вычислить напряженность поля плоского конденсатора и построить графикDji1 = f ( D ri1): а) вычислить разность потенциалов Dj21 = j2-j1, Dj31 = j3-j1 ,...; б) по одной из линий напряженности (в средней части поля) измерить расстоянияD r 21, D r 31,...; все результаты занести в табл. 1; Таблица 1
в) по формуле (4.5), по данным п.п. “а”,“б” вычислить значения напряженностей исследуемого поля и по ним среднее значение <Е>; г) заполнить другие графы таблицы, т. е. вычислить Dji1×D r i1, D ri 2, а также S Dji1×D r i1и S Dr i2; д) вычислить напряженность поля по формуле, следующей из метода наименьших квадратов:
е) сравнить результаты п.п. “в” и “д”. Найти расхождение в процентах между < E > и E, т. е. расхождение одной и той же величины, найденной разными способами; ж) начертить график зависимости разности потенциалов (потенциала) от расстояния Dji1 = f ( D r r1). Сделать соответствующий вывод. 9. Рабочее место привести в порядок и сдать лаборанту.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Что такое ЭСП? В чем состоит его основное свойство? 2. Какими величинами характеризуют ЭСП? 3. Что называют напряженностью поля? Единицы ее измерения. 4. Что называется потенциалом данной точки поля? Единицы его измерения. 5. Каков физический смысл разности потенциалов двух точек поля? 6. Какова связь между напряженностью и потенциалом поля, между напряженностью и разностью потенциалов? 7. Как графически изображается ЭСП? 8.Что такое линии напряженности и эквипотенциальные поверхности поля? Каково их взаимное расположение (при изображении поля)? 9. Ка
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 638; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.253.21 (0.012 с.) |


 .
.
 . (1.1)
. (1.1) .
. .
. .
. .
. 100 %.
100 %. % при a =...
% при a =... , провести обработку, как указано выше. Если среди величин a, b, c,... есть табличные константы или числа типа p, е,..., то при вычислениях
, провести обработку, как указано выше. Если среди величин a, b, c,... есть табличные константы или числа типа p, е,..., то при вычислениях  округлять их следует так (если это возможно), чтобы вносимая при этом относительная ошибка была на порядок меньше наибольшей относительной ошибки величин, измеренных прямым способом.
округлять их следует так (если это возможно), чтобы вносимая при этом относительная ошибка была на порядок меньше наибольшей относительной ошибки величин, измеренных прямым способом. ,
, .......вычисляются при
.......вычисляются при 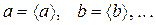
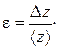 100 %.
100 %. , где k, l, m - любые действительные числа, то сначала следует найти относительную ошибку
, где k, l, m - любые действительные числа, то сначала следует найти относительную ошибку ,
, .
. производить по правилам приближенных вычислений.
производить по правилам приближенных вычислений.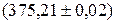 см
см  =
=  см
см  A =
A =  Дж.
Дж.
 .
.
 .
. где ep = Dp/p.
где ep = Dp/p. Сумма
Сумма
 , (2.12)
, (2.12)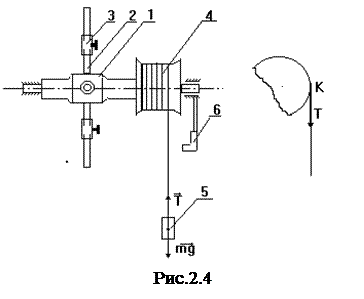 где M - вращающий момент, в данном случае - момент силы Т натяжения шнура, приложенной в точке k (рис.2.4);
где M - вращающий момент, в данном случае - момент силы Т натяжения шнура, приложенной в точке k (рис.2.4);  - угловое ускорение маятника. Момент силы берется относительно оси вращения, а потому
- угловое ускорение маятника. Момент силы берется относительно оси вращения, а потому точек на ободе колеса следующим соотношением:
точек на ободе колеса следующим соотношением: .
. совпадает с ускорением а, с которым опускается груз 5. Следовательно,
совпадает с ускорением а, с которым опускается груз 5. Следовательно, . (2.16)
. (2.16) ,
, . (2.17)
. (2.17) , (2.18)
, (2.18) . (2.19)
. (2.19) ,
,
 > и <
> и <  > и по формуле
> и по формуле ,
, и
и  (для того и другого расположения грузов 3).
(для того и другого расположения грузов 3). или только для
или только для  , так как погрешности будут приблизительно одинаковыми).
, так как погрешности будут приблизительно одинаковыми).
 g = … ± …
d =… ± …
h =… ± …
a =
g = … ± …
d =… ± …
h =… ± …
a =
 D t1 =
D t1 =
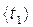 =
=
 =
=
 , оцените D t пр для секундомера;
, оцените D t пр для секундомера;
 ;
;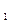 ):
):
 ;
; , при
, при  %,
%, . a =...
. a =... , сделайте вывод (касающийся связи величины момента инерции и расположения грузов 3).
, сделайте вывод (касающийся связи величины момента инерции и расположения грузов 3). (3.12)
(3.12)







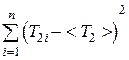 (cм. табл. 1);
(cм. табл. 1); ,
,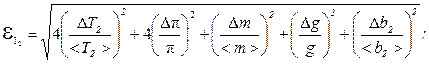

 , (4.1)
, (4.1) - сила, действующая на заряд + q, помещенный в данную точку поля.
- сила, действующая на заряд + q, помещенный в данную точку поля. , (4.2)
, (4.2)

 или
или  . (4.4)
. (4.4)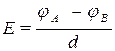 , (4.5)
, (4.5)

 1
1
 Сумма
Сумма
 ; (4.6)
; (4.6)


