
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Абсолютная и относительная погрешностиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть имеется некоторая числовая величина, и числовое значение, которое ей присвоено
Погрешность может принимать как положительное так и отрицательное значение. Величина Абсолютной погрешностью приближенного значения
Качество приближения существенным образом зависит от принятых единиц измерения и масштабов величин, поэтому целесообразно соотнести погрешность величины и ее значение, для чего вводится понятие относительной погрешности. Относительной погрешностью приближенного значения называют величину
Относительную погрешность часто выражают в процентах. Использование относительных погрешностей удобно, в частности, тем, что они не зависят от масштабов величин и единиц измерения. Так как точное значение обычно неизвестно, то непосредственное вычисление величин абсолютной и относительной погрешностей по предложенным формулам невозможно. Более реальная и часто поддающаяся решению задача состоит в получении оценок погрешности вида:
где Если величина
Точно так же если величина
Но поскольку точное значение
В литературе по методам вычислений широко используется термин "точность". Точное значение величины — это значение, не содержащее погрешности. Повышение точности воспринимается как уменьшение погрешности. Часто используемая фраза "требуется найти решение с заданной точностью
Погрешности основных арифметических операций Правило 1: Пусть
Правило 2: Пусть 1. Здесь Первое из равенств означает, что при суммировании чисел одного знака не происходит потери точности, если оценивать точность в относительных единицах. Совсем иначе обстоит дело при вычитании чисел одного знака. Здесь граница относительной ошибки возрастает в При построении численного метода решения задачи следует избегать вычитания близких чисел одного знака. Если же такое вычитание неизбежно, то следует вычислять аргументы с повышенной точностью, учитывая ее потерю примерно Правило 3: Для относительных погрешностей произведения и частного приближенных чисел верны оценки: 1. в последней из которых Приведенные равенства чаще всего используют для практической оценки погрешности. Выполнение арифметических операций над приближенными числами, как правило, сопровождается потерей точности. Единственная операция, при которой потеря не происходит, — это сложение чисел одного знака. Наибольшая потеря точности может произойти при вычитании близких чисел одного знака.
|
|||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 829; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.128.78.107 (0.008 с.) |

 , считается точным, тогда под погрешностью приближенного значения числовой величины (ошибкой)
, считается точным, тогда под погрешностью приближенного значения числовой величины (ошибкой) 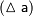 понимают разность между точным и приближенным значением числовой величины:
понимают разность между точным и приближенным значением числовой величины:
 называется известным приближением к точному значению числовой величины - любое число, которое используется вместо точного значения. Простейшей количественной мерой ошибки является абсолютная погрешность.
называется известным приближением к точному значению числовой величины - любое число, которое используется вместо точного значения. Простейшей количественной мерой ошибки является абсолютная погрешность. , про которую известно, что:
, про которую известно, что:
 , про которую известно, что:
, про которую известно, что: .
.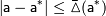
 (*)
(*) и
и  — известные величины, которые называют верхними границами (или просто границами) абсолютной и относительной погрешностей.
— известные величины, которые называют верхними границами (или просто границами) абсолютной и относительной погрешностей.
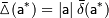
 неизвестно, на практике используют приближенные равенства вида:
неизвестно, на практике используют приближенные равенства вида: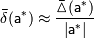
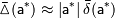
 " означает, что ставится задача о нахождении приближенного решения, принятая мера погрешности которого не превышает заданной величины
" означает, что ставится задача о нахождении приближенного решения, принятая мера погрешности которого не превышает заданной величины  и
и  — приближенные значения чисел
— приближенные значения чисел  , тогда абсолютная погрешность алгебраической суммы (суммы или разности) не превосходит суммы абсолютных погрешностей слагаемых, т.е.[1]:
, тогда абсолютная погрешность алгебраической суммы (суммы или разности) не превосходит суммы абсолютных погрешностей слагаемых, т.е.[1]: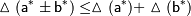
 ; 2.
; 2.  .
. , а
, а  [1].
[1]. раз и возможна существенная потеря точности. Если числа
раз и возможна существенная потеря точности. Если числа  ,то
,то  и не исключена полная или почти полная потеря точности. Когда это происходит, говорят о катастрофической потери точности.
и не исключена полная или почти полная потеря точности. Когда это происходит, говорят о катастрофической потери точности. раз.
раз. ; 2.
; 2.  ;
; [1].
[1].


