
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос 1. Абсолютная и относительные погрешности. Основные источники погрешностей. Действия с приближенными числами.Содержание книги
Поиск на нашем сайте
Вопрос 1. Абсолютная и относительные погрешности. Основные источники погрешностей. Действия с приближенными числами. Источники и классификация погрешностей результата численного решения задачи Приближенным числом или приближением называется число, незначительно отличающееся от точного значения величины и заменяющее его в вычислениях. Под погрешностью же принято понимать разность между абсолютным значением и его приближением. Для правильного понимания подходов и критериев, используемых при решении прикладной задачи с применением ЭВМ, важно понимать, что получить точное значение решения практически невозможно. Получаемое на ЭВМ решение почти всегда (за исключением некоторых весьма специальных случаев) содержит погрешность, т.е. является приближенным. Невозможность получения точного решения следует уже из ограниченной разрядности вычислительной машины. Наличие погрешности обусловлено рядом весьма глубоких причин.
Полная погрешность Появление неустранимой погрешности обусловлено тем, что принятие математической модели и задание исходных данных вносит в решение ошибку, которая не может быть устранена далее. Единственный способ уменьшить эту погрешность — перейти к более точной математической модели и задать более точные исходные данные.
Достоверная информация о порядке величины погрешности метода позволяет осознанно выбрать метод решения задачи и разумно задать его точность. Желательно, чтобы величина погрешности метода была в 2—10 раз меньше неустранимой погрешности. Большее значение ощутимо снижает точность результата, меньшее — обычно требует увеличения затрат, практически уже не влияя на значение полной погрешности. Величина вычислительной погрешности (при фиксированных модели, входных данных и методе решения) в основном определяется характеристиками используемой ЭВМ. Желательно, чтобы эта величина была хотя бы на порядок меньше величины погрешности метода и совсем не желательна ситуация, когда она существенно ее превышает. Погрешности элементарных функций 1. Погрешность функции многих переменных Пусть
Здесь Оценка вытекает из формулы конечных приращений Лагранжа [1]. Для оценки границ относительных погрешностей используют равенство:
Здесь 2. Погрешность неявной функции Нередко приходится сталкиваться с ситуацией, когда функция
Формула Лагранжа
Интерполяционная формула Лагранжа обеспечивает построение алгебраического многочлена Pn (x) для произвольно заданных узлов интерполирования. Для n + 1 различных значений аргумента x 0, x 1,..., xn и соответствующих значений функции f (x 0) = y 0, f (x 1) = y 1,..., f (xn) = yn интерполяционная формула Лагранжа имеет вид
где х - значение аргумента функции, расположенного в интервале [ x 0, xn ]. Необходимо отметить, что формула Лагранжа, в отличие от других интерполяционных формул, содержит явно yi (i =
Пример 1. Построить интерполяционный многочлен Лагранжа для функции, заданной следующей таблицей.
Для случая четырех узлов интерполяции (n = 3) многочлен Лагранжа представляется следующим образом:
Заменив переменные xi, yi (i =
Интерполирование по формуле Лагранжа связано с большим объемом вычислений, значительная часть которых повторяется при получении нескольких значений Pn (x) для одной функции f (x). В том случае, когда формула Лагранжа используется для многократного получения значений одной функции при различных значениях аргумента, можно значительно уменьшить объем вычислений. Для этого формула Лагранжа представляется в виде
где  - лагранжевы коэффициенты, определяемые как - лагранжевы коэффициенты, определяемые как
Вычисление лагранжевых коэффициентов выполняется по следующей схеме, удобной при использовании ЭВМ. Составляется таблица разностей:
Произведение элементов i -й строки обозначается через Ki. Отсюда лагранжевы коэффициенты вычисляются по формуле
где П n +1(x) = (x - x 0)(x - x 1)…(x - xn) - произведение элементов главной диагонали таблицы (эти элементы подчеркнуты). Тогда формула Лагранжапринимает вид:
Использование формулы (2) позволяет сократить значительную часть вычислений по определению лагранжевых коэффициентов Li (n)(x) при различных значениях аргумента. Для этого произведение элементов i -й строки таблицы разностей представляется как Ki = (x – xi) Di, где Di - произведение всех элементов строки, кроме расположенного на главной диагонали. Величина Di (i=
Метод прямоугольников. Различают метод левых, правых и средних прямоугольников. Суть метода ясна из рисунка. На каждом шаге интегрирования функция аппроксимируется полиномом нулевой степени – отрезком, параллельным оси абсцисс.
Выведем формулу метода прямоугольников из анализа разложения функции f(x) в ряд Тейлора вблизи некоторой точки x = xi.
Рассмотрим диапазон интегрирования от xi до xi+h, где h – шаг интегрирования. Вычислим = В случае равного шага h на всем диапазоне интегрирования общая формула имеет вид
Здесь n – число разбиений интервала интегрирования, Для справедливости существования этой оценки необходимо существование непрерывной f'(x). Метод средних прямоугольников. Здесь на каждом интервале значение функции считается в точке
Аппроксимация в этом методе осуществляется полиномом первой степени. Суть метода ясна из рисунка. На единичном интервале
В случае равномерной сетки (h = const)
При этом
Метод Симпсона. Подынтегральная функция f(x) заменяется интерполяционным полиномом второй степени P(x) – параболой, проходящей через три узла, например, как показано на рисунке ((1) – функция, (2) – полином). Рассмотрим два шага интегрирования (h = const = xi+1 – xi), то есть три узла x0, x1, x2, через
Пусть z = x - x0, тогда
Теперь, воспользовавшись полученным соотношением, сосчитаем интеграл по данному интервалу:
В итоге
.Для равномерной сетки и четного числа шагов n формула Симпсона принимает вид:
Здесь вид Формула Симпсона является точной для многочленов до третьей степени включительно. Заметим, что в формуле Симпсона числов узлов обязательно нечетное, то есть n четное, n = 2 m. Вопрос 1. Абсолютная и относительные погрешности. Основные источники погрешностей. Действия с приближенными числами.
|
||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 965; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.193.59 (0.009 с.) |

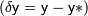 результата решения задачи на ЭВМ складывается из трех составляющих: неустранимой погрешности, погрешности метода и вычислительной погрешности:
результата решения задачи на ЭВМ складывается из трех составляющих: неустранимой погрешности, погрешности метода и вычислительной погрешности:  .
. — дифференцируемая в области
— дифференцируемая в области  функция
функция  переменных, вычисление которой производится при приближенно заданных значениях аргументов
переменных, вычисление которой производится при приближенно заданных значениях аргументов  , тогда для абсолютной погрешности значения
, тогда для абсолютной погрешности значения  справедлива следующая оценка:
справедлива следующая оценка: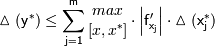
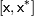 - отрезок, соединяющий точки
- отрезок, соединяющий точки  и
и  : множество точек вида
: множество точек вида  , где
, где  ; а
; а  .
.
 .
.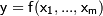 задается не явной формулой, а как решение нелинейного уравнения
задается не явной формулой, а как решение нелинейного уравнения  , т.е. неявно. Если для такой неявной функции воспользоваться известными формулами вычисления производных:
, т.е. неявно. Если для такой неявной функции воспользоваться известными формулами вычисления производных: то исследование неустранимой погрешности неявной функции сразу же сводится к рассмотренному выше случаю.
то исследование неустранимой погрешности неявной функции сразу же сводится к рассмотренному выше случаю. ,
, ), что бывает иногда важно.
), что бывает иногда важно.
 )их числовыми значениями, получим интерполяционный многочлен
)их числовыми значениями, получим интерполяционный многочлен


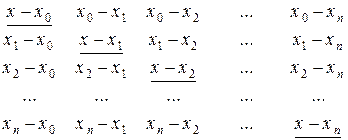


 )не зависит от значения аргумента x и может быть вычислена для заданной функции только один раз.
)не зависит от значения аргумента x и может быть вычислена для заданной функции только один раз.
 …
…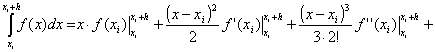 …=
…= =
=  . Получили формулу правых (или левых) прямоугольников и априорную оценку погрешности r на отдельном шаге интегрирования. Основной критерий, по которому судят о точности алгоритма – степень при величине шага в формуле априорной оценки погрешности.
. Получили формулу правых (или левых) прямоугольников и априорную оценку погрешности r на отдельном шаге интегрирования. Основной критерий, по которому судят о точности алгоритма – степень при величине шага в формуле априорной оценки погрешности. .
. .
. , то есть
, то есть  . Разложение функции в ряд Тейлора показывает, что в случае средних прямоугольников точность метода существенно выше:
. Разложение функции в ряд Тейлора показывает, что в случае средних прямоугольников точность метода существенно выше: .
. Метод трапеций.
Метод трапеций. .
.
 , а
, а 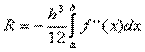 . Погрешность метода трапеций в два раза выше, чем у метода средних прямоугольников! Однако на практике найти среднее значение на элементарном интервале можно только у функций, заданных аналитически (а не таблично), поэтому использовать метод средних прямоугольников удается далеко не всегда. В силу разных знаков погрешности в формулах трапеций и средних прямоугольников истинное значение интеграла обычно лежит между двумя этими оценками.
. Погрешность метода трапеций в два раза выше, чем у метода средних прямоугольников! Однако на практике найти среднее значение на элементарном интервале можно только у функций, заданных аналитически (а не таблично), поэтому использовать метод средних прямоугольников удается далеко не всегда. В силу разных знаков погрешности в формулах трапеций и средних прямоугольников истинное значение интеграла обычно лежит между двумя этими оценками. которые проведем параболу, воспользовавшись уравнением Ньютона:
которые проведем параболу, воспользовавшись уравнением Ньютона: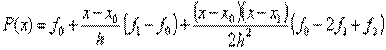 .
.

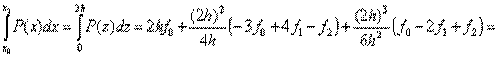
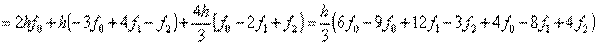 .
.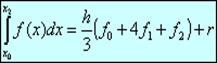

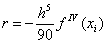 , а
, а  в предположении непрерывности четвертой производной подынтегральной функции.
в предположении непрерывности четвертой производной подынтегральной функции. .
.


