
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритм приближенного вычисления корня методом касательных.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Исходные данные: f (x) – функция; f ‘(x) – производная заданной функции f (x); ε – требуемая точность; x0 – начальное приближение. Результат: xпр – приближенный корень уравнения f (x) = 0. Метод решения: Рассмотрим случай, когда Проведем касательную к кривой y = f (x) в точке В0(b; f(b)). В курсе алгебры выводится уравнение касательной. Уравнение касательной в точке В0 имеет вид Получаем рекуррентную формулу вычисления приближений к корню:
Рис. 8. Геометрическая интерпретация метода касательных для случая Обратим внимание, что в этом случае в качестве начального приближения к корню выбираем точку x0 = b. Приближение к корню происходит с правой стороны, поэтому получаем приближенное значение корня с избытком. Пусть теперь B0
A0
Рис. 9. Геометрическая интерпретация метода касательных для случая Если снова провести касательную к кривой в точке В0, то она пересечет ось Ох в точке не принадлежащей отрезку Получаем рекуррентную формулу вычисления приближений к корню, аналогичную первому случаю:
В данном случае в качестве начального приближения к корню выбираем точку x0 = a. Приближение к коню происходит с левой стороны, поэтому находим приближенное значение корня с недостатком. Заметим, что вычислительные формулы метода отличаются друг от друга только выбором начального приближения: в первом случае за x0 принимаем конец b отрезка, во втором – конец a. Убедитесь сами, что при выборе начального приближения корня можно руководствоваться правилом: за исходную точку следует выбрать тот конец отрезка Условие окончания вычислительного процесса:
Вопрос 7. Интерполирование и экстраполирование. Интерполяционная формула Лагранжа. Интерполяция, интерполирование —способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений. На отрезке [a, b] заданы n + 1 точки x0, x1,..., xn, которые называются узлами интерполяции, и значения некоторой функции f(x) в этих точках f(x0) = y0, f(x1) = y1,..., f(xn) = yn. Требуется построить интерполирующую функцию F(x), принимающую в узлах интерполяции те же значения, что и f(x), т.е. такую, что F(x0) = y0, F(x1) = y1,..., F(xn) = yn. Геометрически это означает, что нужно найти кривую y = F(x) некоторого определенного типа, проходящую через заданную систему точек Mi(xi, yi) для i = В такой общей постановке задача интерполирования может иметь бесчисленное множество решений. Чтобы получить единственную функцию F(x), необходимо предположить, что эта функция не произвольная, а удовлетворяет некоторым дополнительным условиям. Формула Лагранжа
Интерполяционная формула Лагранжа обеспечивает построение алгебраического многочлена Pn (x) для произвольно заданных узлов интерполирования. Для n + 1 различных значений аргумента x 0, x 1,..., xn и соответствующих значений функции f (x 0) = y 0, f (x 1) = y 1,..., f (xn) = yn интерполяционная формула Лагранжа имеет вид
где х - значение аргумента функции, расположенного в интервале [ x 0, xn ]. Необходимо отметить, что формула Лагранжа, в отличие от других интерполяционных формул, содержит явно yi (i = Пример 1. Построить интерполяционный многочлен Лагранжа для функции, заданной следующей таблицей.
Для случая четырех узлов интерполяции (n = 3) многочлен Лагранжа представляется следующим образом:
Заменив переменные xi, yi (i =
Интерполирование по формуле Лагранжа связано с большим объемом вычислений, значительная часть которых повторяется при получении нескольких значений Pn (x) для одной функции f (x). В том случае, когда формула Лагранжа используется для многократного получения значений одной функции при различных значениях аргумента, можно значительно уменьшить объем вычислений. Для этого формула Лагранжа представляется в виде
где  - лагранжевы коэффициенты, определяемые как - лагранжевы коэффициенты, определяемые как
Вычисление лагранжевых коэффициентов выполняется по следующей схеме, удобной при использовании ЭВМ. Составляется таблица разностей:
Произведение элементов i -й строки обозначается через Ki. Отсюда лагранжевы коэффициенты вычисляются по формуле
где П n +1(x) = (x - x 0)(x - x 1)…(x - xn) - произведение элементов главной диагонали таблицы (эти элементы подчеркнуты). Тогда формула Лагранжапринимает вид:
Использование формулы (2) позволяет сократить значительную часть вычислений по определению лагранжевых коэффициентов Li (n)(x) при различных значениях аргумента. Для этого произведение элементов i -й строки таблицы разностей представляется как Ki = (x – xi) Di, где Di - произведение всех элементов строки, кроме расположенного на главной диагонали. Величина Di (i=
|
|||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 860; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.8.172 (0.007 с.) |

 , т.е.
, т.е.  и
и 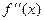 имеют одинаковые знаки. Тогда возможны два случая построения кривой на отрезке
имеют одинаковые знаки. Тогда возможны два случая построения кривой на отрезке 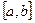 (рис 8).
(рис 8). . В качестве очередного приближения к корню уравнения берем точку пересечения касательной с осью Оx. Полагая y = 0, найдем
. В качестве очередного приближения к корню уравнения берем точку пересечения касательной с осью Оx. Полагая y = 0, найдем  . Теперь
. Теперь  . Применяя метод еще раз для отрезка
. Применяя метод еще раз для отрезка 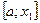 , получим
, получим  .
. (3)
(3)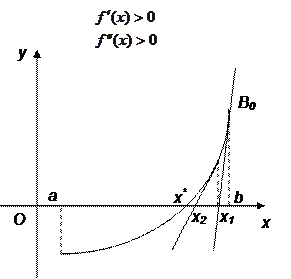

 , т.е.
, т.е. 

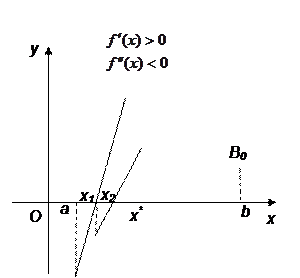

 . Ее уравнение
. Ее уравнение 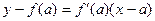 . Находим x1, полагая y = 0:
. Находим x1, полагая y = 0:  . Корень
. Корень  . Применяя метод еще раз для отрезка
. Применяя метод еще раз для отрезка 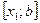 , получим
, получим  , где ε - заданная точность. Тогда xпр = xn+1 с точностью ε.
, где ε - заданная точность. Тогда xпр = xn+1 с точностью ε. . Полученная таким образом интерполяционная формула y = F(x) обычно используется для вычисления значений исходной функции f(x) для значений аргумента x, отличных от узлов интерполяции. Такая операция называется интерполированием функции f(x). При этом различают интерполирование в узком смысле, когда x принадлежит интервалу [x0, xn], и экстраполирование, когда x не принадлежит этому интервалу.
. Полученная таким образом интерполяционная формула y = F(x) обычно используется для вычисления значений исходной функции f(x) для значений аргумента x, отличных от узлов интерполяции. Такая операция называется интерполированием функции f(x). При этом различают интерполирование в узком смысле, когда x принадлежит интервалу [x0, xn], и экстраполирование, когда x не принадлежит этому интервалу. ,
, ), что бывает иногда важно.
), что бывает иногда важно.
 )их числовыми значениями, получим интерполяционный многочлен
)их числовыми значениями, получим интерполяционный многочлен


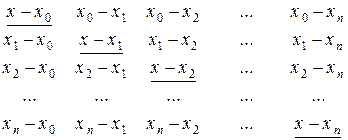


 )не зависит от значения аргумента x и может быть вычислена для заданной функции только один раз.
)не зависит от значения аргумента x и может быть вычислена для заданной функции только один раз.


