
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос 9. Численное интегрирование. Квадратурные формулы прямоугольников, трапеций, формула Симпсона.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Задача численного интегрирования состоит в замене исходной подынтегральной функции f(x), для которой трудно или невозможно записать первообразную в аналитике, некоторой аппроксимирующей функцией φ(x). Такой функцией обычно является полином (кусочный полином)
где Заменяя подынтегральную формулу каким-либо интерполяционным многочленом, мы получаем квадратурные формулы вида:
где xk - выбранные узлы интерполяции, Ak - коэффициенты, зависящие только от выбора узлов, но не от вида функций (k = 0,1,..., n), R - остаточный член, или погрешность квадратурной формулы. Отбрасывая остаточный член R, мы совершаем погрешность усечения. При расчете к ней добавляются различные погрешности округления. Разобьём отрезок интегрирования [ a, b ] на n равных частей системой точек yi = f (xi)(i = 0,1,..., n). Квадратурные формулы для равноотстоящих узлов называются формулами Ньютона-Котеса. Формулы Ньютона-Котеса различаются степенями использованных интерполяционных многочленов. Чтобы не иметь дело с многочленами высоких степеней, обычно разбивают промежуток интегрирования на отдельные участки, применяют формулы Ньютона-Котеса с невысокими степенями на каждом участке и потом складывают полученные результаты. Метод прямоугольников. Различают метод левых, правых и средних прямоугольников. Суть метода ясна из рисунка. На каждом шаге интегрирования функция аппроксимируется полиномом нулевой степени – отрезком, параллельным оси абсцисс.
Выведем формулу метода прямоугольников из анализа разложения функции f(x) в ряд Тейлора вблизи некоторой точки x = xi.
Рассмотрим диапазон интегрирования от xi до xi+h, где h – шаг интегрирования. Вычислим = В случае равного шага h на всем диапазоне интегрирования общая формула имеет вид
Здесь n – число разбиений интервала интегрирования, Для справедливости существования этой оценки необходимо существование непрерывной f'(x). Метод средних прямоугольников. Здесь на каждом интервале значение функции считается в точке
Аппроксимация в этом методе осуществляется полиномом первой степени. Суть метода ясна из рисунка. На единичном интервале
В случае равномерной сетки (h = const)
При этом Метод Симпсона. Подынтегральная функция f(x) заменяется интерполяционным полиномом второй степени P(x) – параболой, проходящей через три узла, например, как показано на рисунке ((1) – функция, (2) – полином). Рассмотрим два шага интегрирования (h = const = xi+1 – xi), то есть три узла x0, x1, x2, через
Пусть z = x - x0, тогда
Теперь, воспользовавшись полученным соотношением, сосчитаем интеграл по данному интервалу:
В итоге
.Для равномерной сетки и четного числа шагов n формула Симпсона принимает вид:
Здесь вид Формула Симпсона является точной для многочленов до третьей степени включительно. Заметим, что в формуле Симпсона числов узлов обязательно нечетное, то есть n четное, n = 2 m.
|
||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1495; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.007 с.) |

 . То есть:
. То есть: ,
, – априорная погрешность метода на интервале интегрирования, а r(x) – априорная погрешность метода на отдельном шаге интегрирования.
– априорная погрешность метода на интервале интегрирования, а r(x) – априорная погрешность метода на отдельном шаге интегрирования.  ,
, , и вычислим подынтегральную функцию в полученных узлах
, и вычислим подынтегральную функцию в полученных узлах
 …
…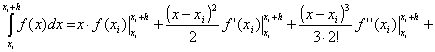 …=
…= =
=  . Получили формулу правых (или левых) прямоугольников и априорную оценку погрешности r на отдельном шаге интегрирования. Основной критерий, по которому судят о точности алгоритма – степень при величине шага в формуле априорной оценки погрешности.
. Получили формулу правых (или левых) прямоугольников и априорную оценку погрешности r на отдельном шаге интегрирования. Основной критерий, по которому судят о точности алгоритма – степень при величине шага в формуле априорной оценки погрешности. .
. .
. , то есть
, то есть  . Разложение функции в ряд Тейлора показывает, что в случае средних прямоугольников точность метода существенно выше:
. Разложение функции в ряд Тейлора показывает, что в случае средних прямоугольников точность метода существенно выше: .
. Метод трапеций.
Метод трапеций. .
.
 , а
, а 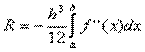 . Погрешность метода трапеций в два раза выше, чем у метода средних прямоугольников! Однако на практике найти среднее значение на элементарном интервале можно только у функций, заданных аналитически (а не таблично), поэтому использовать метод средних прямоугольников удается далеко не всегда. В силу разных знаков погрешности в формулах трапеций и средних прямоугольников истинное значение интеграла обычно лежит между двумя этими оценками.
. Погрешность метода трапеций в два раза выше, чем у метода средних прямоугольников! Однако на практике найти среднее значение на элементарном интервале можно только у функций, заданных аналитически (а не таблично), поэтому использовать метод средних прямоугольников удается далеко не всегда. В силу разных знаков погрешности в формулах трапеций и средних прямоугольников истинное значение интеграла обычно лежит между двумя этими оценками. которые проведем параболу, воспользовавшись уравнением Ньютона:
которые проведем параболу, воспользовавшись уравнением Ньютона: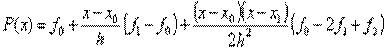 .
.

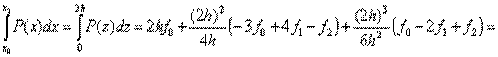
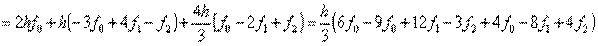 .
.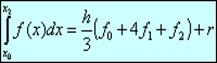

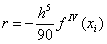 , а
, а  в предположении непрерывности четвертой производной подынтегральной функции.
в предположении непрерывности четвертой производной подынтегральной функции. .
.


