
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Погрешности вычислений на пэвмСодержание книги Поиск на нашем сайте
При проведении вычислений, в том числе на ПЭВМ всегда следует помнить, что результаты вычислений в подавляющем большинстве случаев являются приближенными, так как они содержат в себе целый ряд погрешностей. Мерой точности вычислений может служить либо абсолютная погрешность dx, представляющая собой разность между истинным значением искомой величины x и ее приближенным значением x'
либо относительная погрешность ddx, равная
При этом все источники погрешности вычислений можно подразделить на четыре группы. Первая группа погрешностей связана с формированием математической модели решаемой задачи. При математической постановке задачи оказываются неучтенными различные особенности изучаемого явления. Зачастую это определяется тем, что введение уточняющих членов приводит к значительным усложнениям математической модели, в том числе таким, при которых модель становится неприемлемой для вычислений. Эта группа получила название погрешностей математической модели. Вторая группа погрешностей определяется ошибками представления исходных данных для решения задачи. Исходные данные, полученные в результате измерений или каких либо вычислений, обязательно содержат погрешности, которые преобразуются в результат решения задачи. Погрешности, обусловленные ошибками исходных данных, получили название неустранимых погрешностей. Третья группа обусловлена погрешностями используемых методов решения задачи. Эти погрешности определяются как погрешности метода (методические погрешности). Для многих методов установлены строгие формулы оценки методической погрешности. Такие формулы имеются, например, для широко употребляемых численных методов вычисления интегралов, приближенных методов решения алгебраических и дифференциальных уравнений. Оценочные формулы отвечают на вопрос, каким должен быть минимальный объем работы для достижения заданной точности. Однако практическое применение таких формул требует большой предварительной работы по аналитическому исследованию математической модели задачи. Обычно исследователи, жертвуя строгостью при оценке погрешности метода, используют различные эмпирические приемы обеспечения требуемой точности решения, которые, как правило, себя оправдывают, но могут привести и к существенным ошибкам. Четвертую группу представляют погрешности округления, которые называются также вычислительными погрешностями. Эти погрешности обусловлены конечной длиной машинных слов для представления данных в ЭВМ. Общая погрешность вычислений на ЭВМ может быть определена как сумма указанных составляющих погрешностей. При вычислениях следует учитывать такое явление, как распространение ошибок. Ошибка, возникшая на входе вычислительного алгоритма или в определенном месте в ходе вычислений, распространяется дальше. Влияние ошибки на результат по мере выполнения последующих операций может увеличиваться или уменьшаться. Например, при вычитании почти равных чисел даже при достаточно маленьких ошибках представления этих чисел, относительная ошибка их разности может оказаться довольно большой. Эта большая ошибка будет распространяться дальше при выполнении всех последующих операций. На всех этапах решения задач на ЭВМ следует заботиться о том, чтобы гарантировать необходимую точность полученного результата. При этом следует придерживаться известных в литературе рекомендаций: · выражения, предназначенные для вычислений, следует преобразовать так, чтобы свести к минимуму число необходимых арифметических операций; · если нужно выполнить сложение-вычитание длинной последовательности чисел, сначала выполняются действия с наименьшими числами; · на промежуточных этапах следует избегать операций с почти равными числами.
|
||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 136; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.219.213 (0.009 с.) |

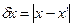 ,
,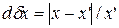 .
.


