
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
СИ с мультипликативной погрешностьюСодержание книги
Поиск на нашем сайте
Эта погрешность связана со случайными изменениями наклона функции преобразования. В этом случае сигнал на выходе СИ имеет вид: Найдём ширину полосы неопределённости в этом случае. При фиксированном значении выходного сигнала y, вследствие неопределенности D K значения K, это значение y реализуется при двух значениях х: Тогда ширина полосы неопределенности Будем считать, что Относительная мультипликативная погрешность остаётся постоянной при любых x, но такой идеальный случай практически не осуществим, т.к. нет СИ без аддитивных погрешностей.
В этом случае выходной сигнал имеет вид: Ширина полосы неопределенности В выше рассмотренных случаях речь шла об измерении малых величин и рассмотренные зависимости характерны для узкодиапазонных СИ. При больших х к оказывается, что погрешность может неограниченно расти, как и при
Измерение больших величин Что такое большие и малые измеряемые величины? Рассмотрим этот вопрос на примере измерения электрического сопротивления с помощью моста постоянного тока.
Условие равновесия моста в данном случае имеет вид Из (3): Очевидно Из (1) и (2) следует, что
Из (6) следует, что Учитывая, что резистор R 0 образцовый, его погрешностью Эта формула позволяет вычислить относительную погрешность измерений как больших, так и малых величин. Найдём вид полосы неопределённости. Поскольку, с учетом знаков абсолютной погрешности, сигнал на выходе нашего СИ, приведенный к входу, Поскольку абсолютная погрешность
При R x= R xмакс и R x= R xмин погрешность D R x=D R x max= R x, так что gRx=1 (или gRx=100%) и Ширина полосы неопределенности d определяется по формуле Т.к. при a <<1, где Значение Обобщим полученные результаты. Пусть в формуле (7)
Подставляя эти обозначения в формулу (7):
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 305; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.56.78 (0.008 с.) |

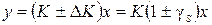 , где
, где 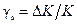 - относительная мультипликативная погрешность.
- относительная мультипликативная погрешность.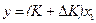 и
и 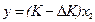 . Отсюда найдем
. Отсюда найдем 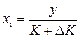 ,
,  .
. .
.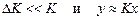 . Тогда
. Тогда 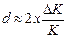 , и относительная мультипликативная погрешность
, и относительная мультипликативная погрешность 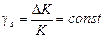 (см. рис.).
(см. рис.).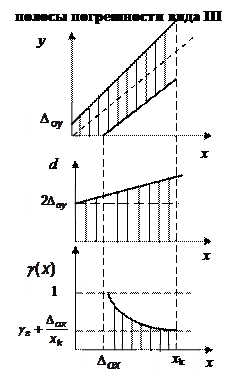
 СИ с аддитивной и мультипликативной погрешностями
СИ с аддитивной и мультипликативной погрешностями . Пусть, как и выше, относительная мультипликативная погрешность
. Пусть, как и выше, относительная мультипликативная погрешность 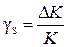 . Из рисунка видно, что границы полосы неопределенности задаются уравнениями
. Из рисунка видно, что границы полосы неопределенности задаются уравнениями 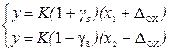
 . Относительная погрешность данного СИ
. Относительная погрешность данного СИ 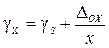 . Эту погрешность будем называть погрешностью вида III. Вид полос погрешности в данном случае имеет вид, показанный на втором рис.
. Эту погрешность будем называть погрешностью вида III. Вид полос погрешности в данном случае имеет вид, показанный на втором рис.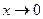 . Поэтому точное измерение больших величин оказывается такой же трудной задачей, как и измерение малых величин.
. Поэтому точное измерение больших величин оказывается такой же трудной задачей, как и измерение малых величин.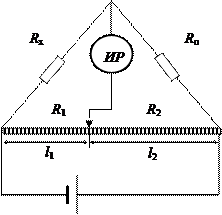 На рисунке ИР – индикатор равновесия, R 0 – образцовое сопротивление, R 1 и R 2 сопротивления плеч реохорда, l 1 и l 2 – длины плеч реохорда.
На рисунке ИР – индикатор равновесия, R 0 – образцовое сопротивление, R 1 и R 2 сопротивления плеч реохорда, l 1 и l 2 – длины плеч реохорда.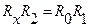 , откуда
, откуда 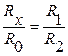 .(1). Очевидно, что
.(1). Очевидно, что 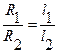 , (2), причем l 1+ l 2= L =const. (3). Из (1) и (2) следует, что
, (2), причем l 1+ l 2= L =const. (3). Из (1) и (2) следует, что  . Логарифмируя и дифференцируя это выражение, получим:
. Логарифмируя и дифференцируя это выражение, получим: 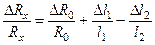 , где
, где 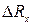 — погрешность оценки сопротивления R x,
— погрешность оценки сопротивления R x, 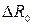 — погрешность образцового сопротивления R 0,
— погрешность образцового сопротивления R 0, 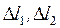 — погрешности измерения длины.
— погрешности измерения длины. , и (4), найдём:
, и (4), найдём: 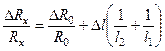 (5),
(5),  – относительная погрешность измерения.
– относительная погрешность измерения.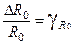 ,
,  . Можно записать (5) в виде:
. Можно записать (5) в виде: 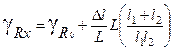 . Учитывая, что L = l 1+ l 2, после простого преобразования, получим
. Учитывая, что L = l 1+ l 2, после простого преобразования, получим 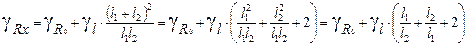 .
. , из предыдущего выражения, получим
, из предыдущего выражения, получим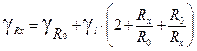 (6)
(6) как при R x®0, так и при R x®¥.
как при R x®0, так и при R x®¥. можно пренебречь. Тогда формула (6) запишется в виде
можно пренебречь. Тогда формула (6) запишется в виде 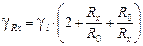 (7)
(7)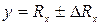 , вид полосы неопределенности определяется следующими соотношениями:
, вид полосы неопределенности определяется следующими соотношениями:  (8).
(8).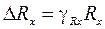 , из формулы(7), пренебрегая величиной
, из формулы(7), пренебрегая величиной 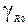 , имеем
, имеем 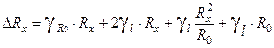 . (9). Учитывая (8), найдем максимальный и минимальный сигналы на выходе:
. (9). Учитывая (8), найдем максимальный и минимальный сигналы на выходе: 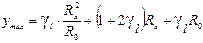 (10).
(10).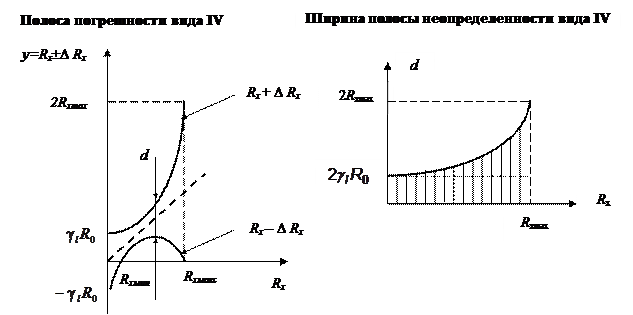 Функция
Функция  – парабола, ветви которой обращены вверх. В свою очередь,
– парабола, ветви которой обращены вверх. В свою очередь, 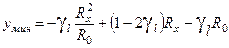 (11).Функция
(11).Функция 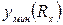 – парабола с ветвями, обращенными вниз. На графике зависимости
– парабола с ветвями, обращенными вниз. На графике зависимости 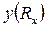 параметр d – ширина полосы неопределенности R xмакс и R xмин — максимальное и минимальное значения, которые еще могут быть измерены.
параметр d – ширина полосы неопределенности R xмакс и R xмин — максимальное и минимальное значения, которые еще могут быть измерены. .
.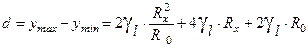 (12) Функция d (R x) – парабола. Обозначим в формуле (7)
(12) Функция d (R x) – парабола. Обозначим в формуле (7) 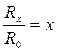 , тогда
, тогда  . Проведем анализ этой формулы. Сначала найдем минимум функции
. Проведем анализ этой формулы. Сначала найдем минимум функции 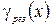 , взяв производную по х. Найдем, что при х =1
, взяв производную по х. Найдем, что при х =1 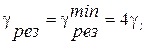 . Найдем максимально и минимально возможные значения х. Они находятся там, где
. Найдем максимально и минимально возможные значения х. Они находятся там, где 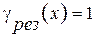 . Из этого равенства имеем
. Из этого равенства имеем  . Обычно
. Обычно  . Решая квадратное уравнение, получим
. Решая квадратное уравнение, получим 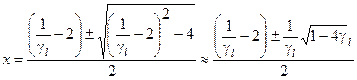 .
.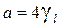 , выполняется соотношение
, выполняется соотношение  , получим:
, получим: 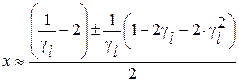 . Отсюда следует, что
. Отсюда следует, что 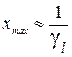 и
и  , где
, где 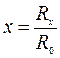 и
и 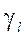 - погрешность реохорда. Отсюда легко найти минимальное и максимальное значения R x, которые можно измерить с погрешностью £100%. Таким образом, значения
- погрешность реохорда. Отсюда легко найти минимальное и максимальное значения R x, которые можно измерить с погрешностью £100%. Таким образом, значения 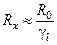 следует отнести к большим значениям, а значения
следует отнести к большим значениям, а значения 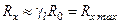 – к малым.
– к малым. – это нижний порог чувствительности данного СИ, значение
– это нижний порог чувствительности данного СИ, значение  – это верхний порог чувствительности СИ.
– это верхний порог чувствительности СИ. – любая величина, подлежащая измерению. Будим считать, что:
– любая величина, подлежащая измерению. Будим считать, что: — погрешность чувствительности,
— погрешность чувствительности,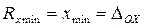 – нижний порог чувствительности,
– нижний порог чувствительности,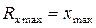 – верхний порог чувствительности,
– верхний порог чувствительности, – погрешность СИ.
– погрешность СИ.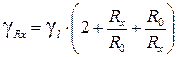 , получим универсальную формулу для расчета статических погрешностей СИ:
, получим универсальную формулу для расчета статических погрешностей СИ: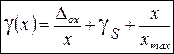 , (13), где
, (13), где  - абсолютная погрешность прибора (сдвиг нуля),
- абсолютная погрешность прибора (сдвиг нуля),  - погрешность чувствительности (погрешность наклона функции преобразования) или мультипликативная погрешность.
- погрешность чувствительности (погрешность наклона функции преобразования) или мультипликативная погрешность.


