
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интерполяционная формула ЛагранжаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
+является многочленом, интерполирующим сеточную функцию является многочленом, наименее отклоняющимся от нуля является многочленом наилучшего приближения для экспоненты является многочленом, интерполирующим логарифмическую функцию
41. Решение нелинейного уравнения определения знака производной записи итерационной формулы записи итерационной формулы +отделения корней исходного нелинейного уравнения; определение начальных условий для начала итерационного процесса. 42. По какой из нижеперечисленных итерационных формул осуществляется решение нелинейного уравнения вида
+ Какой из приведенных ниже подходов применяется при вычислении значений таблично-заданной функции в точках, расположенных ближе к началу таблицы? построение интерполяционной формулы Лагранжа; +построение I интерполяционной формулы Ньютона; построение II интерполяционной формулы Ньютона; построение аппроксимационного многочлена методом наименьших квадратов; построение экстраполяционного многочлена Адамса. 45. Приведите условие окончания итерационного процесса по методу простых итераций для решения нелинейного уравнения
+
одновременное выполнение условий
46. Норма матрицы вектор – строка; +число; вектор – столбец.
47. Норма 2 матрицы +30; 39; 28,6356. 48. Процесс построения значения корней системы с заданной точностью в виде предела последовательности некоторых векторов называется +итерационным; сходящимся; расходящимся.
49. Процесс Зейделя для линейной системы больше единицы; +меньше единицы; равна единице. 50. Процесс нахождения приближенных значений корней уравнения разбивается на построение графика и уточнение корней до заданной степени точности; +отделение корней и уточнение корней до заданной степени точности; уточнение корней до заданной степени точности и определение
Интерполяционным многочленом называется многочлен, +а) значения которого в узлах интерполяции равны значению табличной функции в этих узлах;
параболического вида. 52. Конечные табличные разности используются в интерполяционной формуле Гаусса для равноотстоящих узлов интерполяции; Эйткина для равноотстоящих узлов интерполяции; +Ньютона для равноотстоящих узлов интерполяции; Лагранжа для равноотстоящих узлов интерполяции.
Максимальная сумма модулей элементов матрицы по строкам есть норма 2; норма 3; +норма 1. 54. Норма 3 матрицы 30; 39; +28,6356.
55. Итерационный процесс построения приближений по формуле методом Зейделя; методом Ньютона; +методом итерации. 56. Процесс Зейделя для линейной системы +какая - ни будь из норм матрицы и только если норма 1 матрицы и только если норма 1 матрицы 57. Число отрицательных корней уравнения +а) перемен знака в последовательности коэффициентов постоянств знака в последовательности коэффициентов постоянств знака в последовательности коэффициентов
58. Верхняя граница положительных корней уравнения
+
|
|||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 1466; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.101.224 (0.011 с.) |

 начинается с:
начинается с: на отрезке
на отрезке  ;
; и проверки условия сходимости итерационного процесса на отрезке
и проверки условия сходимости итерационного процесса на отрезке  , где значение постоянной
, где значение постоянной  определяется из условий сходимости итерационного процесса;
определяется из условий сходимости итерационного процесса; упрощенным методом Ньютона?
упрощенным методом Ньютона? ;
; ;
; ;
;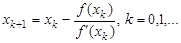 ;
;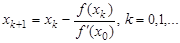 .
. .
. ;
; ;
; ;
; .
.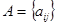 - это
- это равна
равна сходится
сходится
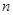 -й степени;
-й степени; называется
называется равно числу
равно числу или на четное число меньше;
или на четное число меньше; или на четное число меньше.
или на четное число меньше.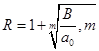 - номер первого отрицательного коэффициента,
- номер первого отрицательного коэффициента, 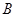 - наибольшая из абсолютных величин отрицательных коэффициентов
- наибольшая из абсолютных величин отрицательных коэффициентов  ;
; ;
; , при котором
, при котором 


