Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Простейшие квадрат ф-лы Н-Кот. и оценка их погрешности.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пример 1. Положим
и получаем квадратурн. ф-лу Квадратурную формулу (1) наз-ют квадратурной формулой ср. прямоугольников, т.к. здесь интеграл приближается площадью (квадратурой) прямоугольника с шириной, равной длине отрезка интегрирования, и высотой, равной значению подынтегральной функции в середине отрезка интегрирования. Используя разложение подынтегральной функции в ряд Тэйлора в точке
Отсюда для погрешности квадратурной формулы получаем выражение
и получаем квадратурную формулу
Квадратурную формулу (3) называют квадратурной формулой трапеций, потому что здесь интеграл приближается площадью трапеции с высотой, равной длине отрезка интегрирования, и основаниями, равными значениям подынтегральной функции на концах отрезка интегрирования. Подынтегральную функцию выразим через ее интерполяционный многочлен по узлам
Пример 3. Положим
и получаем квадратурную формулу
Квадратурную формулу (5) называют квадратурной формулой парабол или квадратурной формулой Симпсона. Здесь интеграл от функции приближается интегралом от интерполяционного многочлена второй степени (параболы) с узлами
где
Проводя три раза интегрирование и используя при этом теорему о среднем, имеем
Составные квадратурные формулы средних прямоугольников, трапеций, парабол и оценка их погрешности Как видно из выражения (2) предыдущего параграфа, погрешность квадратурной формулы средних прямоугольников есть величина третьего порядка относительно длины
Полученную квадратурную формулу называют составной квадратурной формулой средних прямоугольников. Для погрешности составной квадратурной формулы средних прямоугольников получаем
Учитывая, что Используя квадратурную формулу трапеций при интегрирования по частичным отрезкам
Полученную квадратурную ф-лу: называют составной квадратурной формулой трапеций. Для погрешности составной квадратурной формулы трапеций получаем
Т.к. Применим теперь при четном n к интегрированию на частичных отрезках Найдем выражение для погрешности расчетной формулы (3).
Как видно из выражений, полученных для остаточных членов Квадратурные формулы Гаусса Опр. Говорят, что квадратурная формула
имеет алгебраическую степень точности m, если она является точной для любого многочлена степени Квадратурные формулы наивысшей алгебраической степени точности называют квадратурными формулами Гаусса (при этом n считается фиксированным). Квадратурное правило имеет алгебраическую степень точности не ниже n тогда и только тогда, когда оно является интерполяционным. Следовательно, коэффициенты квадратурных правил Гаусса определяются формулой
Таким образом, остается найти оптимальный набор узлов, при котором интерполяционная квадратурная формула будет иметь наивысшую алгебраическую степень точности. Последняя, как будет доказано, равна Лемма 1. Если квадратурное правило (1) имеет алгебраическую степень точности Д-во. Так как квадратурное правило (1) является точным для любого многочлена степени Из леммы 1 следует, что для построения квадратурного правила алгебраической степени точности Лемма 2. Если Д-во. Для искомого приведенного многочлена относительно неизвестных коэффициентов Пусть Лемма 3. Если узлами интерполяционной квадратурной формулы (1) являются нули ортогонального многочлена Д-во. Пусть
Теорема. Если Д-во. Существование квадратурного правила (1) алгебр-кой степени точности
19. Квадр-ные формулы Гаусса с постоянной весовой ф-ей. Рассмотрим интеграл Обозначим
Продолжая процесс интегрирования по частям получим
Таким образом, многочлен получим выражение Ортогональные многочлены, определяемые формулой (3) называют многочленами Лежандра. В случае выбора константы по правилу При этом получается квадрат нормы По формуле(3) находим
При При Формула для вычисления коэффициентов квадратурной формулы (2) может быть преобразована к виду При Метод наименьших квадратов. Пусть ф-ия f(x) задана табл. yi=f(xi); i=0,…n. Надо эту ф-ию приблизить ф-ей вида φ(x, a0,...,am). Знач-я неизвест-х парам-ов aj;j=0,...m надо выбрать т.ч. сумма кв-ов отклонений
Когда ф-ия φ линейно зависит от параметров:
Определитель Теорема. Если последов-ть непрерывных ф-ций Доказательство. Противное: последов-сть ф-ий явл. сис-мой Чебышева на отр-е, но
При m=n единственным решение – интерполяц-ый обобщенный многочлен φ(x); при этом min сумма квадратов отклонений: Ф=0. Сис-ма ф-ий
|
||||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 636; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.57.57 (0.008 с.) |

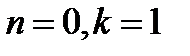 . В этом случае
. В этом случае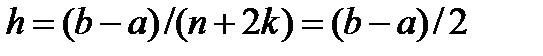 ;
; 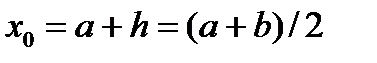 ;
;
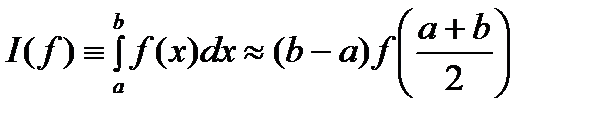 (1)
(1) , имеем
, имеем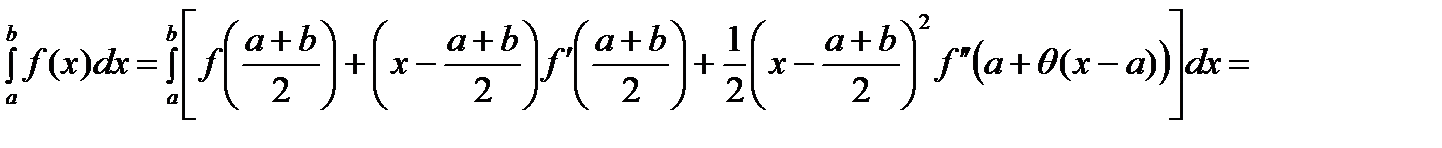
 .
.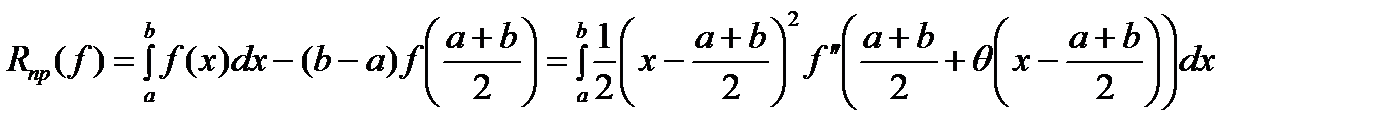 Применение теоремы о среднем дает (2):
Применение теоремы о среднем дает (2):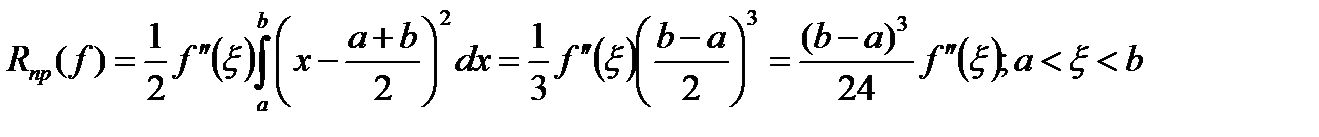 Пример 2. Положим
Пример 2. Положим  . В этом случае
. В этом случае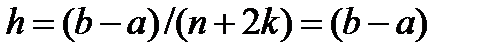 ;
;  ;
; 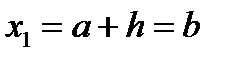 ;
;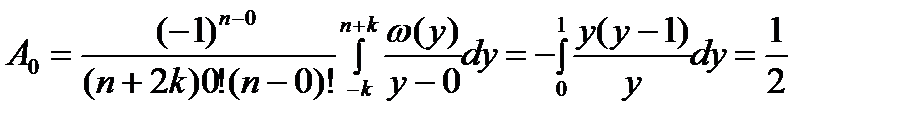 ;
;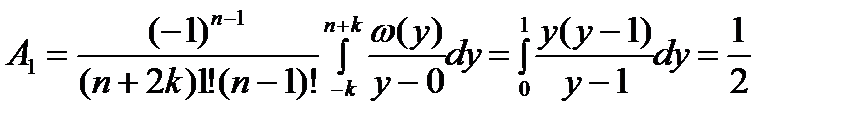 .
.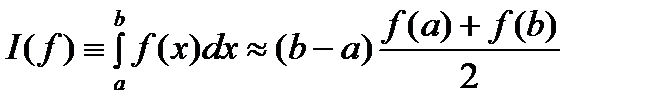 . (3)
. (3)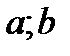 и остаточный член интерполяционного многочлена. Тогда получим
и остаточный член интерполяционного многочлена. Тогда получим 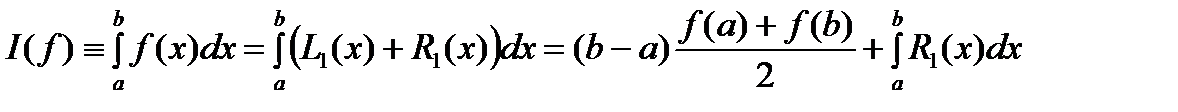 Отсюда для погрешности квадрат. ф-лы трапеций получ. выр.
Отсюда для погрешности квадрат. ф-лы трапеций получ. выр.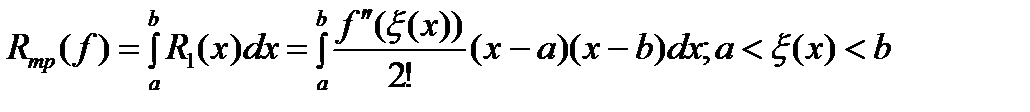 Применяя теорему о среднем, имеем
Применяя теорему о среднем, имеем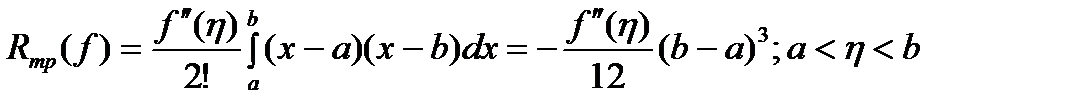 . (4)
. (4)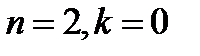 . В этом случае
. В этом случае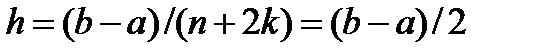 ;
; 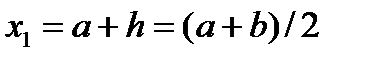 ;
; 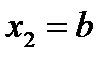 ;
;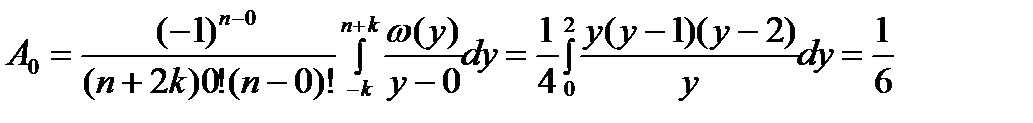 ;
;  ;
;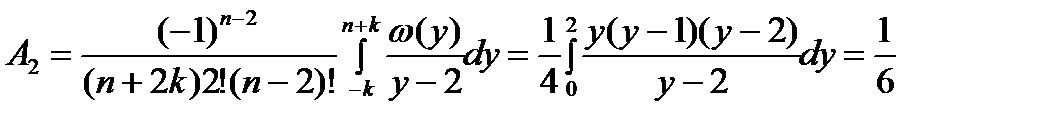 .
.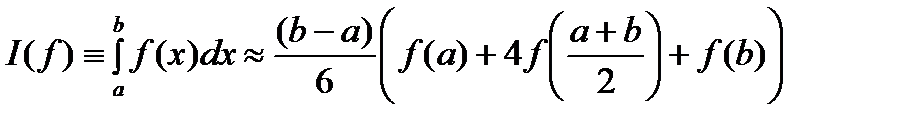 . (5)
. (5) . Погрешность квадратурной формулы (5) запишем в виде
. Погрешность квадратурной формулы (5) запишем в виде , (6)
, (6)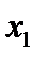 будем считать константой, а h – переменной. Очевидно,
будем считать константой, а h – переменной. Очевидно, 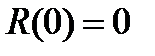 .Выполним дифференцирование равенства (6) по h:
.Выполним дифференцирование равенства (6) по h: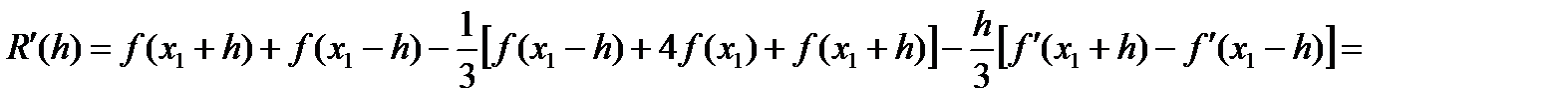
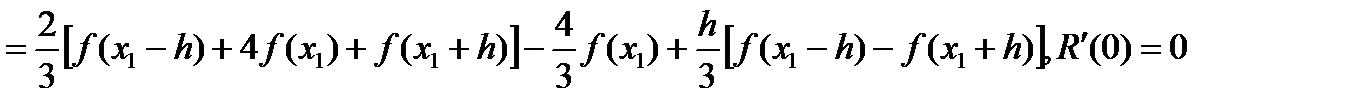 Проводя дифференцирование еще два раза и используя формулу конечных приращений, получим
Проводя дифференцирование еще два раза и используя формулу конечных приращений, получим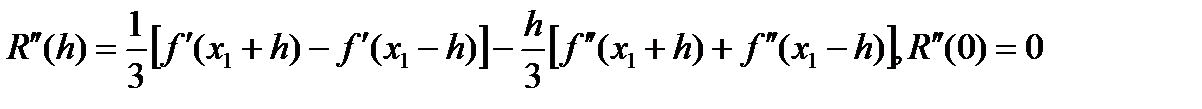 ,
,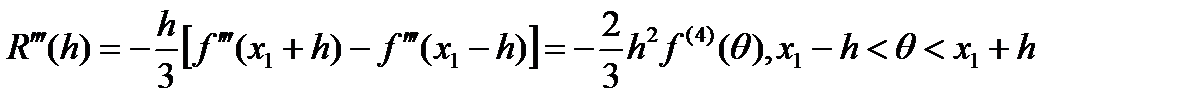 . (7)
. (7)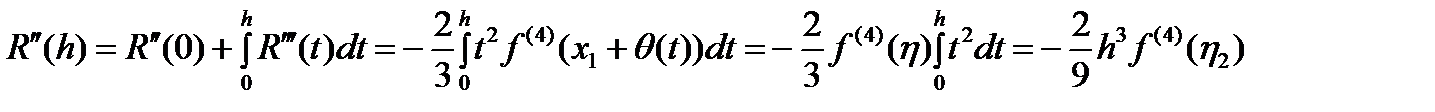 ,
, 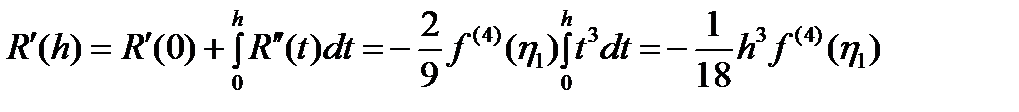 ,
, 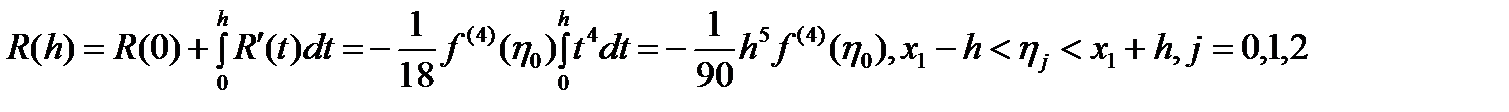 Полученное выражение для остаточного члена перепишем в виде
Полученное выражение для остаточного члена перепишем в виде 
 отрезка интегрирования. Таким образом, при большой длине отрезка интегрирования погрешность указанной квадратурной формулы также может быть большой.На отрезке
отрезка интегрирования. Таким образом, при большой длине отрезка интегрирования погрешность указанной квадратурной формулы также может быть большой.На отрезке 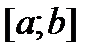 введем равномерную сетку
введем равномерную сетку 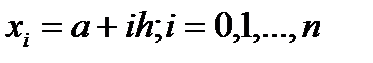 с шагом
с шагом 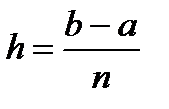 . Интеграл по всему отрезку равен сумме интегралов по частичным отрезкам. Применяя квадратурную формулу средних прямоугольников в случае четного
. Интеграл по всему отрезку равен сумме интегралов по частичным отрезкам. Применяя квадратурную формулу средних прямоугольников в случае четного 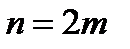 к частичным отрезкам
к частичным отрезкам  , имеем
, имеем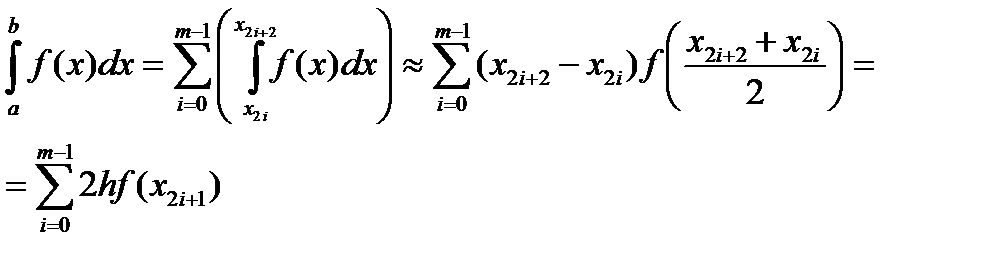 .
.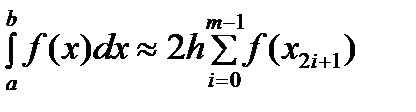 (1)
(1)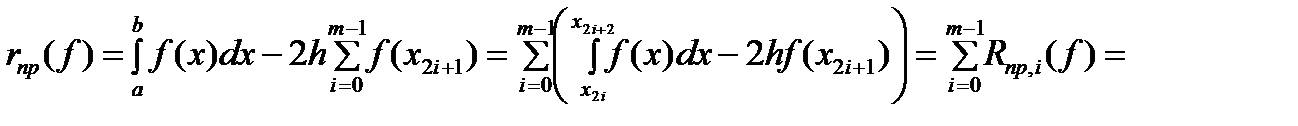
 .
. и
и  , отсюда следует искомое равенство
, отсюда следует искомое равенство 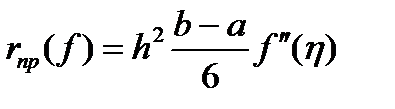 . (2)
. (2) , имеем
, имеем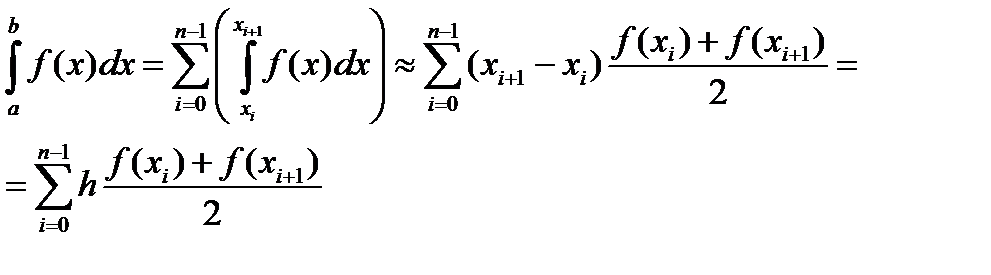 .
.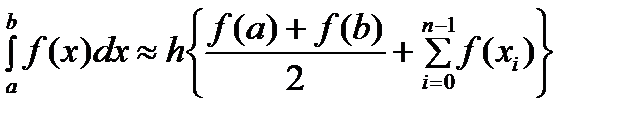 (3)
(3)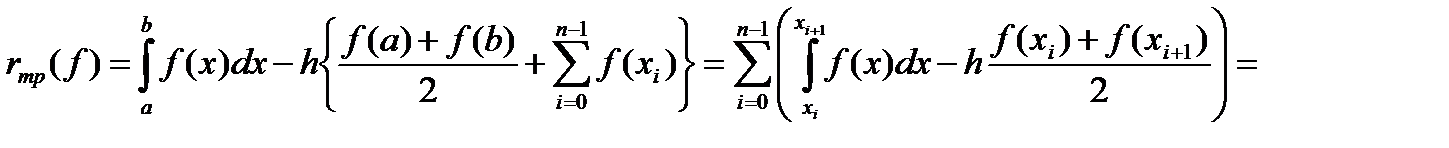
 .
.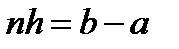 и
и 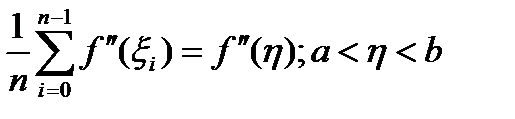 , то искомая пог-ть представляется в виде
, то искомая пог-ть представляется в виде 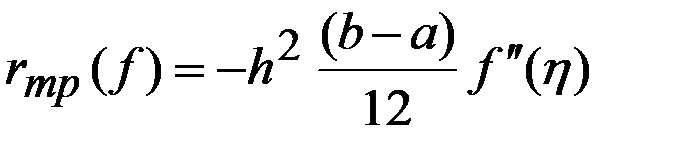 . (4)
. (4)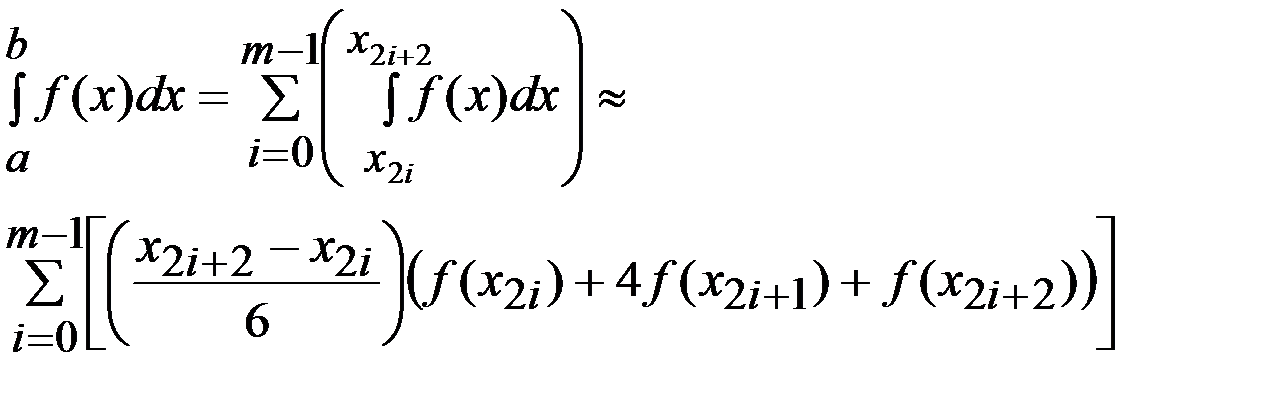 . Полученную квадратурную формулу
. Полученную квадратурную формулу 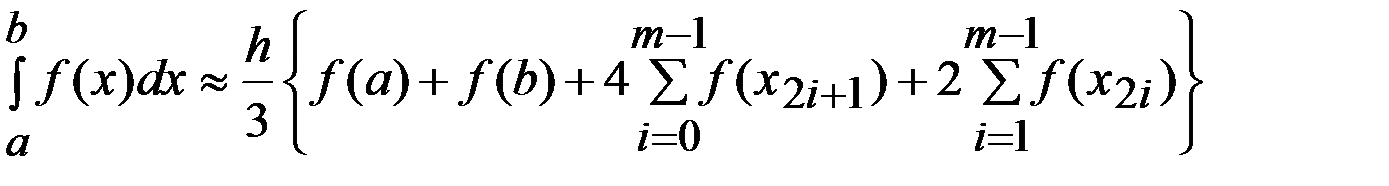 (5) наз-ют составной квадратурной формулой парабол (Симпсона).
(5) наз-ют составной квадратурной формулой парабол (Симпсона).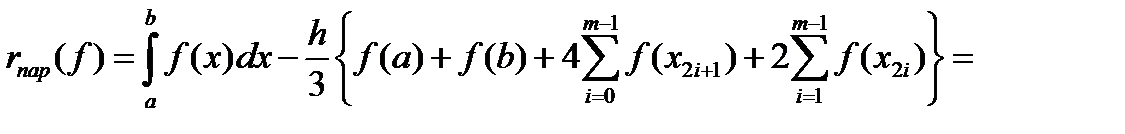
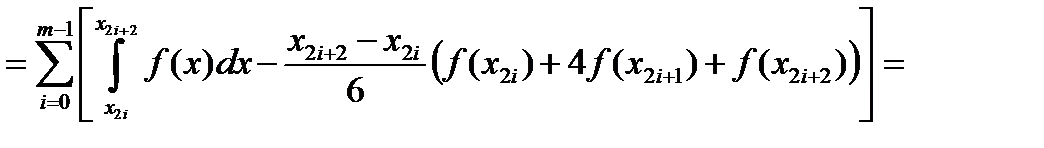
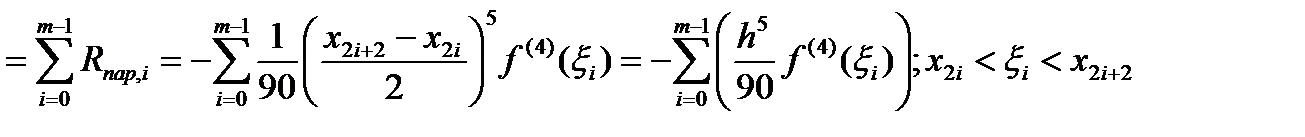 Учитывая, что
Учитывая, что 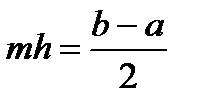 и
и  , отсюда следует искомое равенство
, отсюда следует искомое равенство 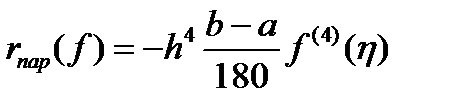 .(6)
.(6)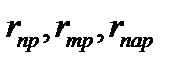 , погрешность составных квадратурных формул можно сделать достаточно малой за счет выбора меньшего шага сетки h. При этом подынтегральная функция должна быть достаточно гладкой на отрезке
, погрешность составных квадратурных формул можно сделать достаточно малой за счет выбора меньшего шага сетки h. При этом подынтегральная функция должна быть достаточно гладкой на отрезке 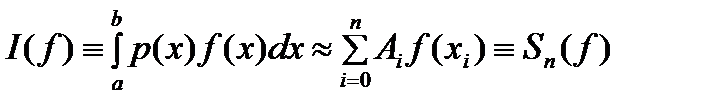 (1)
(1)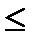 m и существует многочлен степени
m и существует многочлен степени 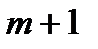 , для которого квадратурная формула не является точной.
, для которого квадратурная формула не является точной.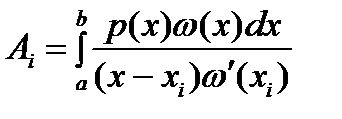 . (2)
. (2) .
.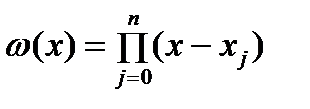 степени
степени 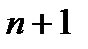 ортогонален с весом
ортогонален с весом 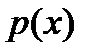 на отрезке
на отрезке 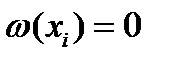 ,то при
,то при 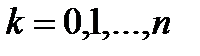 имеем
имеем  , что док-ет лемму.
, что док-ет лемму. почти всюду на
почти всюду на 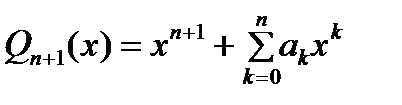 степени
степени 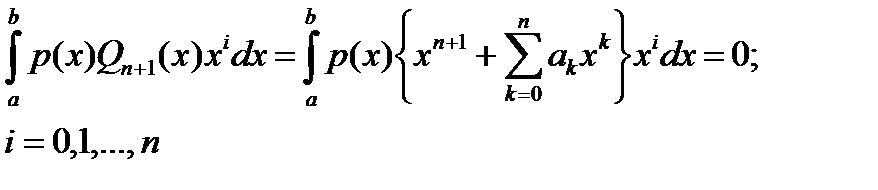 (3)
(3)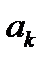 . Системе (3) соответствует однородная система
. Системе (3) соответствует однородная система 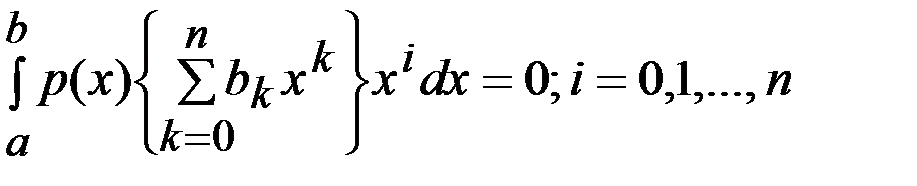 (4).Уравнения системы (4) умножим на соответствующие коэффициенты
(4).Уравнения системы (4) умножим на соответствующие коэффициенты 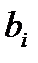 и сложим. Из полученного при этом выражения
и сложим. Из полученного при этом выражения  и условия леммы
и условия леммы 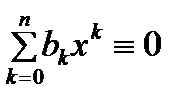 , т.е.
, т.е. 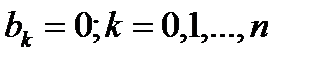 . Поскольку однородная система (4) имеет только тривиальное решение, то соответствующая неоднородная система (3) имеет единственное решение.
. Поскольку однородная система (4) имеет только тривиальное решение, то соответствующая неоднородная система (3) имеет единственное решение.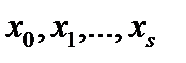 - корни нечетной кратности многочлена
- корни нечетной кратности многочлена 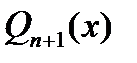 , лежащие на отрезке
, лежащие на отрезке 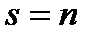 . Допустим противное:
. Допустим противное:  . Тогда, в силу ортогональности, выполняется
. Тогда, в силу ортогональности, выполняется 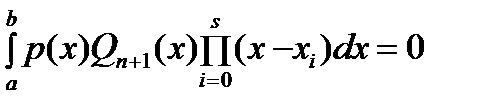 . С другой стороны, так как
. С другой стороны, так как 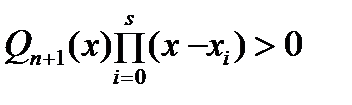 почти всюду на
почти всюду на  . Полученное противоречие доказывает, что
. Полученное противоречие доказывает, что  , то квадратурная формула точна для любого мн-на степени
, то квадратурная формула точна для любого мн-на степени 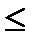
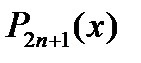 - произвольный многочлен степени
- произвольный многочлен степени  ,где
,где 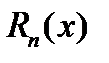 и
и  -многочлены степени n. Имеем
-многочлены степени n. Имеем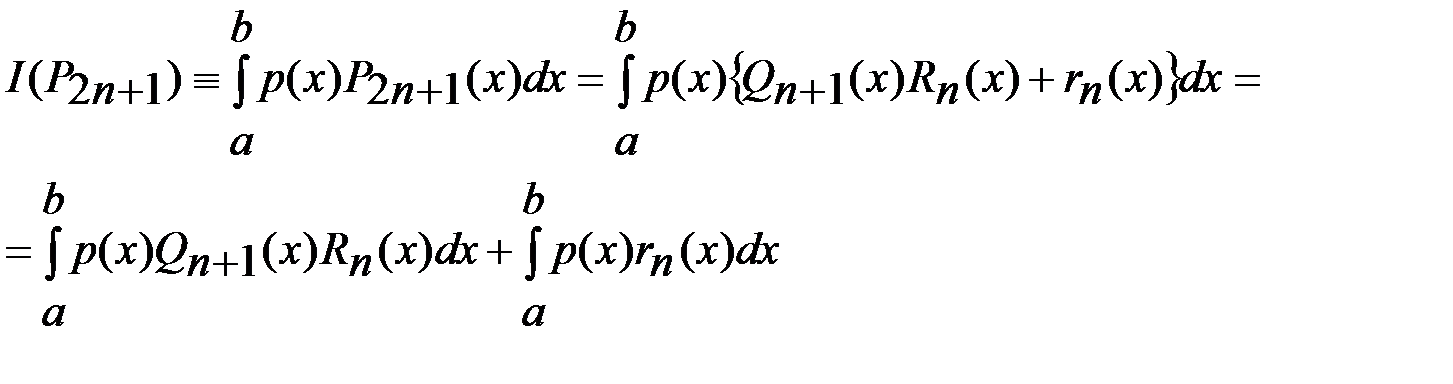 Здесь
Здесь  в силу ортогональности
в силу ортогональности 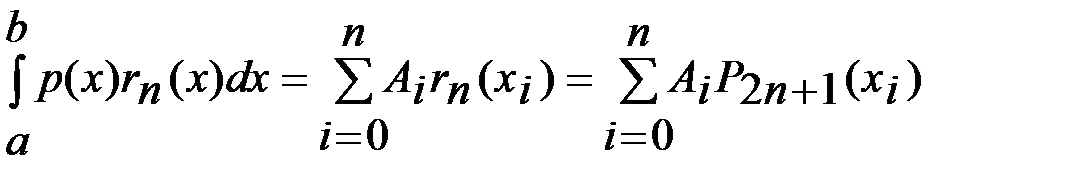 . Лемма доказана.
. Лемма доказана. . Для многочлена
. Для многочлена 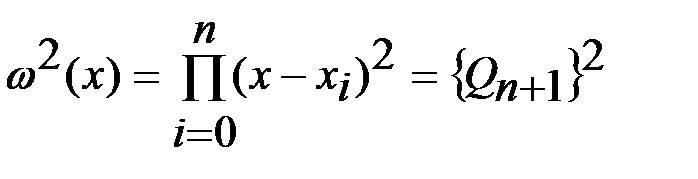 степени
степени  и значение квадратурной суммы
и значение квадратурной суммы .Т-ма док-на.
.Т-ма док-на.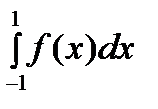 , (1) где
, (1) где  - достаточно гладкая функция. Любой конечный отрезок интегрирования
- достаточно гладкая функция. Любой конечный отрезок интегрирования  . Поскольку в данном случае весовая функция
. Поскольку в данном случае весовая функция 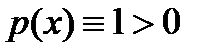 , то квадратурное правило наивысшей алгебраической степени точности
, то квадратурное правило наивысшей алгебраической степени точности  (2)существует. Его узлами явл-ся корни мн-на
(2)существует. Его узлами явл-ся корни мн-на  , ортогонального мн-нам меньшей степени с весом 1 на отрезке [-1;1].
, ортогонального мн-нам меньшей степени с весом 1 на отрезке [-1;1].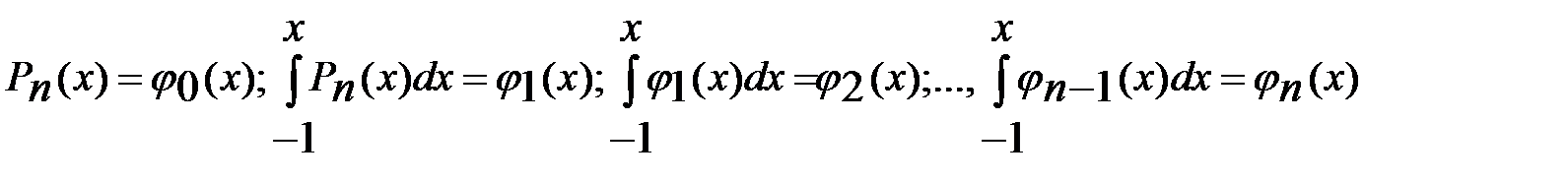 . Очевидно,
. Очевидно, 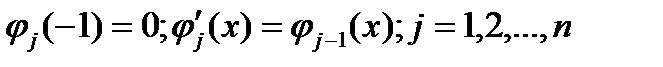 и
и  . Возьмем произвольный многочлен
. Возьмем произвольный многочлен 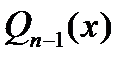 степени
степени 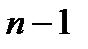 . Используя условия ортогональности и проводя интегрирование по частям, получим
. Используя условия ортогональности и проводя интегрирование по частям, получим 
 .
.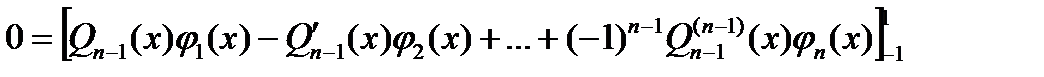 Отсюда для
Отсюда для 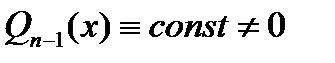 , следует, что
, следует, что  . Используя произвольность многочлена
. Используя произвольность многочлена  .
. степени
степени 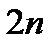 , производные которого определяются формулой
, производные которого определяются формулой 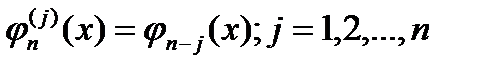 имеет корни
имеет корни 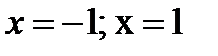 , каждый кратности n. Следовательно, этот многочлен представляется в виде
, каждый кратности n. Следовательно, этот многочлен представляется в виде 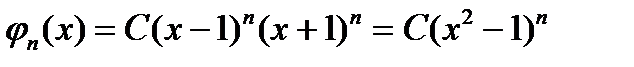 . Для искомого ортогонального многочлена в результате
. Для искомого ортогонального многочлена в результате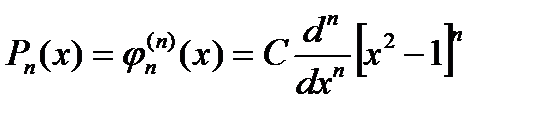 .(3)
.(3)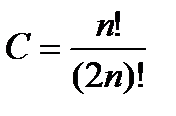 будут получаться приведенные многочлены. В практике вычислений для многочленов Лежандра используется формула Родрига
будут получаться приведенные многочлены. В практике вычислений для многочленов Лежандра используется формула Родрига 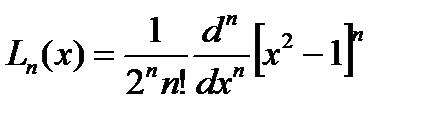 .(4)
.(4) и рекуррентная формула
и рекуррентная формула 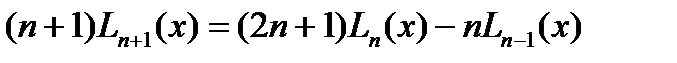 .(5)
.(5)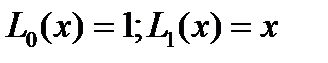 . По формуле (4) находим
. По формуле (4) находим  . Отсюда определяем последовательно
. Отсюда определяем последовательно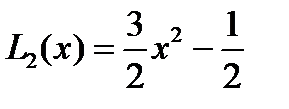 и
и  . Построим несколько квадратурных формул Гаусса вида (2).
. Построим несколько квадратурных формул Гаусса вида (2).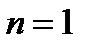 из уравнения
из уравнения 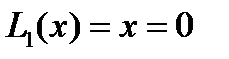 получаем один корень
получаем один корень 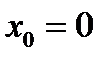 ,
, 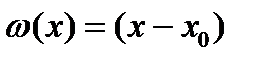 и один коэффициент
и один коэффициент  . Приходим к квадратурной формуле
. Приходим к квадратурной формуле 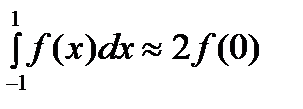 , имеющей наивысшую алгебраическую степень точности 1.
, имеющей наивысшую алгебраическую степень точности 1.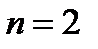 из уравнения
из уравнения  получаем два корня
получаем два корня 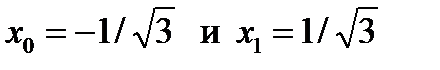 ,
,  и два коэффициента
и два коэффициента 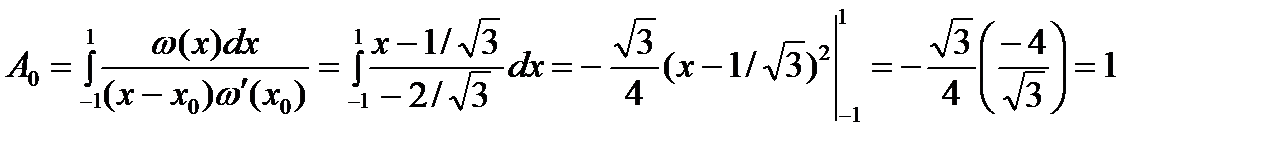 и
и 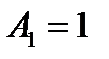 . Приходим к квадратурной формуле
. Приходим к квадратурной формуле 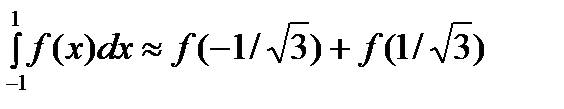 , имеющей наивысшую алгебр-скую степень точности 3.
, имеющей наивысшую алгебр-скую степень точности 3.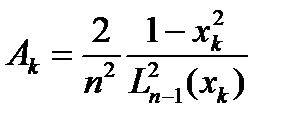 (6)
(6)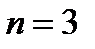 из уравнения
из уравнения  получаем три корня
получаем три корня 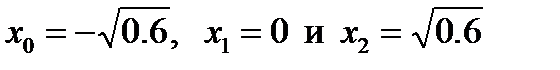 и три коэффициента
и три коэффициента 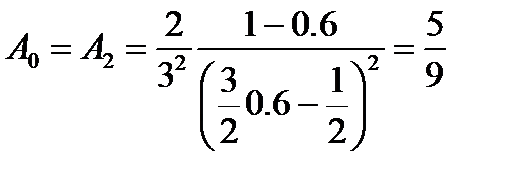 и
и  . Приходим к квадратурной формуле
. Приходим к квадратурной формуле 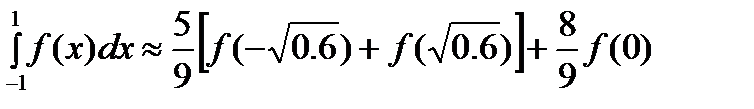 , имеющей наивысшую алгебраическую степень точности 5.
, имеющей наивысшую алгебраическую степень точности 5.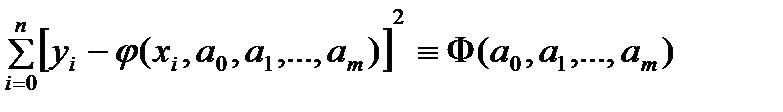 (1) ф-ии f от ф-ии φ по всем табл-ым узлам xi была мин-ой. Е. ф-ия φ явл. достаточно гладкой, то искомые зн. параметров м.б. найдены из условий Ферма
(1) ф-ии f от ф-ии φ по всем табл-ым узлам xi была мин-ой. Е. ф-ия φ явл. достаточно гладкой, то искомые зн. параметров м.б. найдены из условий Ферма 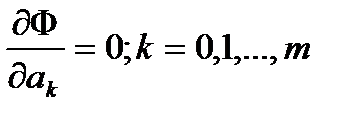 . (2)
. (2) , с-ма (2) будет линейной
, с-ма (2) будет линейной  . После простых преобразований с-ма:
. После простых преобразований с-ма: .(3)
.(3) с-мы - определитель Грама с элементами Akj, равными скалярным произвед-ям
с-мы - определитель Грама с элементами Akj, равными скалярным произвед-ям  .
.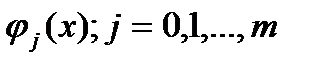 явл. сис-мой Чебышева на [a;b], то определитель с-мы (3) ≠ 0 при любых наборах попарно неравных узлов
явл. сис-мой Чебышева на [a;b], то определитель с-мы (3) ≠ 0 при любых наборах попарно неравных узлов 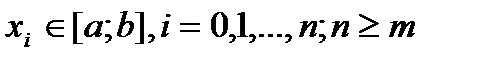 .
.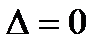 при некот-ом наборе попарно неравных узлов. Тогда столбцы определителя будут линейно зависимыми
при некот-ом наборе попарно неравных узлов. Тогда столбцы определителя будут линейно зависимыми  . =>
. =>  . Умножая последние равенства на соответствующие ck и проводя суммирование по k, получим
. Умножая последние равенства на соответствующие ck и проводя суммирование по k, получим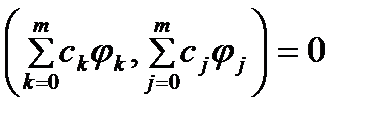 , откуда
, откуда  . Т. о., нетривиальный обобщенный многочлен
. Т. о., нетривиальный обобщенный многочлен 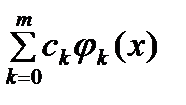 обращается в 0 на отрезке не менее чем в n+1 -й точке, что > m. Полученное противоречие доказывает теорему.
обращается в 0 на отрезке не менее чем в n+1 -й точке, что > m. Полученное противоречие доказывает теорему.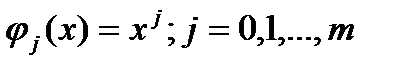 явл. сис-мой Чебышева на любом отр., поэтому наилучшее приближение табличной ф-ии yi=f(xi) алгебраическим многочленом
явл. сис-мой Чебышева на любом отр., поэтому наилучшее приближение табличной ф-ии yi=f(xi) алгебраическим многочленом 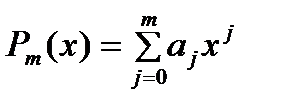 степени m<=n по методу наименьших квадратов сущ-ет, явл. единственным и коэффиценты многочлена м.б. найдены из линейной алгебраической системы
степени m<=n по методу наименьших квадратов сущ-ет, явл. единственным и коэффиценты многочлена м.б. найдены из линейной алгебраической системы 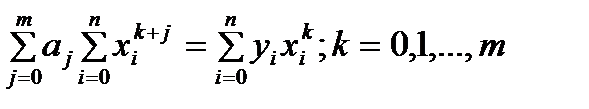 . При m=2 система:
. При m=2 система: