
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Разложение квадратного трехчлена.
Когда мы решали квадратные уравнения (вспомните прошлые уроки), то слева у нас стояло выражение следующего вида: ax 2 + bx + c. Это выражение называется квадратным трехчленом. Давайте обсудим, как разложить на множители выражения такого типа. Пусть x 1 и x 2 ― корни квадратного уравнения ax 2 + bx + c = 0 (уже умеем его решать!), тогда имеет место равенство: ax 2 + bx + c = a (x – x 1)(x – x 2). Таким образом, чтобы разложить квадратный трехчлен на множители, надо найти корни квадратного уравнения, в левой части которого стоит исходное выражение. Пример: Разложить на множители выражение x 2 + 3 x – 4. Заметим, что это квадратный трехчлен, поэтому решаем квадратное уравнение: x 2 + 3 x – 4 = 0. По теореме Виета получаем: x 1 = 1; x 2 = –4. Таким образом, исходное выражение принимает вид: x 2 + 3 x – 4 = 1(x – 1)(x + 4) = (x – 1)(x + 4). Разложение с помощью формул сокращенного умножения. Вспомним, что это за формулы, с прошлых уроков: a 2 – b 2 = (a – b)(a + b) ― разность квадратов. Эта формула позволяет разложить разность квадратов выражений на множители. Пример 1: 25 x 2 – 9 y 2 = (5 x)2 – (3 y)2 = (5 x – 3 y)(5 x + 3 y). Следующие две формулы позволяют раскладывать на множители трехчлены соответствующего вида (рассмотрим их на примерах): a 2 + 2 ab + b 2 = (a + b)2 ― квадрат суммы; a 2 – 2 ab + b 2 = (a – b)2 ― квадрат разности. Пример 2: Применим формулу квадрата суммы: 16 a 2 + 56 ab + 49 b 2 = (4 a)2 + 2 ∙ 4 a ∙ 7 b + (7 b)2 = (4 a + 7 b)2. Пример 3: Применим формулу квадрата разности: 4 x 2 – 4 x + 1 = (2 x)2 – 2 ∙ 2 x ∙ 1 + 12 = (2 x – 1)2. Метод группировки. Рассмотрим разложение многочлена на множители методом группировки на конкретном примере: 35 a 2 + 7 a 2 b 2 + 5 b + b 3; сгруппируем слагаемые скобками следующим образом: (35 a 2 + 7 a 2 b 2) + (5 b + b 3); вынесем за скобки общий множитель первой, а затем и второй группы 7 a 2(5 + b 2) + b (5 + b 2); у нас получилось выражение из двух слагаемых, в каждом из которых присутствует общий множитель (5 + b 2), который мы вынесем за скобку (7 a 2 + b)(5 + b 2). Таким образом, получаем: 35 a 2 + 7 a 2 b 2 + 5 b + b 3 = (7 a 2 + b)(5 + b 2). Итак, мы познакомились с понятием многочлена и рассмотрели важную задачу, которая с ними возникает ― разложение многочлена на множители. Эта задача может быть решена различными методами: вынесением за скобку повторяющегося выражения, разложением квадратного трехчлена, применением формул сокращенного умножения и, конечно, важным методом группировки.
Рациональные уравнения Решить любое уравнение ― это значит найти такое значение переменной x, которое превращает исходное уравнение в равенство. Например, для уравнения 2 x = 10, при x = 5, получаем 2 ∙ 5 = 10 или 2 ∙ 5 = 10 ― верное равенство. Основные свойства в любых уравнениях: · Любое слагаемое в уравнении можно перенести из одной части уравнения в другую, изменив его знак на противоположный. Пример 1 (числовое уравнение): 9 = 8 + 1; 9 – 1 = 8; 8 = 8. Пример 2 (буквенное уравнение): a = b + c; a – c = b; где a, b, c ― какие-то числа или переменные. · Можно умножать и делить левую и правую части уравнения на одно и то же ненулевое число или выражение (при умножении на ноль уравнение теряет смысл; а при делении вспоминаем важное правило в математике ― на ноль делить нельзя). Пример 1 (численное уравнение): 4 = 4 | ∙ 2; 4 ∙ 2 = 4 ∙ 2; 8 = 8; или 4 = 4 |: 2; 4: 2 = 4: 2; 2 = 2. Пример 2 (буквенное уравнение ― деление): 4 a = 4 |: 4; 4 a: 4 = 4: 4; a = 1. Рассмотрим далее основные виды уравнений и примеры их решения. Линейное уравнение Линейное уравнение, после всех преобразований, записывается в виде ax = b. И для решения достаточно поделить все уравнение на a и получить ответ. Рассмотрим это на примерах. Пример 1: Решить уравнение: 3(x – 5) – 5 = – x. Раскроем скобки и приведем уравнения к общему виду, используя свойства уравнений: 3 x – 15 – 5 + x = 0; 4 x = 20 |: 4; x = 5. Ответ: 5. Пример 2: Решить уравнение: Замечание: обратим внимание, что в знаменателях всех дробей стоит какое-то число, а не выражение, содержащее переменную x, поэтому уравнение линейное. Применим свойство уравнений, т. е. надо умножить это уравнение на такое число, чтобы избавиться от дробей. Это число 6, такое число называется общим знаменателем. Получим уравнение:
Сделаем вычисление и получаем:
2 x – 6 = 5 ∙ 3; 2 x = 15 + 6; 2 x = 21; x = 10,5. Ответ: 10,5. Квадратное уравнение Рассмотрим квадратное уравнение в общем виде: ax 2 + bx + c = 0, где a, b, c ― какие-то числа.
Для решения данного уравнения рассматривают формулы: D = b 2 – 4 ac; x 1 = x 2 = где D ― дискриминант квадратного уравнения, x 1, x 2 ― корни квадратного уравнения. Пример 1: Решить уравнение: x 2 = – x + 6. Преобразуем уравнение, используя свойства, приведём к общему виду и найдем, чему равны a, b, c. x 2 + x – 6 = 0; a = 1; b = 1; c = –6; D = b 2 – 4 ac = 12 – 4 ∙ 1 ∙ (–6) = 1 + 4 ∙ 6 = 1 + 24 = 25. x 1 = x 2 = Ответ: –3, 2. В некоторых случаях (например, когда a = 1) квадратное уравнение легче и быстрее решить, используя теорему Виета: пусть x 1, x 2 корни квадратного уравнения ax 2 + bx + c = 0, тогда выполнены следующие равенства: x 1 + x 2 = – x 1 ∙ x 2 = Пример 2: Решить уравнение: x 2 – 5 x + 6 = 0. По теореме Виета: сумма корней равна 5, а произведение равно 6. Тогда корнями являются числа 2 и 3. Ответ: 2; 3.
|
||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 863; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.213.214 (0.01 с.) |
 – 1 =
– 1 =  .
. ;
; ;
; =
=  =
=  = 2.
= 2. =
= 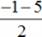 =
=  = –3.
= –3. при a = 1 → x 1 + x 2 = – b;
при a = 1 → x 1 + x 2 = – b; при a = 1 → x 1 ∙ x 2 = c.
при a = 1 → x 1 ∙ x 2 = c.


