
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод Рунге-Кутта решения задачи Коши. Построение методов Р-К второго порядка точности.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим задачу Коши
…………….. (
(3). Алгоритм задается так: 1)полагаем 2) вычисляем функции
…
3) вычисляем 4) вычисляем Рассмотрим схему построения методов Рунге – Кутта в случае q=1. В этом случае метод явл. 2 порядка точности, при q=1 исп. 4 параметра: Расчетная ф-ла примет вид Обозначим через разложим левую и правую части равенства (4) по степеням h. Для левой части будем иметь
Правую часть рассмотрим как сложную ф-цию переменной h и произведем разложение в нуле. Будем иметь Разложение в левых и правых частях слагаемые совпадают
Т.о. для определения 4 параметров метода получаем
Задавая произвол образом
Оценка погрешности и сходимость одношаговых методов решения задачи Коши. Рассмотрим
Здесь
Экстраполяц. метод Адамса решения задачи Коши. Рассмотрим задачу Коши
После подстановки и интегрирования получим
Здесь На основании теоремы о среднем отсюда получим
Отбрасывая в (9) остаточный член и переходя к приближенным значениям, получаем расчетную формулу где
|
||||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 671; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.54.190 (0.007 с.) |

 (1)
(1)  , y(a)=y0 (2). Будем предполагать, что задача (1)(2) на
, y(a)=y0 (2). Будем предполагать, что задача (1)(2) на 
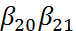
 )
)







 .
. (3).
(3). интегральную кривую уравнения (1), проход через точку
интегральную кривую уравнения (1), проход через точку  , удовлетворяющую условию
, удовлетворяющую условию  . Подставляя ее в (3) получим
. Подставляя ее в (3) получим  (4)
(4) , где
, где  , где
, где  ,
, 

 .
.
 легко найдем остальные парам-ы
легко найдем остальные парам-ы  т.о. при q=1 получим бесконеч. методов Рунге-Кутта 2-го порядка точн-и. Иногда исп. термин однопараметр-ое семейство Рунге-Кутта. При
т.о. при q=1 получим бесконеч. методов Рунге-Кутта 2-го порядка точн-и. Иногда исп. термин однопараметр-ое семейство Рунге-Кутта. При  ,
,  ,
,  получаем метод Коши Эйлера.
получаем метод Коши Эйлера. (1)
(1) 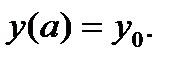 (2). Пусть задача Коши (1), (2) имеет точное решение
(2). Пусть задача Коши (1), (2) имеет точное решение 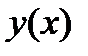 . На отрезке
. На отрезке  зададим сетку
зададим сетку  . Для численного решения задачи Коши (1), (2) будем использ. одношаг. метод с расчетной формулой вида
. Для численного решения задачи Коши (1), (2) будем использ. одношаг. метод с расчетной формулой вида  (3). Приближ. значения решения задачи Коши в узлах сетки
(3). Приближ. значения решения задачи Коши в узлах сетки  , получаемые реально при вычисл. по формуле (3), обозн. через
, получаемые реально при вычисл. по формуле (3), обозн. через  . Эти значения удовл. Рав-ам
. Эти значения удовл. Рав-ам  (4). Здесь
(4). Здесь  - вычислит. погр-ть на шаге при вычислениях по формуле (3). Обозначим через
- вычислит. погр-ть на шаге при вычислениях по формуле (3). Обозначим через  точные решения задач Коши
точные решения задач Коши  (5),
(5),  (6). Подставляя в (3)
(6). Подставляя в (3)  имеем
имеем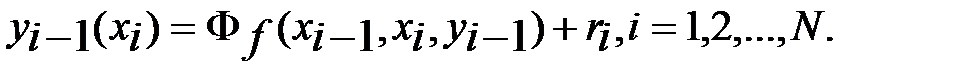 (7). Здесь
(7). Здесь  - погр-ть метода на соотв. шаге. Вычитая из равенств (7) равенства (4), получим общую погр-ть на шаге
- погр-ть метода на соотв. шаге. Вычитая из равенств (7) равенства (4), получим общую погр-ть на шаге  . (8). Проведем оценку погрешности
. (8). Проведем оценку погрешности 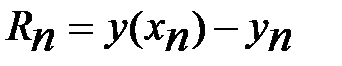 решения задачи Коши, получаемого по расчетной формуле (3) в узле
решения задачи Коши, получаемого по расчетной формуле (3) в узле  . Очевидно, искомую погрешность можно записать в виде
. Очевидно, искомую погрешность можно записать в виде  . (9). Здесь
. (9). Здесь  - неустранимая погр-ть решения в узле
- неустранимая погр-ть решения в узле  , которая вызвана погр-ю
, которая вызвана погр-ю  задания нач. условия; а по-ть
задания нач. условия; а по-ть  вызвана пог-ми метода и вычислит.
вызвана пог-ми метода и вычислит.  на соотв. шаге. Для проведения преобразований в формуле (9) нам понадобится след. лемма. Лемма. Пусть
на соотв. шаге. Для проведения преобразований в формуле (9) нам понадобится след. лемма. Лемма. Пусть  - решения д. у.
- решения д. у. 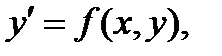 где
где  - непрерывная и непрерывно диф-я по переем.
- непрерывная и непрерывно диф-я по переем. 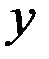 ф-я. Тогда
ф-я. Тогда 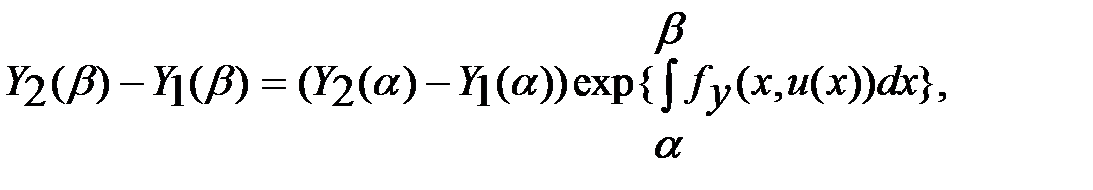 (10), где
(10), где  заключено между
заключено между  и
и  . Док-во. По условию леммы
. Док-во. По условию леммы  ,
,  .
. 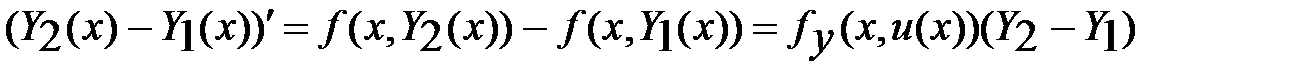 . Здесь
. Здесь  заключено между
заключено между  и
и  . Так как
. Так как  явл. на расс-ом отрезке непрерывной ф-ей, то
явл. на расс-ом отрезке непрерывной ф-ей, то  , а отсюда следует (10). Лемма доказана. Использ. доказ. лемму, преобр. выражение (9) к виду
, а отсюда следует (10). Лемма доказана. Использ. доказ. лемму, преобр. выражение (9) к виду 
 . (11)
. (11) заключено между
заключено между  и
и  , а
, а  - между
- между  и
и  .
.  Пусть имеют место оценки
Пусть имеют место оценки и
и  в рассматр. области изменения аргументов. Тогда из (11) имеем следующую оценку искомой погр-ти
в рассматр. области изменения аргументов. Тогда из (11) имеем следующую оценку искомой погр-ти  . Обознач.
. Обознач.  . Т.к.
. Т.к.  , то оценку можно переписать в виде
, то оценку можно переписать в виде . (12). Введем обозначение
. (12). Введем обозначение  . На основании оценки (12) сформулируем достаточные условия сходимости. Одношаговый метод с расчетной формулой (3) сходится, если
. На основании оценки (12) сформулируем достаточные условия сходимости. Одношаговый метод с расчетной формулой (3) сходится, если  ,
,  при
при  . (13). Итак, получена искомая оценка погрешности (12) и достаточные условия сходимости (13).
. (13). Итак, получена искомая оценка погрешности (12) и достаточные условия сходимости (13). (1)
(1) (2). Пусть задача Коши (1), (2) имеет точное решение
(2). Пусть задача Коши (1), (2) имеет точное решение  . На отрезке
. На отрезке  построим с шагом
построим с шагом  равномерную сетку
равномерную сетку  (3). Для любой гладкой функции
(3). Для любой гладкой функции  выполняется равенство
выполняется равенство  . (4) Перейдем к новой переменной интегрирования
. (4) Перейдем к новой переменной интегрирования 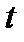 по правилу
по правилу  :
:  . (5) Возьмем в качестве узлов интерполяции узлы сетки
. (5) Возьмем в качестве узлов интерполяции узлы сетки  и заменим в (5) подынт. Ф-ю
и заменим в (5) подынт. Ф-ю  интерполяц. многочленом Ньютона для интерполирования в конце таблицы
интерполяц. многочленом Ньютона для интерполирования в конце таблицы
 , (6) где остаточный член интерполяционного многочлена
, (6) где остаточный член интерполяционного многочлена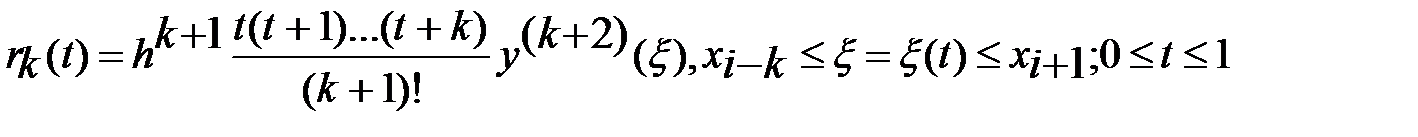 .
.
 , (7).
, (7). ,
,  .
. , из которого следует оценка
, из которого следует оценка  , (8), где
, (8), где 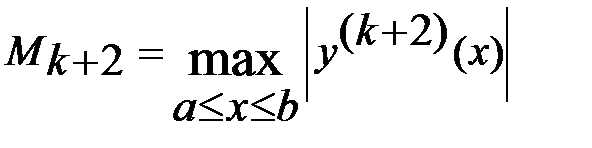 . Возьмем теперь в (7) в качестве
. Возьмем теперь в (7) в качестве 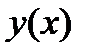 интегральную кривую
интегральную кривую  диф-го уравнения (1), удовлетворяющую условию
диф-го уравнения (1), удовлетворяющую условию  . С учетом, что
. С учетом, что 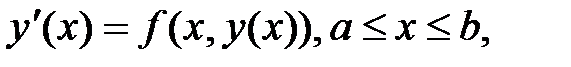 равенство (7) примет вид
равенство (7) примет вид 
 , (9)
, (9) , (10)
, (10) . Метод с расчетной формулой (10) называют экстраполяционным методом Адамса. Погрешность метода на шаге или погрешность расчетной ф-лы метода опр-ся остаточным членом
. Метод с расчетной формулой (10) называют экстраполяционным методом Адамса. Погрешность метода на шаге или погрешность расчетной ф-лы метода опр-ся остаточным членом 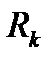 соотв-ей точной формулы (9). Экстраполяционный метод Адамса с расчетной формулой (10) является явным
соотв-ей точной формулы (9). Экстраполяционный метод Адамса с расчетной формулой (10) является явным  -шаговым и имеет
-шаговым и имеет  порядок точности. Отметим, что в случае
порядок точности. Отметим, что в случае  мы получаем одношаговый метод Эйлера.
мы получаем одношаговый метод Эйлера.


