
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Наилучшие приближения в линейном нормированном пространстве.Содержание книги
Поиск на нашем сайте Пусть
Будем аппроксимировать ф-ию f ф-ей При этом Теорема. В ЛНП элемент наилучшего приближения всегда существует. Д-во. Обозначим Для приращения функции
На единичной сфере
Заметим, что ЛНП наз-ся строго нормированным, если из условия Интерполяционные сплайны. Сплайн-функция - кусочно-полиномиальная ф-ия, определ-ая на [a;b], имеющ. на нем некот.число непрерывных произв-ых.В выч. практике исп-тся кубические сплайны(к.с.)- сплайн опр-ся с помощью многочленов 3-ей степени. Рассмотрим интерполяц-ый к.с.(и.к.с.) для ф-ии f(x), непрерывной на [a;b]. На[a;b]сетка: a=x0<...<xN=b (1),обознач. И.к.с для f(x) и данного набора узлов (1)-ф-ия S(x),удовлетв-ая условиям: 1) на каждом сегменте [xi-1;xi],i=1,..,N, S(x) -мночлен 3-ей степ-и 2) S(x), ее первая и вторая производные непрерывны на [a;b]; 3) 3) - усл-ие интерполирования. В 4) задаются граничные усл-ия. Теорема. Для любой непрерывной ф-ии f(x) при любом наборе узлов (1) и.к.с S(x) сущ-ет и является единственным. Д-во. существования - конструктивным методом. На каждом из отр. Доопределим, Из 2) для ф-ии S(x) во внутр-х узлах сетки Si-1(xi-1)=Si(xi-1), i=2..N и условия интерполир-ия
Из усл-ия непрерывности 1-ой производной
Из усл-ия непрерывности
Т.о., получена замкнутая сис-ма ур-ий (3), (4), (5) для опр-ия коэфф-ов к.с.. Покажем,ч. сис-ма имеет 1 решение. Перепишем (3) в виде
Существование и единственность кубического сплайна. Теорема. Для любой непрерывной функции Д-во существования проведем конструктивным методом. На каждом из отрезков
где Коэффициенты Доопределим, кроме того, - 2) функция и граничных условий: - 4) Из условия непрерывности функции
Из условия непрерывности первой производной Условия непрерывности второй производной приводят к уравнениям где доопределено Таким образом, получена замкнутая система уравнений (3), (4), (5) для определения коэффициентов кубического сплайна. Покажем, что эта система имеет единственное решение. Перепишем уравнения (3) в виде Комбинируя два соседних уравнения вида (6), имеем
Далее, из уравнения (5) имеем
|
||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 758; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

 - линейное нормированное пространство и в нем задана последовательность линейно независимых элементов
- линейное нормированное пространство и в нем задана последовательность линейно независимых элементов  . Рассмотрим множество линейных комбинаций
. Рассмотрим множество линейных комбинаций , где
, где  - числовые коэффициенты.
- числовые коэффициенты.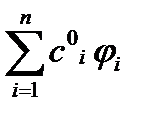 т.о., что
т.о., что  (1)
(1) наз-ть эл-ом наилучшего приближения.
наз-ть эл-ом наилучшего приближения. . Покажем, что функция
. Покажем, что функция  непрерывно зависит от своих аргументов.
непрерывно зависит от своих аргументов. используя для нормы аксиому треугольника, имеем
используя для нормы аксиому треугольника, имеем (2).Отсюда получаем оценку:
(2).Отсюда получаем оценку: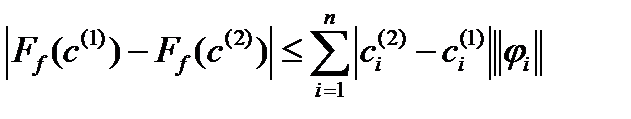 , из которой следует непрерывность ф-ии
, из которой следует непрерывность ф-ии  , которая является замкнутым ограниченным множеством, непрерывная функция
, которая является замкнутым ограниченным множеством, непрерывная функция  принимает свое минимальное значение. Обозначим его через
принимает свое минимальное значение. Обозначим его через  . В силу аксиомы тождества для нормы и линейной независимости элементов
. В силу аксиомы тождества для нормы и линейной независимости элементов 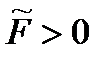 . В случае произвольного набора коэффициентов имеем
. В случае произвольного набора коэффициентов имеем . (3)Выберем число
. (3)Выберем число 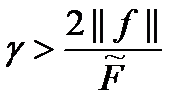 . Ф-ия
. Ф-ия  непрерывна на шаре
непрерывна на шаре 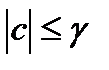 , поэтому достигает на нём своей нижней грани
, поэтому достигает на нём своей нижней грани 
 (4). Вне шара, т.е. при
(4). Вне шара, т.е. при  с учётом (3) и (4) имеем оценку:
с учётом (3) и (4) имеем оценку:  Показали, что на шаре
Показали, что на шаре 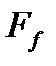 достигает своего минимума
достигает своего минимума  , а вне шара
, а вне шара  .
. следует, что
следует, что 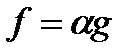 , где
, где  число.
число.
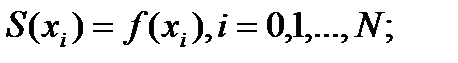 4)
4) 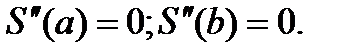
 б. искать ф-ию S(x)= Si(x) -многочлен 3-ей степени (
б. искать ф-ию S(x)= Si(x) -многочлен 3-ей степени ( )
)  (2) где
(2) где  - коэфф-ты. ai найдем из усл-ий интерп-ния
- коэфф-ты. ai найдем из усл-ий интерп-ния 
 Остальные коэфф-ты найдем из условий непрерывности 2) и граничных условий 4).
Остальные коэфф-ты найдем из условий непрерывности 2) и граничных условий 4). имеем
имеем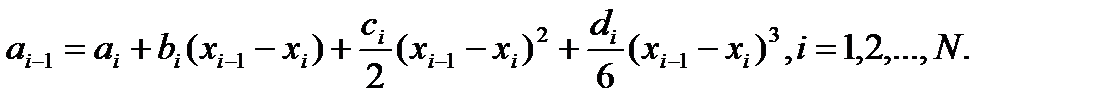 Пусть
Пусть 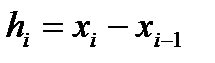 =>
=>  (3)
(3) во внутр-их узлах сетки
во внутр-их узлах сетки  имеем
имеем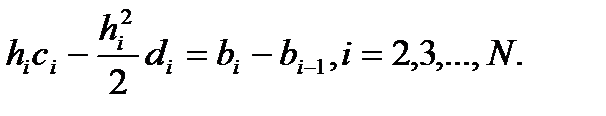 (4)
(4)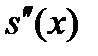 во внутр-их узлах сетки
во внутр-их узлах сетки  и граничных условий
и граничных условий 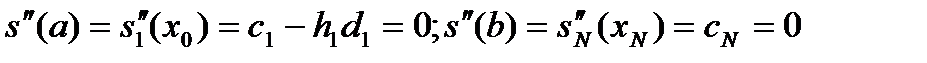 -->
--> (5) где доопределено c0=0;
(5) где доопределено c0=0; (6). Комбинируя 2 соседних ур-ия (6):
(6). Комбинируя 2 соседних ур-ия (6): Подставляя найденное выражение для bi-bi-1 в пр. часть(4) получаем (7):
Подставляя найденное выражение для bi-bi-1 в пр. часть(4) получаем (7): Из (5):
Из (5): Подставляя это в (7), получаем сис-му ур-ний для ci :
Подставляя это в (7), получаем сис-му ур-ний для ci : 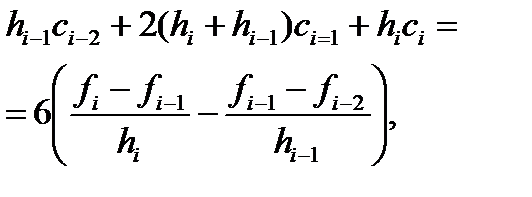
 (8) В силу диагонального преобладания (8) имеет 1 решение. Т.к. матрица сис-мы трехдиагональная, решение - методом прогонки, кот. в данном случае устойчива.
(8) В силу диагонального преобладания (8) имеет 1 решение. Т.к. матрица сис-мы трехдиагональная, решение - методом прогонки, кот. в данном случае устойчива. 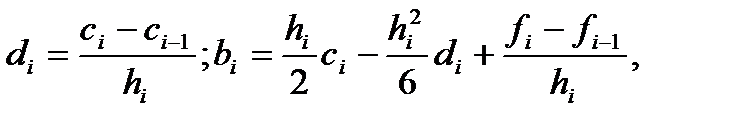
 Ч.т.д.
Ч.т.д. при любом наборе узлов
при любом наборе узлов  (1) интерполяционный кубический сплайн
(1) интерполяционный кубический сплайн 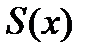 существует и является единственным.
существует и является единственным.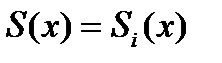 в виде многочлена третьей степени
в виде многочлена третьей степени найдем из условий интерполирования
найдем из условий интерполирования 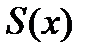 , а также ее первая и вторая производные непрерывны на [a;b]
, а также ее первая и вторая производные непрерывны на [a;b] во внутренних узлах сетки
во внутренних узлах сетки  и условия интерполирования
и условия интерполирования 
 в правую часть уравнения (4), получим
в правую часть уравнения (4), получим


