
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общая задача интерполирования алгебраическими многочленами. Интерполяционный многочлен Эрмита с узлами кратности 2.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Общая задача интерполирования обобщенными многочленами формулируется следующим образом. Для функции
Ограничимся рассмотрением здесь случая, когда
Рассмотрим разность Исходная задача сведена к построению многочлена Продиф-руем равенство (2): Дифференцируя равенство (2) дважды, получим
Для построения многочлена Многочлен Проведем построение многочлена Эрмита для случая, когда все узлы имеют одинаковую кратность, равную двум. Условия (1) при этом принимают вид
Используя формулы (2) и (3), получим
Т.о., построен искомый интерпол-ный многочлен Эрмита
Проведем в выражении (6) алгебраические преобразования. Учтем, что
Рассмотрим выражение в фигурных скобках
Полагая в (8)
Заменим в (7) многочлен
12. Некорректность задачи численного диф-я в пр-ве ℂ. Решение поставленной задачи можно провести с использованием интерполяционного многочлена Лагранжа Таким образом, производная многочлена Покажем, что в общем случае малая разность между двумя функциями на отрезке еще не означает, что малой будет и разность их производных на этом отрезке. В качестве примера рассмотрим функции а расстояние между их производными в этом пр-ве Примеры формул численного дифференцирования В качестве примера рассмотрим использование для интерполирования в начале таблицы интерполяционного многочлена Ньютона:
Дифференцируя приближенное равенство
Третья производная многочлена третьей степени является константой При неравноотстоящих узлах для построения формул численного дифференцирования используются интерполяционный многочлен Лагранжа
|
||||
|
Последнее изменение этой страницы: 2016-04-06; просмотров: 760; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.209.114 (0.006 с.) |

 и набора попарно неравных узлов
и набора попарно неравных узлов  требуется построить обобщенный многочлен
требуется построить обобщенный многочлен  по системе функций
по системе функций  так, чтобы значения обобщенного многочлена и его производных до определенного порядка в узлах совпадали с соотв-щими значениями функции и ее производных:
так, чтобы значения обобщенного многочлена и его производных до определенного порядка в узлах совпадали с соотв-щими значениями функции и ее производных:
 .
. , то есть, общей задачей интерполирования алгебраическими многочленами. Для функции
, то есть, общей задачей интерполирования алгебраическими многочленами. Для функции  , удовлетворяющий условиям
, удовлетворяющий условиям . (1)
. (1) , где
, где  - интерпол-ный многочлен Лагранжа для
- интерпол-ный многочлен Лагранжа для  при
при  , то
, то  . (2)
. (2) .
. . Для узлов
. Для узлов  , в которых заданы значения производной
, в которых заданы значения производной  отсюда имеем
отсюда имеем  . (3)
. (3)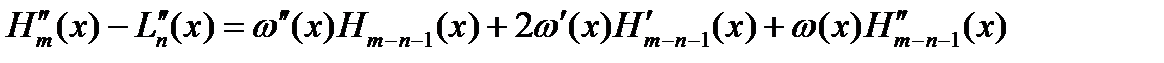 Отсюда для узлов
Отсюда для узлов  , имеем
, имеем Далее, приходим к задаче построения многочлена
Далее, приходим к задаче построения многочлена  степени
степени  , удовл. усл.
, удовл. усл.  . (4)
. (4) и является единственным.
и является единственным. узлов.
узлов. . (5)
. (5) ;
;
 .
. . (6)
. (6) и
и Тогда формула (6) примет вид
Тогда формула (6) примет вид (7)
(7) . Это многочлен степени
. Это многочлен степени  . При этом
. При этом 
 Следовательно, рассматриваемый многочлен представляется в виде
Следовательно, рассматриваемый многочлен представляется в виде  . (8)
. (8) , имеем
, имеем  и
и  . Из условия
. Из условия находим
находим . Подставляя полученные выражения коэффициентов в (8), имеем
. Подставляя полученные выражения коэффициентов в (8), имеем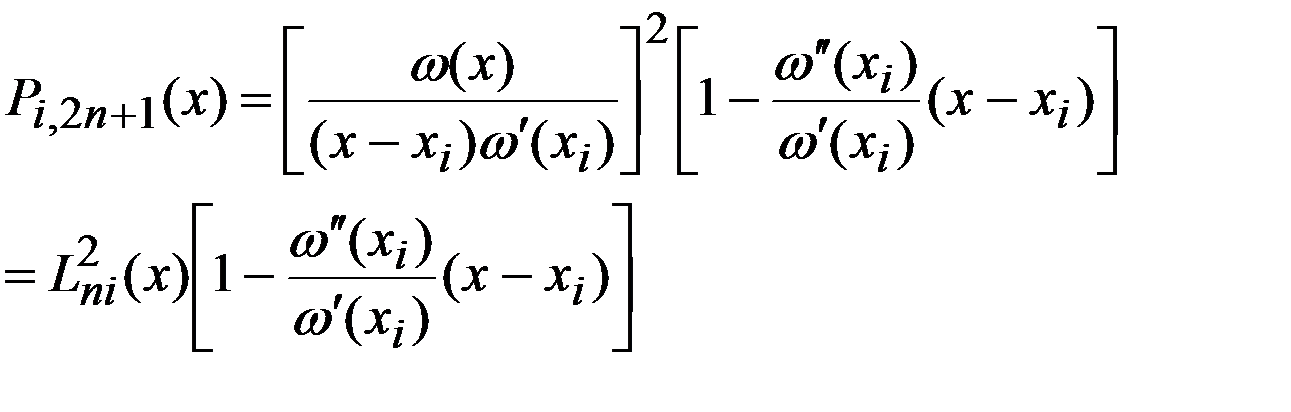 .
. в фигурных скобках найденным выражением, тогда для многочлена Эрмита с узлами кратности 2 получим окончательное выражение
в фигурных скобках найденным выражением, тогда для многочлена Эрмита с узлами кратности 2 получим окончательное выражение . (9)
. (9)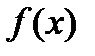 задана на отрезке
задана на отрезке  таблицей значений
таблицей значений 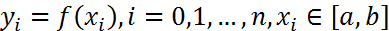 и надо найти приближенное значение ее производной в некоторой точке этого отрезка.
и надо найти приближенное значение ее производной в некоторой точке этого отрезка. порядка n, который приближает функцию с погрешностью
порядка n, который приближает функцию с погрешностью  . Дифференцируя равенство
. Дифференцируя равенство  , (1) m раз имеем погрешность
, (1) m раз имеем погрешность  . (2)
. (2) приближает производную функции
приближает производную функции  с погрешностью
с погрешностью  , т.е., приближенное равенство
, т.е., приближенное равенство 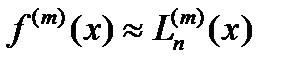 (3) имеет погрешность
(3) имеет погрешность  ℂ
ℂ  . Найдем отклонение
. Найдем отклонение  от
от  . Расстояние между этими функциями в пространстве ℂ
. Расстояние между этими функциями в пространстве ℂ 
 . Некорректность в пространстве ℂ задачи численного дифференцирования заключается в том, что из сходимости в этом пространстве последовательности функций не следует, что последовательность производных этих функций также будет сходиться.
. Некорректность в пространстве ℂ задачи численного дифференцирования заключается в том, что из сходимости в этом пространстве последовательности функций не следует, что последовательность производных этих функций также будет сходиться. .
. будем иметь:
будем иметь: .В случае
.В случае  формула приобретает вид
формула приобретает вид  . Для второй производной получаем соответственно
. Для второй производной получаем соответственно  и
и  .
.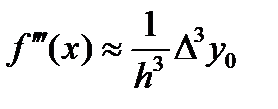 .
. и интерполяционная формула Ньютона с разделенными разностями
и интерполяционная формула Ньютона с разделенными разностями .
.


