
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Деякі задачі, що не розв’язуються в квадратних радикалах.Содержание книги
Поиск на нашем сайте 1. Задача про подвоєння куба. Побудувати ребро куба, об’єм якого вдвічі більше за об’єм даного куба. 2. Задача про трисекцію кута. Поділити даний кут на три рівні частини. 3. Задача про побудову правильного семикутника. Побудувати правильний семикутник, вписаний в одиничний круг. 4. Задача про квадратуру круга. Побудувати квадрат, рівновеликий даному кругу. Розв’язання цих задач зводиться до рівняння, що не розв’язуються в квадратних радикалах. Тому вони не можуть бути побудованими за допомогою циркуля і лінійки. Отже, розв’язання конструктивної задачі за допомогою циркуля і лінійки і розв’язність алгебраїчного рівняння в квадратних радикалах – це два аспекти однієї і тієї ж проблеми. Контрольні питання для самоперевірки. 1. Дайте означення квадратичного розширення поля Р. 2. Доведіть, що розширення К поля Р другого степеня є квадратичне розширення поля Р. 3. Які числа називаються піфагоровими? 4. Дайте означення основного поля. 5. Дайте означення розв’язності рівняння в квадратних радикалах. 6. Доведіть, що всі числа, які можна виразити в квадратних радикалах через числа поля Р, є алгебраїчними над цим полем. 7. Сформулюйте критерії розв’язності в квадратних радикалах. 8. Доведіть, що задачу про трисекцію нуля не можна побудували циркулем та лінійкою. 9. Доведіть, що задачу про побудову правильного n-кутника не можна побудували циркулем та лінійкою. 10. Доведіть, що рівняння 11. Покажіть, що рівняння Література: [4] гл.8, §35 [3], гл.17 §4. Плани-конспекти практичних занять Семестр ІV Заняття 1. Тема: Групи. Підгрупи. Розклад групи за підгрупою. Теорема Лагранжа. Аудиторні завдання. 1. а) Перевірити, чи утворюють наступні множини групу відносно вказаних операцій. б) Встановити, які з груп абелеві, циклічні. в) Побудувати таблиці Келі для операцій, визначених на заданих множинах: G 1 = < –1, і, – і > (×), де i 2 = –1; G 2 = < 1, –1, і, j, k, – і, – j, – k > (×), i 2 = j 2 = k 2 = –1; i × j = k; i × k =– j; j × k = i; j × i =– k; k × i = j; k × j =– i;
G 5 = < z = a + bi; a, b Î R, i 2 = –1> (+); G 6 = < z = a + bi; a, b Î R, z ¹0, i 2 = –1> (×). 2. Знайти усі підгрупи групи G 2. 3. Довести, що група простого порядку р циклічна. 4. Розкласти групу G 5 на суміжні класи за підгрупою A =< z =cosj+ i sinj> та дати їх геометричну ілюстрацію. 5. Довести, що група G порядку р 2 (р – просте число) – абелева. Домашні завдання. [10] cтор. 14 № 1.1.3: № 1 (а–к), стор. 30 № 1.2.3, № 1, 3, 9, 10, 12 (а, б, і). Заняття 2. Тема: Нормальний дільник. Фактор-група. Спряжені елементи та класи спряжених елементів. Гомоморфізми груп. Аудиторні завдання. 1. Дати опис усіх не ізоморфних груп 6-го та 8-го порядку. 2. Показати, що усі підгрупи групи кватерніонів – її нормальні дільники. 3. Нехай G – мультиплікативна група комплексних чисел з модулем, рівним одиниці: G =< z =cosj+ i sinj, | z |=1> і Н – її підгрупа – коренів n –го степеня з одиниці: 4. Для мультиплікативної групи дійсних матриць порядку n довести твердження: а) фактор-група групи дійсних матриць за підгрупою матриць з визначником, рівним одиниці, ізоморфна мультиплікативній групі дійсних чисел, відмінних від нуля; б) фактор-група групи дійсних матриць за підгрупою матриць з додатними визначниками є циклічною групою другого порядку. 5. Знайти розклад групи S 3 та групи кватерніонів на класи спряжених елементів. Домашні завдання. [10] cтор. 30 № 1.2.3: № 12 (в, г, д, з, і), № 13, № 14.
Заняття 3. Тема: Кільця та поля. Аудиторні завдання. 1. З‘ясувати, які з наступних числових множин є кільцями (але не полями) та які полями відносно арифметичних операцій додавання та множення: а) цілі числа, що кратні даному числу а; б) числа вигляду в) числа вигляду г) числа вигляду 2. З‘ясувати, які з наступних множин є кільцями (але не полями) і які полями відносно додавання та множення матриць: а) матриці n –ого порядку з цілими елементами; б) матриці вигляду в) матриці вигляду 3. Показати, що в кільці квадратних матриць n –oго порядку з дійсними елементами, дільниками нуля є вироджені і тільки вироджені матриці. 4. Показати, що пари (а, b) цілих чисел з операціями, заданими рівностями (a 1, b 1) + (a 2, b 2) = (a 1 + a 2, b 1 + b 2), (a 1, b 1) × (a 2, b 2) = (a 1 × a 2, b 1 × b 2). утворюють комутативне кільце. Знайти усі дільники нуля цього кільця. 5. Показати, що пари (а, b) раціональних чисел з операціями, заданими рівностями (a 1, b 1) + (a 2, b 2) = (a 1 + a 2, b 1 + b 2), (a 1, b 1) × (a 2, b 2) = (a 1 a 2 + b 1 b 2, a 1 b 2 + b 1 a 2). утворюють комутативне кільце. Знайти усі дільники нуля цього кільця. 6. Показати, що множина матриць вигляду 7. Показати, що множина матриць вигляду 8. Показати, що множина матриць вигляду Вказівки: 1. При розв’язуванні задач 4 і 5 слід знайти ненульові розв'язки рівняння (a, b)×(x, y) = (0, 0). 2. При розв’язуванні задачі 8 скористуйтеся тим, що задана множина матриць утворює кільце з дільниками нуля. Домашні завдання. [10] cтор. 63 № 2.1.3: № 1 (a 1, a 2, a 3, a 4), № 2 (b 1, b 2); 4, 5.
Заняття 4. Тема: Ідеали кільця. Фактор-кільце. Прості та складені елементи області цілісності. Евклідові кільця. Аудиторні завдання. 1. Показати, що множина а) є підкільце в кільці К; б) є власний ідеал кільця К. 2. Чи є ідеалами такі підмножини: а) множина б) множина в) множина г) множина 3. Побудувати фактор-кільце 4. Довести, що характеристикою області цілісності є або нуль, або просте число. 5. Простим чи складеним є ціле гауссове число 3+2 і. 6. Довести, що число 4 в кільці 7. Встановити гомоморфне відображення довільного кільця К на фактор-кільце 8. Довести, що ізоморфними між собою є такі кільця: а) б) в) 9. Довести, що в кільці 10. Довести, що дані кільця є евклідовим: а) кільце б) кільце Вказівки: 1. При розв’язуванні задачі 3 скористатися означенням фактор-кільця
Тоді
2. При розв’язанні задачі 5 розглянути кільце Z [ i ], дільниками одиниці в якому є числа 1, –1, і, – і, та скористатися нормою цілого гауссового числа. 3. При розв’язанні задачі 6 знайти спочатку дільники одиниці в 4. В задачі 4 задати відображення множини К на множину 5. В задачі 9 скористатися означенням простого або нерозкладного, незвідного елемента: елемент а області цілісності К називається простим, якщо: а) a ¹0; б) a не є дільником одиниці; в) а, крім дільників одиниці і асоційованих з ним, ніяких інших дільників не має. Домашні завдання. [10] cтор. 66 № 2 (в 2, в 3, в 4, в 5, в 7, в 8); стор. 85, № 2.2.3, № 1 (а–д), 5.
Заняття 5. Тема: Кільце многочленів від однієї змінної над даним полем. Аудиторні завдання. 1. Довести, що многочлени від однієї змінної з коефіцієнтами з будь-якого поля Р утворюють кільце. 2. Довести, що в кільці многочленів Р [ х ] будь-який ідеал – головний. 3. Знайти найбільший спільний дільник многочленів: f (x) = x 7–3 x 6 +5 x 5 –7 x 4 +7 x 3 –5 x 2 + x –1, g (x) = 7 x 6 –18 x 5 +25 x 4 –28 x 3 +21 x 2 –10 x +3 та підібрати многочлени j(x) i y(x) так, щоб виконувалася рівність: f (x)×j(x) + g (x)×y(x) = 1. 4. Знайти многочлен найменшого степеня, що дає в остачі (x +1) при діленні на (x –1)2 і (2 x –1) при діленні на (x –3)2. 5. Розкласти многочлен f (x) за степенями двочлена (x – a), а також знайти значення многочлена і усіх його похідних при x = a: f (x) = x 4 +3 x 3 –8 x 2 +4 x –1, a =2. 6. Знайти кратність множника (x + a) для многочлена x 5 +7 x 4 +16 x 3 +8 x 2 –16 x –16, a =2. 7. Відокремити кратні множники многочлена f (x) = x 6 – 6 x 4 – 4 x 3 +9 x 2 +12 x +4. Домашні завдання. [10] cтор. 205 № 3 (б, в); № 5 (в, д); № 6 (б, в); № 7 (г, д); № 8 (б, в); № 9; № 10 (а, в). Заняття 6. Тема: Корені многочлена.
Аудиторні завдання. 1. Знайти значення многочлена f (x) = x 6 + 3 x 4 + 2 x 3 – 9 x 2 +5 при x = – 2. 2. З‘ясувати, чи є коренями многочлена f (x) = 2 x 4 + 3 x 3 – 4 x 2 +2 x –3 числа a = 1; 2. 3. Знайти кратність кореня x = 5 многочлена f (x) = x 5 – 15 x 4 + 76 x 3 – 140 x 2 +75 x –125. 4. Визначити а і b так, щоб многочлен f (x) = x 5 – 15 x 4 + ax 2 + bx +1 мав число – 2 коренем не нижче 2-ої кратності. 5. Знайти многочлен найменшого степеня, що має корені 2; і та двократний корінь – 1. 6. Визначити а, b, с так, щоб вони були коренями многочлена f (x) = x 3 – ax 2 + bx – c. 7. Знайти необхідну та достатню умову, при якій корені многочлена f (x) = x 3 + ax 2 + bx + c утворюють геометричну прогресію. 8. Сума двох коренів многочлена f (x) = 2 x 3 – x 2 – 7 x + l дорівнює 1. Знайти l. 9. Знати суму кубів коренів многочлена f (x) = xn + a 1 xn –1 + … + an. 10. Нехай f (x) – многочлен з дійсними коефіцієнтами. Доведіть наступні твердження: а) якщо числа f (a) і f (b) різних знаків, то в інтервалі (а, b) міститься непарна кількість коренів многочлена f (x); б) якщо f (a) і f (b) – числа одного знаку, то в інтервалі (а, b) міститься парна кількість коренів многочлена f (x). 11. Відомо, що числа a1, a2 , …, a n є коренями многочлена f (x) = a 0 xn + a 1 xn –1 + … + an. Знайти многочлен, що має своїми коренями числа: а) – a1, – a2 , …, – a n; б) 12. Побудувати поле розкладу многочлена (вказати вид елементів цього поля) f (x) = x 6 – 15 x 4 + 71 x 2 – 105; f (x)Î Q [ x ]. Домашні завдання. [10] cтор. 228 № 4, 5, 7, 10, 9.
Заняття 7. Тема: Многочлени від n змінних. Аудиторні завдання. 1. Довести, що многочлени від n невідомих x 1, x 2, …, xn над Р утворюють комутативне кільце. 2. Виразити многочлен 3. Виразити многочлен 4. Знайти суму кубів коренів рівняння x 4 + 2 x 3 + x 2+5 x + 3 = 0. 5. Розкласти на множники многочлен f (x, y, z) = x 3 + y 3 + z 3 – 3 xyz. 6. Скласти многочлен, що має своїми коренями куби коренів многочлена f (x) = x 2 + px + q. Домашні завдання. [10] cтор. 253 № 5, 7, 8, 9.
Заняття 8. Тема: Результант многочленів. Позбавлення від ірраціональності в знаменнику дробу.
Аудиторні завдання. 1. Обчислити результант многочленів f (x) = 2 x 3–3 x 2+2 x +1; g (x) = x 2+ x +3. 2. Розв’язати систему рівнянь:
3. При яких значеннях l многочлени f (x) = x 3– l x +2 і g (x) = x 2 + l x +2 мають спільний корінь? 4. Знайти площу і радіус круга, описаного навколо трикутника, сторони якого дорівнюють кореням кубічного рівняння x 3 – ax 2 + bx – c = 0. Вказівка: Виразити площу і радіус круга у вигляді симетричних функцій від його сторін. 5. Позбавитися від ірраціональності в знаменнику наступних дробів: а) б) Домашні завдання. [10] cтор. 252 № 14, 17, 18, 19.
Заняття 9. Тема: Многочлени над числовими полями. Розширення полів. Аудиторні завдання. 1. Знайти раціональні корені многочленів а) f (x) = x 4 + x 3 – 11 x 2 – 5 x + 30; б) f (x) = 4 x 5 + 12 x 4 + x 3 + 6 x 2 +10 x + 3. 2. Розв’язати рівняння: а) x 4 – 2 x 3 + 6 x 2 – 4 x + 8 = 0; б) x 3 – 6 x 2 + 30 x – 25 = 0. 3. Відокремити дійсні корені многочлена f (x) = x 5 + 5 x 4+7 x 3 +2 x 2 –2 x –1. 4. Показати, що число a є алгебраїчним відносно поля R та знайти його степінь n.
5. Знайти загальний вигляд чисел з простого алгебраїчного розширення поля R за допомогою алгебраїчного числа a, якщо 6. Побудувати поле 7. Показати, що складене алгебраїчне розширення Домашні завдання. [10] cтор. 264; № 1, 2, 3, 4; cтор. 231; № 12, 13; cтор. 228; № 3, cтор. 227 № 1 (a2, a14, a7), № 2 (б3, б4, б10, б12).
Контрольні роботи Контрольна робота № 1 Дано множини відносно добутку
Задачі. 1. Довести, що D – група. 2. Довести, що К – група. 3. Побудувати таблицю Келі для D. 4. Побудувати таблицю Келі для К. 5. Знайти всі твірні елементи для групи D. 6. Знайти всі твірні елементи для групи К. 7. Знайти всі підгрупи і їх твірні в групі D. 8. Знайти всі підгрупи і їх твірні в групі К. 9. Розкласти групу D на класи спряжених елементів. 10. Розкласти групу К на класи спряжених елементів. 11. Розкласти групу D на ліві суміжні класи. 12. Розкласти групу К на ліві суміжні класи. 13. Довести, що в групі К кожна підгрупа – інваріантна. 14. Знайти нормальний дільник в групі D. 15. Побудувати фактор-групу групи К. 16. Побудувати фактор-групу групи D. 17. Довести, якщо | a | = n і ak = 1, то n ділить k. 18. Довести, якщо | g | = n, то " g Î G gk =1 тоді і тільки тоді, коли k ділиться на n. 19. Довести, якщо | G | = pq, p, q – різні прості числа і G – абелева, то в G існує елемент а, | a | = pq. 20. Довести, якщо | G | = pq, p ¹ q – прості числа, то в G існує інваріантна підгрупа. 21. Довести, якщо | G | = p 2, то вона або циклічна, або абелева. 22. Нехай C 1 – підкільце кільця C, I – ідеал кільця C. Довести, що C 1Ç I – ідеал кільця C 1. 23. Довести, що в кільці цілих чисел Z кожен його ідеал – головний. 24. Довести, що при гомоморфізмі j двох кілець K 1 і K 2 j(a – b)= j(a)–j(b). 25. Довести, що при гомоморфізмі j двох кілець K 1 і K 2 j(a –1) = [j(a)]–1 (якщо в K 1 для а існує обернений елемент a –1). 26. Довести, що будь-який ідеал I кільця С є ядром гомоморфізму при відображення кільця С на фактор-кільце C / I. 27. Довести, що підмножина I кільця С є ядром гомоморфізму цього кільця на деяке кільце тоді і тільки тоді, коли I є ідеалом кільця С. 28. Довести, що характеристика будь-якого числового кільця дорівнює нулю. 29. Довести, що найменше підполе будь-якого поля характеристики нуль ізоморфне полю раціональних чисел. 30. Довести, що в кільці Z [ i ] простими є такі елементи: 3; 2 + i. 31. Довести, що в кільці Z [ i ] простими є такі елементи: –3; 2 – i. 32. Довести, що в кільці 33. Довести, що в кільці
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 469; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 ;
;  розв’язуються в квадратних радикалах.
розв’язуються в квадратних радикалах. не розв’язується в квадратних радикалах ні над жодним полем.
не розв’язується в квадратних радикалах ні над жодним полем.

 . Показати, що фактор-група G / H ізоморфна групі G.
. Показати, що фактор-група G / H ізоморфна групі G. , де a, b Î Q;
, де a, b Î Q; , де a, b Î Q;
, де a, b Î Q; , де
, де  – дійсне значення кореня і a 0, a 1, a 2ÎZ.
– дійсне значення кореня і a 0, a 1, a 2ÎZ. з раціональними а і b;
з раціональними а і b; з раціональними а і b.
з раціональними а і b. , де a, b ÎZ, ізоморфна полю, утвореному числами вигляду
, де a, b ÎZ, ізоморфна полю, утвореному числами вигляду  , де a, b Î R, ізоморфна полю комплексних чисел.
, де a, b Î R, ізоморфна полю комплексних чисел. , де a, b Î Z, утворює комутативне кільце (відносно додавання та множення матриць), але це кільце не може бути ізоморфним з жодною числовою множиною з операціями – арифметичне додавання та множення.
, де a, b Î Z, утворює комутативне кільце (відносно додавання та множення матриць), але це кільце не може бути ізоморфним з жодною числовою множиною з операціями – арифметичне додавання та множення. , де a, bÎ К;
, де a, bÎ К;  – кільце,
– кільце, в кільці М (2, Z), якщо m, n Î Z;
в кільці М (2, Z), якщо m, n Î Z; в кільці
в кільці  ;
; в кільці М (2, Z);
в кільці М (2, Z); в кільці М (3, Z).
в кільці М (3, Z). кільця цілих чисел Z за головним ідеалом I =<6>, породженим числом 6. скласти таблиці додавання і множення для елементів фактор-кільця. Знайти всі дільники нуля цього фактор-кільця і обернені елементи.
кільця цілих чисел Z за головним ідеалом I =<6>, породженим числом 6. скласти таблиці додавання і множення для елементів фактор-кільця. Знайти всі дільники нуля цього фактор-кільця і обернені елементи. неоднозначно розкладається в добуток простих множників.
неоднозначно розкладається в добуток простих множників. кільця К за будь-яким його ідеалом І.
кільця К за будь-яким його ідеалом І. i
i  ;
; i
i  ;
; .
. ; г)
; г) 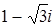 .
. ;
; з нормою
з нормою  .
. для елементів якого введено операції додавання та множення:
для елементів якого введено операції додавання та множення:

 так:
так:  , тобто
, тобто  , де a Î K.
, де a Î K. .
. через основні симетричні многочлени.
через основні симетричні многочлени. через основні симетричні многочлени.
через основні симетричні многочлени.

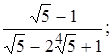 в)
в)  .
.
 .
. .
. є простим алгебраїчним розширенням поля Q.
є простим алгебраїчним розширенням поля Q.


 порушується однозначність розкладу на прості множники.
порушується однозначність розкладу на прості множники.


