
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Властивості симетричних многочленів.Содержание книги Поиск на нашем сайте
1. Множина усіх симетричних многочленів від n змінних над полем Р утворює область цілісності з одиницею. 2. Якщо симетричний многочлен f ( 3. Якщо Означення 7. Симетричні многочлени
..............
називають елементарними симетричними многочленами. Теорема про симетричні многочлени. Будь-який симетричний многочлен f ( Контрольні питання для самоперевірки. 1. Доведіть, що многочлени від n змінних 2. Дайте означення симетричного многочлена. 3. Доведіть, що симетричні многочлени від змінних 4. Які многочлени називають основними симетричними многочленами? 5. Доведіть, що будь-який симетричний многочлен над полем Р від n змінних 6. Доведіть, що будь-який симетричний многочлен від коренів многочлена f(x) раціонально виражається через його коефіцієнти. 7. Обчисліть суму k-x степенів коренів рівняння a0xn+a1xn-1+…+an-1x+an =0, k 8. Доведіть, що кільце многочленів P [ x, y ] над полем Р не є кільцем головних ідеалів. Література: [3], гл. 15, 1, 2; [1], гл. 11, 51, 52; [4], гл. VI, 25, 26.
Лекція 13. Тема: Результант многочленів. План. 1. Результант многочленів. 2. Дискримінант. 3. Розвязання системи алгебраїчних рівнянь.
Короткій зміст лекції Означення 1. Результантом многочленів
називається вираз
де Результант двох многочленів над полем Р є елемент цього ж поля.
Результант у формі Сильвестра.
Результант у формі Сильвестра виражається через коефіцієнти многочленів f і g у вигляді визначника (m+n) порядку:
…………………………… 0 … 0 …
0 …………………………… 0 … 0 0 … 0 …
Для складання визначника Сильвестра достатньо m разів підряд записати коефіцієнти многочлена Отже, результант Теорема 1. Для того, щоб многочлени Означення 2.Дискримінантом
де Теорема 2. Многочлен Теорема 3. Якщо результант многочленів Теорема 4. Якщо многочлени Нехай задано систему двох алгебраїчних рівнянь з двома невідомими з коефіцієнтами із поля Р: Схема виключення невідомих з цієї системи така: 1) упорядковуємо многочлени 2) складаємо результант 3) знаходимо всі корені результанта 4) підставляємо в задану систему замість змінної дістаємо сукупність L систем двох рівнянь з одним невідомим x; 5) розв’язуємо цю сукупність систем рівнянь і складаємо відповідні пари розв’язків. Контрольні питання для самоперевірки. 1. Дайте означення результанта двох многочленів. 2. Як записується результант двох многочленів у формі Сильвестра? 3. Доведіть, якщо многочлени мають спільний корінь, то їх результант дорівнює нулю 4. Дайте означення дискримінанта многочлена. 5. Доведіть, якщо многочлен 6. Як за допомогою результанта розв’язати систему двох рівнянь з двома невідомими? Література:
Лекція 14. Тема: Позбавлення від алгебраїчної ірраціональності в знаменнику дробу. План. 1. Основні методи позбавлення від ірраціональності в знаменнику дробу.
Короткий зміст лекції. Основні факти, на яких ґрунтуються методи позбавлення від ірраціональності в знаменнику дробу: 1. Якщо 2. Поле Нехай
Розглянемо деякі способи розв’язання цієї задачі. I.Так як степінь g(x) =m Тому має місце рівність:
де При
звідси, Якщо h(x) має степінь
II. Застосування формул скороченого множення:
III. Якщо в знаменнику дробу є кілька радикалів, то їх можна поступово позбуватися одним із вище розглянутих способів. IV. Застосування елементарних симетричних многочленів та степеневих сум. Контрольні питання для самоперевірки 1. В чому полягає задача позбавлення від ірраціональності в знаменнику дробу? 2. На яких основних фактах ґрунтується розв’язання цієї задачі? 3. Назвіть основні способи розв’язання даної задачі. 4. Позбавтеся від алгебраїчної ірраціональності в знаменниках дробів:
Література:
Лекція 15. Тема: Многочлени над числовими полями. План. 1. Многочлени над полем комплексних чисел. 2. Алгебраїчна замкненість поля комплексних чисел. 3. Розкладання многочлена над полем дійсних чисел у добуток незвідних множників. 4. Рівняння третього і четвертого степенів. Короткий зміст лекції. Нехай f(x) – деякий многочлен над полем P. Якщо степінь Звідси випливає, що для будь-якого многочлена f(x) є Р Означення 1. Поле Р називається алгебраїчно замкненим, якщо кожний многочлен із кільця Отже, поле Р алгебраїчно замкнене, якщо незвідними над полем Р є лише многочлени першого степеня. Якщо будь-який многочлен f є Р Теорема 1. Поле комплексних чисел С алгебраїчно замкнене. Теорема 2. Многочлен непарного степеня над полем R дійсних чисел має хоча б один дійсний корінь. Теорема 3. Кожний многочлен степеня Теорема 4. (Основна теорема алгебри комплексних чисел). Кожний многочлен ненульового степеня з комплексними коефіцієнтами має хоч би один комплексний корінь. Теорема 5. Кожний многочлен степеня >1 є звідним над полем комплексних чисел. Теорема 6. Кожний многочлен n -го степеня над полем комплексних чисел єдиним способом розкладається у добуток лінійних множників над цим полем:
Теорема 7. Многочлен n -го степеня в полі комплексних чисел має точно n - коренів. Оскільки дійсні числа є підполем поля С комплексних чисел, то всі вище перераховані результати стверджуються і для многочленів з дійсними коефіцієнтами, тобто будь–який многочлен n -го степеня з дійсними коефіцієнтами має точно n комплексних коренів. Теорема 8. Кожний многочлен з дійсними коефіцієнтами, степінь якого перевищує 2, звідний над полем R дійсних чисел. Теорема 9. Кожний многочлен f(z) з дійсними коефіцієнтами єдиним способом розкладається над полем R у добуток лінійних многочленів і квадратних трьохчленів:
Розв’язання рівнянь третього степеня:
Підстановкою
в якому відсутній член з Нехай
Накладаємо на Знаходження коренів звелося до розв’язання системи рівнянь
де Тоді Рівняння 4-го степеня.
Метод Феррарі розв’язування рівняння четвертого степеня. До обох частин рівняння додаємо
До обох частин одержаної рівності додамо ще
Підберемо значення t так, щоб права частина останнього рівняння стала новим квадратом вигляду
Після перетворень одержуємо рівняння:
яке є кубічною резольвентою даного рівняння четвертого степеня. Якщо
Корені цих рівнянь дають всі розв’язки рівняння Контрольні питання для самоперевірки. 1. Доведіть теорему про існування кореня многочлена над полем комплексних чисел. 2. Доведіть, що над полем комплексних чисел многочлен n -го степеня має n коренів, якщо кожний корінь рахувати стільки разів, яка його кратність. 3. Доведіть, що над полем комплексних чисел кожен многочлен, степінь якого вище першого, звідний. 4. Яка залежність між коефіцієнтами і коренями многочлена? 5. Доведіть, що для многочлена з дійсними коефіцієнтами комплексно спряженим значенням х відповідають комплексно спряжені значення f(x). 6. Доведіть, що над полем дійсних чисел будь-який многочлен, степеня вище 2, звідний. 7. Доведіть, що многочлен непарного степеня з дійсними коефіцієнтами має хоч би один дійсний корінь. 8. Розв’яжіть кубічне рівняння
9. Розв’яжіть рівняння 4-го степеня
Література:.
Лекція 16. Тема: Відокремлення дійсних коренів многочлена з дійсними коефіцієнтами. План. 1. Межі дійсних коренів. 2. Число дійсних коренів. 3. Відокремлення дійсних коренів. Метод Штурма. Короткий зміст лекції. Нехай
Тоді всі корені многочлена f(z) знаходяться в середині круга з центром у початку координат і радіусом Якщо f(z) має дійсні корені то вони розміщені в інтервалі Число Метод Ньютона знаходження верхньої межі додатних коренів многочлена з дійсними коефіцієнтами: Число М є верхньою межею додатних коренів многочлена f(z), якщо при x=M многочлен f(x) має додатне значення, а всі його похідні – невід’ємне значення. Якщо Нехай Означення 1. Кількість пар сусідніх чисел цієї послідовності, які мають протилежні знаки, називають кількістю змін знаків даної послідовності. Правило Декарта. Число додатних коренів многочлена з дійсними коефіцієнтами Задача відокремлення дійсних коренів многочлена f(x) полягає в знаходженні тих інтервалів, у кожному з яких лежить тільки один корінь. Метод Штурма відокремлення дійсних коренів многочлена f(x). Нехай f(x) не має кратних коренів. Для многочлена f(x) будуємо ряд Штурма:
Для знаходження многочленів
де Теорема Штурма. Якщо a, b – довільні дійсні числа, які не є коренями многочлена f(x), то число р дійсних коренів многочлена f(x) в інтервалі ]a:b[ дорівнює p=S(a) – S(b), де S(a); S(b) – кількість змін знаків у ряді Штурма відповідно при x=a і x=b. Контрольні питання для самоперевірки. 1. Доведіть, якщо А - найбільший з модулів коефіцієнтів многочлена, не враховуючи 2. Доведіть, якщо при х = а значення многочлена і всіх його похідних додатні, то всі корені многочлена менші а. 3. Що являють собою многочлени Штурма? 4. Доведіть, якщо f(x) – многочлен з дійсними коефіцієнтами, який немає кратних коренів, то а) останній з його многочленів Штурма не залежить від х; б) два сусідніх многочлени Штурма не дорівнюють нулеві при одному і тому ж значенні х; в) якщо один з многочленів Штурма при х=а перетворюється в нуль, то сусідні з ним многочлени Штурма при х=а приймають значення різних знаків; г) якщо один із проміжних множників Штурма перетворюється в нуль, то число змін знаків в ряду Штурма не змінюється; д) при перетворенні в нуль самого многочлена f(х) в ряду його многочленів Штурма загублюється одна змінна знака. 5. Відокремити дійсні корені многочлена Література: [4] § 31;[3]гл.16, §4;[1] §39-41;[12] §15,16;[2]глю6, §4. Лекція 17. Тема: Многочлен над полем раціональних чисел. План. 1. Звідність і незвідність многочленів над полем раціональних чисел. 2. Критерій Ейзенштейна незвідності многочлена з цілими коефіцієнтами. 3. Раціональні корені многочленів з раціональними коефіцієнтами. Короткий зміст лекції. Існують многочлени з раціональними коефіцієнтами довільного степеня, які є незвідними над полем раціональних чисел. Будь–яке алгебраїчне рівняння з раціональними коефіцієнтами множенням на спільний знаменник усіх коефіцієнтів можна звести до рівносильного рівняння з цілими коефіцієнтами. Означення 1. Многочлен р(х) з цілими коефіцієнтами називається примітивним, якщо його коефіцієнти не мають спільних дільників, відмінних від Лема. Добуток двох примітивних многочленів є примітивний многочлен. Теорема 1. Для того, щоб многочлен f(х) з цілими коефіцієнтами був звідним над полем раціональних чисел, необхідно і достатньо, щоб він був звідним над кільцем Z цілих чисел, тобто, щоб існували многочлени Теорема 2 (Ейзенштейна). Якщо в многочлені з цілими коефіцієнтами Теорема 3. В кільці многочленів над полем раціональних чисел існують незвідні многочлени будь–якого степеня. Терема 4. Якщо многочлен 3-го степеня f(х) з раціональними коефіцієнтами немає раціональних коренів, то він є незвідним над полем раціональних чисел. Теорема 5. Якщо Якщо старший коефіцієнт рівняння з цілими коефіцієнтами дорівнює 1, то всі раціональні корені цього рівняння є цілими числами і дільниками вільного члена. Теорема 6. Для того, щоб число Контрольні питання для самоперевірки. 1. Доведіть, якщо р – просте число і n – будь –яке ціле додатне число, то многочлен 2. Доведіть, що многочлен f з цілими коефіцієнтами немає цілих коренів, якщо f (0) і f (1)- непарні числа. 3. Доведіть, що многочлен 4. Розкласти многочлени 5. Доведіть, що многочлен з цілими коефіцієнтами і старшим коефіцієнтом, рівним одиниці, немає дробових коренів. 6. Доведіть, що цілі корені многочлена з цілими коефіцієнтами є дільниками вільного члена. 7. Як знайти всі дільники числа 8. Як знайти всі раціональні корені многочлена з цілими коефіцієнтами? Література: [4], §32;[3],гл.17§1;[1] §56,57,[12] §17,18.
Лекція 18. Тема: Алгебраїчні числа. Розширення полів. План. 1. Мінімальний многочлен алгебраїчного числа. 2. Будова простого алгебраїчного розширення поля. 3. Степінь розширення поля Р. 4. Скінчене розширення поля. 5. Алгебраїчне розширення поля. 6. Простість складеного алгебраїчного розширення. 7. Поле алгебраїчних чисел і його алгебраїчна замкненість. Короткий зміст лекції. Означення 1. Нехай Р [ х ] – кільце многочленів від х над полем Р, де Р – підполе поля F. Елемент Означення 2. Число називається алгебраїчним, якщо воно є коренем будь-якого многочлена з раціональними коефіцієнтами. Означення 3. Нормований многочлен Означення 4.Мінімальним полем Р(М), яке містить числову множину М, називається поле, яке є перетином всіх числових полів, які містять множину М. Означення 5. Мінімальне розширення поля?, яке містить число Означення 6. Поле?( Теорема 1. Поле?(
складається з усіх чисел вигляду,
де Якщо
причому Означення 7. Розширення
Система елементів Отже, розширення Означення 8. Розмірність скінченого розширення Степінь скінченого розширення Теорема 2. Просте алгебраїчне розширення?( Означення 9. Розширення Означення 10. Розширення Теорема 3. Будь–яке скінчене розширення поля? є його алгебраїчним та складеним розширенням. Теорема 4. Кожне складене алгебраїчне розширення поля? є простим розширенням цього поля. Терема 5. Множина А всіх алгебраїчних чисел замкнена в кінці С комплексних чисел. Терема 6. Поле алгебраїчних чисел алгебраїчно замкнене. Контрольні питання для самоперевірки. 1. Дайте озна
|
||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 664; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.155.253 (0.009 с.) |

 ) містить деякий член
) містить деякий член  , то він містить і член, утворений з даного перестановкою показників k 1+ k 2+…+ kn.
, то він містить і член, утворений з даного перестановкою показників k 1+ k 2+…+ kn.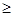 k 2
k 2 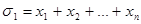 ;
; ;
;
 цих змінних з коефіцієнтами того самого поля Р. Таке зображення є єдиним.
цих змінних з коефіцієнтами того самого поля Р. Таке зображення є єдиним. n.
n.
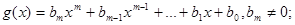
 ,
, ,
,  ,...,
,...,  - корені многочлена
- корені многочлена  .
.

 =
= 
 …
… 
 0 … 0
0 … 0 …
… 
 рядків
рядків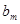
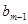 0..
0.. 
 0 … 0
0 … 0 рядків
рядків .
.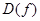 многочлена
многочлена  називається елемент поля Р
називається елемент поля Р ,
, - результант многочлена
- результант многочлена  .
.
 і
і  за спадними степенями одного із змінних, наприклад x;
за спадними степенями одного із змінних, наприклад x; як параметр;
як параметр; ;
; , гл.15, § 3,
, гл.15, § 3,  , гл. 6, § 27.
, гл. 6, § 27. ,...,
,...,  над полем P при
над полем P при 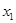 =
=  =
=  =
=  , утворене з числового поля P приєднанням кореня
, утворене з числового поля P приєднанням кореня  , незвідного у полі P многочлена n -го степеня
, незвідного у полі P многочлена n -го степеня  , складається з усіх чисел виду
, складається з усіх чисел виду  , де
, де  ,
,  ,...,
,...,  - будь-які числа з поля P.
- будь-які числа з поля P. - корінь незвідного над полем P многочлена
- корінь незвідного над полем P многочлена 
 . Позбавимося від ірраціональності в знаменнику дробу
. Позбавимося від ірраціональності в знаменнику дробу  , де
, де 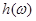 над тим же полем P:
над тим же полем P: , (*)
, (*) і
і  - многочлени над P.
- многочлени над P. із (*) одержуємо (при умові, що
із (*) одержуємо (при умові, що  =0).
=0).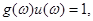

 .
. то із рівності
то із рівності 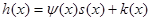 , де степінь k(x)<n, при
, де степінь k(x)<n, при 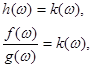
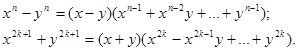

 , § 23
, § 23 , то існує розширення К поля Р, в якому міститься деякий корінь многочлена f(x).
, то існує розширення К поля Р, в якому міститься деякий корінь многочлена f(x). степеня
степеня  існує таке розширення L поля Р, що f(x) можна подати в
існує таке розширення L поля Р, що f(x) можна подати в  у вигляді добутку лінійних многочленів.
у вигляді добутку лінійних многочленів. розкладається на лінійні множники.
розкладається на лінійні множники. з дійсними коефіцієнтами має хоч би один комплексний корінь.
з дійсними коефіцієнтами має хоч би один комплексний корінь. де
де  ,
,  ,...,
,...,  - корені,
- корені, 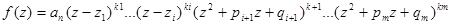

 перетворюємо це рівняння до вигляду:
перетворюємо це рівняння до вигляду:
 . Достатньо вміти розв’язувати кубічне рівняння
. Достатньо вміти розв’язувати кубічне рівняння  . (*)
. (*) , тоді одержуємо рівняння:
, тоді одержуємо рівняння:
 і
і  додаткову умову:
додаткову умову: 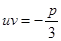 , одержуємо рівняння:
, одержуємо рівняння: 


 ;
;
 ;
; - дискримінант кубічного рівняння (*).
- дискримінант кубічного рівняння (*).
 - формула Кардано для знаходження коренів кубічного рівняння.
- формула Кардано для знаходження коренів кубічного рівняння.
 :
: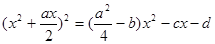 .
. , де t- допоміжне невідоме:
, де t- допоміжне невідоме: .
. .Для цього треба виконання умов:
.Для цього треба виконання умов: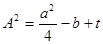 ;
;  ;
; 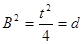 .
. ,
, - будь-який корінь останнього рівняння, то одержуємо сукупність рівнянь:
- будь-який корінь останнього рівняння, то одержуємо сукупність рівнянь: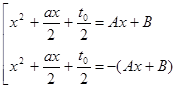


 , § 23, 24;
, § 23, 24; 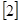 , гл.6, § 3.
, гл.6, § 3. - многочлен з комплексними коефіцієнтами;
- многочлен з комплексними коефіцієнтами;
 .
.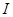 -
-  і
і  - верхні межі відповідно додатних коренів многочленів з дійсними коефіцієнтами f(x),
- верхні межі відповідно додатних коренів многочленів з дійсними коефіцієнтами f(x),  , то додатні корені многочлена f(x) знаходяться в проміжку
, то додатні корені многочлена f(x) знаходяться в проміжку  , а від’ємні – в проміжку
, а від’ємні – в проміжку 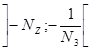
 - деяка впорядкована послідовність дійсних чисел.
- деяка впорядкована послідовність дійсних чисел. дорівнює або на парне число менше кількості змін знаків у послідовності його коефіцієнтів.
дорівнює або на парне число менше кількості змін знаків у послідовності його коефіцієнтів.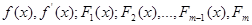 .
. , застосовуємо алгоритм аналогічний алгоритму Евкліда:
, застосовуємо алгоритм аналогічний алгоритму Евкліда:
 =-
=- 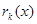 , тобто всі остачі беруться з протилежним знаком.
, тобто всі остачі беруться з протилежним знаком. ;
;
 1.
1. і
і  ненульового степеня з цілими коефіцієнтами такі, що
ненульового степеня з цілими коефіцієнтами такі, що 
 діляться на деяке просте число р, причому
діляться на деяке просте число р, причому  не ділиться на р
не ділиться на р  , а старший коефіцієнт
, а старший коефіцієнт  , де p і q – взаємно прості числа, є коренем рівняння
, де p і q – взаємно прості числа, є коренем рівняння  = 0 з цілими коефіцієнтами, то
= 0 з цілими коефіцієнтами, то 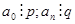 .
.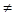 0).
0). незвідний в кільці Q [ x ].
незвідний в кільці Q [ x ]. , де р- просте число є незвідним над полем раціональних чисел.
, де р- просте число є незвідним над полем раціональних чисел. і
і 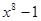 на незвідні множники над полем раціональних чисел.
на незвідні множники над полем раціональних чисел.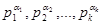 , де
, де 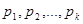 - різні прості числа.
- різні прості числа.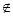 ?, називають розширенням поля?, утвореного приєднанням числа
?, називають розширенням поля?, утвореного приєднанням числа  ,
, - довільні числа із поля?.
- довільні числа із поля?. ,
, поля? називається скінченим, якщо в полі
поля? називається скінченим, якщо в полі  , що будь – який елемент
, що будь – який елемент  є
є  .
.


