
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: Многочлени від однієї змінної.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
План. 1. Кільце многочленів від однієї змінної. 2. Відношення подільності в кільці многочленів. 3. Ділення з остачею. Ідеали кільця многочленів. 4. Теорема Безу. 5. Найбільший спільний дільник двох многочленів. Алгоритм Евкліда. 6. Найменше спільне кратне двох многочленів. 7. Звідні та незвідні многочлени над полем. Короткий зміст лекції: Нехай K – довільна область цілісності з одиницею і R – її підкільце з одиницею. Означення 1. Елемент х Елемент, який не є алгебраїчним над R, називається трансцендентним над R. Означення 2. Мінімальне розширення кільця R, яке містить трансцендентний над R елемент х, називається простим трансцендентним розширенням кільця R, або кільцем многочленів від однієї змінної над R, позначається через R [ x ]. Елементи цього кільця називають многочленами від х над R, позначають символами f(x), g(x) і т. д. Нуль кільця R [ x ] називають нульовим многочленом або нуль-многочленом. Будь-який ненульовий многочлен f(x) можна подати у вигляді: f(x) = anxn+an-1xn-1+…+a1x+a0; ai Кільце многочленів R [ x ] є областю цілісності. Алгебраїчна рівність многочленів: Два многочлени з кільця R [ x ] рівні тоді і тільки тоді, коли вони мають однакові степені і попарно рівні відповідні коефіцієнти. Кожен многочлен f(x) з кільця R [ x ] визначає відображення Функціональна рівність многочленів: Якщо область цілісності R має характеристику 0, то многочлени f(x), g(x) Алгебраїчне і функціональне тлумачення многочленів рівносильні над областю цілісності характеристики 0. Нехай Р – поле. Означення 3. Многочлен f(x) Означення 4. Многочлен f(x) Теорема (про ділення з остачею). Довільний многочлен f(x) Кільце P [ x ] многочленів над полем Р є кільцем головних ідеалів. Кільце многочленів Р [ x ] над полем Р є евклідовим. Теорема Безу. Для будь-якого елемента Означення 5. Якщо многочлен d(x) – дільник многочленів f(x) і g(x), то він називається спільним дільником цих многочленів. Означення 6. Спільний дільник многочленів f(x) і g(x), який ділиться на будь-який спільний дільник цих многочленів, називається найбільшим спільним дільником (НСД) многочленів f(x) і g(x), позначається (f, g). Для знаходження НСД f і g застосовується алгоритм ділення з остачею (алгоритм Евкліда): F = g G = r1 ………… rk-2 = rk-1 rk-1 = rk rk Означення 7.Спільним кратним многочленів f, g Означення 8.Найменшим спільним кратним многочленів f і g називається спільне кратне f і g, яке ділить будь-яке спільне кратне цих многочленів, позначається НСК або [ f, g ]. Для будь-яких многочленів f і g
Означення 9. Многочлен f(x) Означення 10. Многочлен f(x) Контрольні запитання для самоперевірки. 1. Довести, що многочлени від однієї змінної з коефіцієнтами з будь-якого поля Р утворюють кільце. 2. Перерахувати найпростіші властивості подільності многочленів. 3. Доведіть теорему про ділення з остачею. 4. Дайте означення найбільшого спільного дільника двох многочленів. 5. В чому суть алгоритму Евкліда для многочленів? 6. Доведіть, що НСД двох многочленів над полем Р є многочлен над полем Р, що визначається з точністю до множника нульового степеня. 7. Доведіть, якщо d(x) – НСД многочленів f(x) і g(x) над полем Р, то існують многочлени d(x) = f(x) 1. Як знайти НСД трьох многочленів? 2. Які многочлени називаються взаємно простими? 3. Який многочлен називається незвідним над полем Р? 4. Доведіть, якщо незвідний многочлен р(х) ділиться на многочлен q(x) ненульового степеня, то p(x) = c 5. Доведіть, якщо р(х) – незвідний многочлен, f(x) – будь-який многочлен над полем Р, то або f(x) ділиться на р(х), або многочлени f(x) і р(х) взаємно прості. 6. Доведіть, якщо добуток f(x) 7. Доведіть, що кільце многочленів Р [ x ] є кільце головних ідеалів. Література: [4], гл.V, 21,22; [1], гл. 10, 47; [3], гл. 14, 1,2. Лекція 10. Тема: Корені многочлена. План. 1. Ділення многочлена на двочлен х-а. Схема Горнера. 2. Корені многочлена. Кратні корені. 3. Похідна многочлена. 4. Теорема про кратні множники многочлена. 5. Теорема про спряжені корені. 6. Відокремлення кратних множників многочлена.
Короткий зміст лекції. Схема Горнера ділення многочлена f(x) на двочлен х-а. Нехай f(x) = anxn+an-1xn-1+…+a1x+a0. g(x) = x-a. За теоремою про ділення з остачею маємо: (*) f(x) = (x-a) Q(x) = bn-1xn-1+bn-2xn-2+…+b1x+b0. Рівність (*) запишемо у вигляді таблиці,
яка називається схемою Горнера ділення многочлена f(x) на двочлен х-а. Означення 1. Число Означення 2. Число Означення 3.Похідною многочлена f(x) = anxn+an-1xn-1+…+a1x+a0 називають многочлен f’(x) = nanxn-1+(n- 1 )an-1xn-2+…+ 2 a2x+a1. Похідна многочлена нульового степеня і нуль-многочлена дорівнює нулю. Якщо поле Р має характеристику нуль, то для кожного многочлена f(x) Означення 4. Елемент Означення 1) і 4) рівносильні. Для того, щоб елемент а f(a) = f’(a) = … =fk-1(a); f(k)(a) Якщо а Многочлен f(x) має корінь кратності k >1 тоді і тільки тоді, коли (f, f’) = 1. Теорема про спряжені корені многочлена. Якщо комплексне число Відокремлення кратних множників: Кожний многочлен f над полем Р можна представити у вигляді
де Фi – добуток тих многочленів, кратність яких в f дорівнює i. Якщо f кратних множників немає, то F = Ф1,
де Знаходимо НСД многочленів f і f’: d 1 = d (f, f’) = Знаходимо Одержуємо рівності:
d1 = d2 = ……………. dm-2 = dm-1 = dm = 1 Для знаходження Фi i = 1,2,3,…, m побудуємо многочлени: Q1 = Q2 = Q3 = …………… qm-1 = qm = звідси,
Теорема. Будь-який многочлен f(x) степеня n над полем комплексних чисел С має n коренів з урахуванням їх кратності. Контрольні питання для самоперевірки. 1. Які задачі можна розв’язувати, застосовуючи схему Горнера? 2. Що називається коренем многочлена? 3. Доведіть, що х = а тоді і тільки тоді є коренем многочлена f(x), якщо f(x) ділиться на (х-а). 4. Вивести формулу Тейлора для мночлена над будь-яким полем Р. 5. Як використовується схема Горнера для розкладу многочлена за формулою Тейлора? 6. Який корінь многочлена називається кратним? 7. Як визначається кратність кореня? 8. Як відокремити кратні корені многочлена? 9. Яку найбільшу кількість коренів може мати многочлен n -го степеня? Література: [4], гл. V, 23; [1], гл. 10, 49; [10], гл. 3, 1.1; 1.2; [2], гл. 6, 1.
Лекція 11.
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 1061; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.44.145 (0.009 с.) |

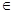 K називається алгебраїчним над кільцем R, якщо в R існують такі елементи a0, a1, …, an, які не всі дорівнюють 0, що anxn+an-1xn-1+…+a1x+a0 = 0.
K називається алгебраїчним над кільцем R, якщо в R існують такі елементи a0, a1, …, an, які не всі дорівнюють 0, що anxn+an-1xn-1+…+a1x+a0 = 0.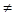 0.
0.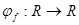 таке, що
таке, що 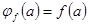 .
.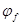 і
і 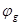 , які вони визначають.
, які вони визначають.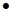 s(x), позначається f(x)
s(x), позначається f(x) 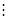 g(x), або g(x)/f(x).
g(x), або g(x)/f(x).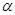 з поля Р остача при діленні многочлена f(x)
з поля Р остача при діленні многочлена f(x) 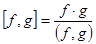 .
.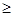 1 і існують такі многочлени g, s
1 і існують такі многочлени g, s 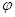 (х) і
(х) і  (х) над тим же полем, що
(х) над тим же полем, що
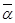 .
.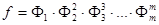 ,
,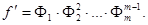
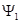 ;
;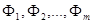 .
.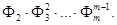

 і т. д.
і т. д.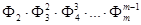 ;
;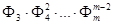
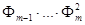
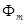
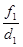 =
= 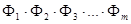 ,
,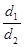 =
= 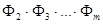 ,
,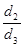 =
= 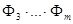 ,
,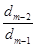 =
=  ,
,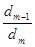 =
= 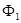 =
= 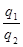 ;
; 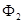 =
= 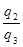 ;...;
;...; 


