
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розділ I. Многочлени від однієї змінноїСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Розділ I. Многочлени від однієї змінної § 1. Кільце многочленів. Алгебраїчна і функціональна рівність многочленів. Відношення подільності в кільці многочленів.
Питання для самоконтролю:
1) Многочлен – це … 2) Старший коефіцієнт многочлена – це …, 3) Чи є такий запис многочлена його канонічною формою. Відповідь пояснити. 4) Канонічне представлення многочлена єдине чи ні? 5) Чому рівний степінь суми та добутку многочлена? 6) Що означають записи 7) В чому полягає функціональна рівність многочленів? 8) Яка умова алгебраїчної рівності многочленів? 9) Чи вірно, що коли многочлени рівні між собою функціонально, то вони рівні і алгебраїчно? 10) Асоційовані многочлени – це … 11) Що означає запис: Задачі
1) Знайти канонічну форму многочлена: а) б) 2) Виконати ділення з остачею („кутом”): 3) Використовуючи схему Горнера поділити в кільці 4) При якій умові многочлен 5) При яких значеннях 6) Довести, що з функціональної точки зору ці многочлени рівні:
7) Знайти всі значення деякого многочлена 8) Знайти суму коефіцієнтів многочленна 9) Знайти необхідну і достатню умову подільності многочленів 10) Знайти остачу від ділення 11) При діленні многочлена 12) При діленні многочлена 13) При діленні многочлена
§ 2. Ділення многочлена на двочлен (x-a). Теорема Безу. Схема Горнера. Розклад многочлена за степенями (x-a). Найбільший спільний дільник і найменше спільне кратне многочленів.
Питання для самоконтролю:
1) Сформулювати теорему Безу і наслідок з неї. 2) Що означає розкласти многочлен за степенями 3) Який дільник є спільним для многочленів? 4) Спільний дільник називається найбільшим спільним дільником многочленів, якщо… 5) Взаємно прості многочлени – це… 8) Що означає лінійно представити найбільший спільний 9) При якій умові 10) Алгоритм Евкліда. Для чого його використовують? 11) Спільне кратне многочленів 12) Що називається НСК многочленів і як його обчислити?
Задачі
1) Знайти частку і остачу від ділення многочлена 2) Знайти значення многочлена а) б) 3) Методом невизначених коефіцієнтів знайти частку і остачу від ділення 4) Остачі від ділення многочлена 5) При діленні многочлена 6) Знайти остачу від ділення многочлена 7) Користуючись схемою Горнера розкласти многочлен а) б) в) 8) Довести, що многочлен а) на 9) Користуючись алгоритмом Евкліда, знайти найбільший спільний дільник таких многочленів: а) 10) Знайти найменше спільне кратне таких многочленів: 11) Визначити многочлени а)
Задачі
1) Встановити чи звідні над полем Q такі многочлени: 2) Розкласти на незвідні множники многочлен 3) Розкласти на незвідні у полі Р множники такі многочлени: 4) Знайти многочлен шостого степеня 5) Розкласти многочлен f(x) за степенями двочлена
6) Знайти кратність 7) При яких значеннях 8) Визначити коефіцієнт 9) Відокремити кратні множники таких многочленів: 10) Визначити коефіцієнт 11) Знайти многочлен третього степеня, якщо його корені рівні Задачі
1) Довести тотожність: 2) Використовуючи інтерполяційну формулу Ньютона, побудувати многочлен найменшого степеня
а)
б)
3) Знайти многочлен найменшого степеня
а) Обчислити
б) Обчислити
4) Знайти цілі числа а) б) 5) У полі 6) Перевірити, чи є раціональні дроби 7) Розкласти дріб на елементарні дроби: 8) Розкласти дріб на елементарні дроби: 9) Розкласти дріб на елементарні дроби в полі комплексних чисел: 10) Розкласти дріб на елементарні дроби в полі раціональних чисел:
Задачі
1) Знайти канонічну форму таких многочленів: 2) Упорядкувати лексикографічно і знайти вищий член многочлена:
3) Застосовуючи заміну 4) Розкласти на незвідні множники многочлен 5) Чи є симетричними такі многочлени: 6) Виразити через елементарні симетричні многочлени: 7) Перевірити вірність даної рівності: 8) Виразити через елементарні симетричні многочлени: Задачі 1) У множині дійсних чисел розв’язати системи: 2) Розв’язати систему ірраціональних рівнянь: 3) Розв’язати системи рівнянь, звівши їх за допомогою допоміжних змінних до симетричних многочленів: 4) Розв’язати такі рівняння: 5) Скоротити дріб 6) Скласти квадратне рівняння, коренями якого є куби коренів рівняння 7) Скласти квадратне рівняння, коренями якого є 8) Знайти многочлен третього степеня, коренями якого є: 9) Знайти многочлен четвертого степеня, коренями якого є: 10) Довести такі тотожності: 11) Довести, що коли 12) Розкласти на незвідні над полем R множники симетричний однорідний многочлен
Задачі
1) Обчислити результант многочленів: 2) При якому значенні
3) Обчислити дискримінант многочленів: 4) Довести, що дискримінант многочлена 5) При якому значенні 6) Розв’язати системи рівнянь:
Задачі
1) Знайти многочлен найменшого степеня, в якого: 2) Знайти многочлен найменшого степеня з дійсними коефіцієнтами, якщо 3) Знайти суму квадратів коренів многочлена 5) Сума двох коренів рівняння 6) Використовуючи формули Вієта, побудувати многочлен за його коренями:
7) Знайти зведений многочлен, в якого корені задовольняють умову: 8) Корені многочлена 9) Чи утворюють корені рівняння 10) Визначте
Задачі
1) Розв’язати рівняння:
2) Знайти нормований многочлен найменшого степеня з дійсними коефіцієнтами, що має: а) простий корінь b) простий корінь с) трикратний корінь 3) Знаючи, що число
4) Розкласти многочлен
5) Яким умовам повинні задовольняти дійсні коефіцієнти многочлена:
Рівняння третього степеня Питання для самоконтролю: 1) Яке рівняння називається рівнянням третього степеня? 2) Рівняння 3) Як називається вираз 4) Як знайти корені рівняння 5) Коли рівняння 6) Якщо 7) Рівняння 8) U1 i V1 – це … 9) З якої умови знаходиться числа U1 i V1?
Задачі
1) Звести кубічне рівняння до виду, у якому відсутній доданок з невідомим у другому степені:
2) Розв’язати рівняння:
3) При яких дійсних значеннях 4) Які корені залежно від значення числа 5) Розв’язати рівняння 6) Розв’язати рівняння 7) Розв’язати кубічне рівняння
§ 11. Відокремлення дійсних коренів многочленів.
Питання для самоконтролю: 1) Як розташовані комплексні корені з дійсними коефіцієнтами відносно дійсної осі? 2) Де розміщені всі дійсні корені рівняння 3) Число М є верхньою межею додатних коренів многочлена 4) Кількість змін знаків деякої впорядкованої послідовності дійсних чисел 5) Сформулюйте правило Декарта. 6) Яка заміна використовується для знаходження кількості від’ємних коренів многочлена 7) Щоб побудувати ряд Штурма необхідно… 8) Сформулювати теорему Штурма. 9) Чи мають дві сусідні функції ряду Штурма спільні корені? 10) Якщо 11) Якщо 12) Якщо
Задачі
1) Знайти верхню межу дійсних коренів многочлена методом Ньютона:
2) Знайти нижню межу дійсних коренів многочлена методом Ньютона:
3) Обмежити зверху і знизу дійсні корені многочленів:
4) Знайти число дійсних коренів для многочленів: 5) Відокремити дійсні корені многочленів: 6) Оцінити за правилом Декарта число додатніх і від’ємних коренів многочлена
Задачі
1) Розв’язати рівняння: 2) Знайти раціональні корені рівняння: 3) Розкласти на незвідні множники дані многочлени або довести їх незвідність: 4) Дослідити на звідність у полі Q такий многочлен: 5) Що можна сказати про звідність даного многочлена у
6) Користуючись критерієм Ейзенштейна, довести незвідність над полем Q многочленів:
Задачі
1) Довести, що число a є алгебраїчним і знайти його мінімальний многочлен:
2) Довести, що числа 3) Довести безпосередньо, що число
4) Для даного числа
5) Чи міститься в полі 6) Знайти алгебраїчне число, приєднанням якого до Q поля можна дістати складне алгебраїчне розширення:
7) Нехай 8) Знайти вираження для кожного з чисел
Задачі
1) Позбавитися від ірраціональності в знаменнику дробу:
2) Позбавитися від ірраціональності в знаменнику дробу: 3) Позбавитися від ірраціональності в знаменнику дробу: 4) Позбавитися від ірраціональності в знаменнику дробу: 5) В полі 6) Звільнитись від 7) Спростити вираз: ТЕМАТИЧНІ ТЕСТИ ТЕСТ 1
Подільність. Взаємнопрості многочлени.
1) Чи є многочленом від змінної а) б) в) г) 2) Який степінь має многочлен а) 3; б) 4; в) 8; г) 7. 3) Канонічною формою многочлена а) коли його члени впорядковані в довільному порядку; б) коли його члени впорядковані за спаданням степеня в) коли його члени впорядковані за зростанням степеня г) коли його члени впорядковані за спаданням значення 4) Які з многочленів записані в канонічній формі: а) б) в) г) 5) Допишіть нерівність: а) б) в) г) 6) При яких а) б) в) г) 7) У кільці а) незвідні; б) асоційовані; в) подібні; г) звідні. 8) Знайти суму коефіцієнтів многочлена а) -5; б) 24; в) 0; г) -25. 9) Як називається многочлен а) ділене; б) частка; в) остача; г) дільник. 10) Як називається вираз виду а) лінійний запис НСД; б) лінійний запис НСК; в) лінійне представлення НСД; г) лінійне представлення НСК. 11) … називається будь-який многочлен а) СД; б) НСК; в) НСД; г) СК. 12) Якщо а) СД; б) НСК; в) НСД; г) СК. 13) Многочлен а) незвідним; б) асоційованим; в) симетричним; г) звідним. 14) Чи вірне твердження: многочлен першого степеня над будь-яким полем а) так; б) ні; в) в окремих випадках; г) можливо. 15) Поле а) канонічним полем; б) полем розкладу; в) кратним полем; г) звідним полем. 16) Якщо а) асоційованими; б) звідними; в) незвідними; г) взаємно простими. 17) Число всіх можливих коренів многочлена а) дорівнює б) не перевищує в) більше г) менше 18) Скільки многочленів можуть бути найменшим спільним дільником многочленів а) 2; б) 1; в) 4; г) безліч. 19) Скільки многочленів можуть бути найменшим спільним кратним многочленів | ||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

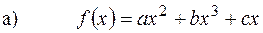


 і
і 

 в кільці
в кільці  ;
;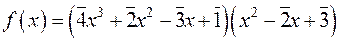 у кільці
у кільці  .
. на многочлен
на многочлен 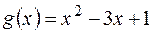 ;
;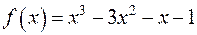 на многочлен
на многочлен  .
. многочлен
многочлен  на лінійний двочлен
на лінійний двочлен  :
: ;
; .
. ділиться на многочлен
ділиться на многочлен  .
. многочлени
многочлени  і
і  з кільця
з кільця  рівні між собою:
рівні між собою:  .
. з кільця
з кільця  .
. при яких многочлен
при яких многочлен  . Записати
. Записати  .
. в кільці
в кільці  на
на  в кільці
в кільці 
 в кільці
в кільці  . Знайти остачу від ділення
. Знайти остачу від ділення  на
на  .
. дістали остачу 3, а при діленні
дістали остачу 3, а при діленні  на
на  - остачу 9. Яка буде остача, якщо
- остачу 9. Яка буде остача, якщо  ?
? у кільці
у кільці  дістали частку
дістали частку  та остачу
та остачу  . Знайти остачу від ділення
. Знайти остачу від ділення  .
. ?
? на многочлен
на многочлен  .
. в точці
в точці  , якщо:
, якщо: К = С;
К = С; ;
; ;
;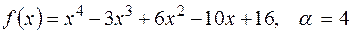 .
.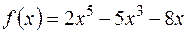 на
на  .
. відповідно дорівнюють
відповідно дорівнюють  . Знайти остачу від ділення цього многочлена на
. Знайти остачу від ділення цього многочлена на  .
.
 отримали остачі 5, -4, 6 відповідно. Знайдіть остачу при діленні многочлена
отримали остачі 5, -4, 6 відповідно. Знайдіть остачу при діленні многочлена  .
. на двочлени:
на двочлени:

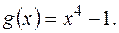
 , якщо
, якщо ;
; ;
; .
. ділиться:
ділиться: над областю цілісності К з одиницею;
над областю цілісності К з одиницею; в кільці
в кільці  .
. ;
; ;
;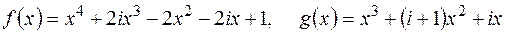 .
. ;
; ;
; і
і  так, щоб для многочленів
так, щоб для многочленів  , якщо
, якщо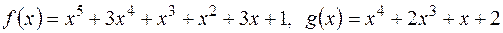 ;
; .
.
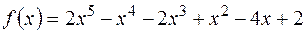 в полях Q, R, C, якщо він має дві пари коренів у полі, які є протилежними числами.
в полях Q, R, C, якщо він має дві пари коренів у полі, які є протилежними числами.
 , якщо
, якщо 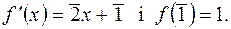
 і знайти
і знайти  , якщо:
, якщо: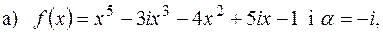
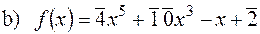 належить
належить  .
. кореня
кореня  многочлена
многочлена 
 многочлен
многочлен  має кратний корінь:
має кратний корінь: 
 так, щоб многочлен
так, щоб многочлен  мав число -1 коренем не нижче другої кратності.
мав число -1 коренем не нижче другої кратності.
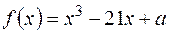 був рівним подвійному другому.
був рівним подвійному другому. , де
, де  - корені многочлена
- корені многочлена  .
.
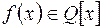 за такою таблицею:
за такою таблицею:






 такі, що
такі, що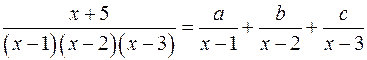 ;
; .
. знайти нескоротний дріб, який дорівнює
знайти нескоротний дріб, який дорівнює 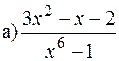 ,
,  .
. елементарними над полем
елементарними над полем 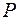 , якщо:
, якщо:






 з кільця
з кільця  .
. розкласти на незвідні у полі
розкласти на незвідні у полі  , якщо
, якщо 
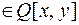 :
:


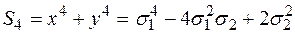 .
.
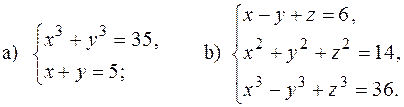





 , якщо відомо, що
, якщо відомо, що 




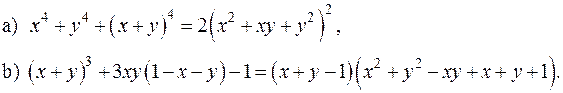
 , то
, то 




 дорівнює дискримінанту многочлена
дорівнює дискримінанту многочлена 

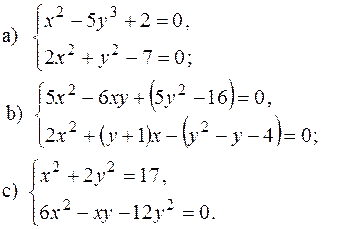
 – прості;
– прості; – його потрійний корінь.
– його потрійний корінь.
 дорівнює 1. Визначити
дорівнює 1. Визначити 
 , а
, а  ,
,  ,
,  є коренями многочлена
є коренями многочлена  .
. .
. арифметичну прогресію?
арифметичну прогресію? , якщо
, якщо  ;
; , якщо
, якщо  ;
; , якщо
, якщо  .
.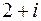 і двократний корінь 1;
і двократний корінь 1; і двократні корені
і двократні корені  та
та  ;
;

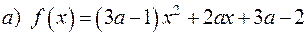 , щоб він мав два різних дійсних корені;
, щоб він мав два різних дійсних корені; , щоб він мав один дійсний корінь.
, щоб він мав один дійсний корінь. третього степеня зводиться до рівняння виду
третього степеня зводиться до рівняння виду  за допомогою …
за допомогою … ?
? , то які корені має рівняння
, то які корені має рівняння 


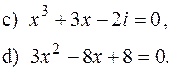
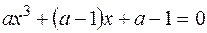 має кратний корінь? Знайти його.
має кратний корінь? Знайти його. ?
? , коли відомо, що серед його коренів є два числа, обернених за абсолютною величиною і протилежних за знаком.
, коли відомо, що серед його коренів є два числа, обернених за абсолютною величиною і протилежних за знаком. , коли відомо, що добуток двох його коренів дорівнює 1.
, коли відомо, що добуток двох його коренів дорівнює 1. , коли відомо, що його коефіцієнти в порядку спадання степенів утворюють геометричну прогресію з знаменником 2.
, коли відомо, що його коефіцієнти в порядку спадання степенів утворюють геометричну прогресію з знаменником 2. ?
? – це …
– це …


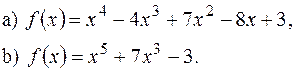
 на проміжку [0,2],
на проміжку [0,2],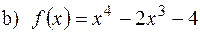 на проміжку [-3,5].
на проміжку [-3,5].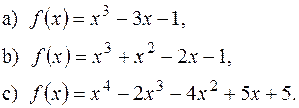

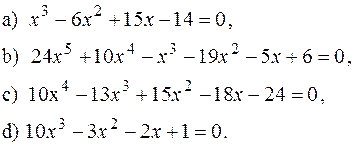



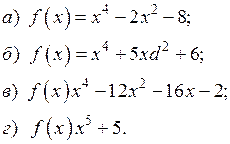


 і
і  алгебраїчні. Знайти степінь числа
алгебраїчні. Знайти степінь числа  .
.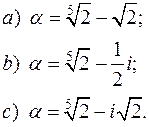

 число
число  ? В полі
? В полі 
 ?
?
 де
де 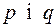 - прості числа,
- прості числа, ,
, .
. і
і  - натуральні числа, причому
- натуральні числа, причому  і
і  - не цілі. Довести, що
- не цілі. Довести, що 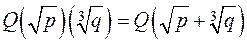 .
.
 де
де  ,
, де
де 



 , де
, де  , знайти представлення для числа
, знайти представлення для числа  у вигляді
у вигляді  .
. , якщо
, якщо 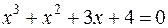 .
.
 вираз:
вираз: ;
; ;
; ;
; .
. :
: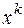 ;
; над полем
над полем  ;
; над полем
над полем  ;
; над кільцем
над кільцем  ;
; над полем
над полем  .
. …
… ;
;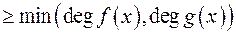 ;
; ;
; .
. та
та  многочлен з кільця
многочлен з кільця  та
та 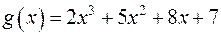
 ;
; ;
; ;
; .
. многочлени
многочлени  з кільця
з кільця  у виразі
у виразі  :
: :
: такий, що
такий, що :
: , то
, то  називається …
називається … називається … у полі
називається … у полі  і в кільці
і в кільці  ,
,  і
і  .
. , де многочлен
, де многочлен  , то многочлени
, то многочлени  над
над  :
:


