
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розділ IV. Многочлени над полем раціональних чисел та алгебраїчні числаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Цілі і раціональні корені многочлена з цілими коефіцієнтами. Критерій незвідності Ейзенштейна Питання для самоконтролю: 1) Число якого виду може бути раціональним коренем многочлена? 2) При якій умові число 3) Коли всі раціональні корені є цілими числами і являються дільниками вільного члена? 4) Якщо числа 5) Умова звідності многочлена 6) Якщо многочлен 7) Сформулюйте критерій Ейзенштейна незвідності многочлена з цілими коефіцієнтами. Задачі
1) Розв’язати рівняння: 2) Знайти раціональні корені рівняння: 3) Розкласти на незвідні множники дані многочлени або довести їх незвідність: 4) Дослідити на звідність у полі Q такий многочлен: 5) Що можна сказати про звідність даного многочлена у
6) Користуючись критерієм Ейзенштейна, довести незвідність над полем Q многочленів:
Алгебраїчні і трансцендентні числа. Будова простого алгебраїчного розширення поля Питання для самоконтролю: 1) Яке число називається алгебраїчним відносно поля 2) Чи існує незвідний зведений многочлен 3) Яке поле називається простим алгебраїчним (трансцендентним) розширенням поля 4) З яких чисел складається поле 5) З яких чисел складається просте алгебраїчне розширення Р(α) поля 6) Яке розширення поля 7) Розширення 8) Яка степінь будь-якого квадратичного розширення? 9) Яке розширення 10) Якщо всі елементи поля
Задачі
1) Довести, що число a є алгебраїчним і знайти його мінімальний многочлен:
2) Довести, що числа 3) Довести безпосередньо, що число
4) Для даного числа
5) Чи міститься в полі 6) Знайти алгебраїчне число, приєднанням якого до Q поля можна дістати складне алгебраїчне розширення:
7) Нехай 8) Знайти вираження для кожного з чисел
Позбавлення від алгебраїчної ірраціональності в знаменнику дробу
Питання для самоконтролю:
1) На яких фактах ґрунтуються основні методи розв’язування задач на позбавлення від ірраціональності в знаменнику дробу? 2) Що треба зробити, щоб позбавиться від ірраціональності в знаменнику дробу Задачі
1) Позбавитися від ірраціональності в знаменнику дробу:
2) Позбавитися від ірраціональності в знаменнику дробу: 3) Позбавитися від ірраціональності в знаменнику дробу: 4) Позбавитися від ірраціональності в знаменнику дробу: 5) В полі 6) Звільнитись від 7) Спростити вираз: ТЕМАТИЧНІ ТЕСТИ ТЕСТ 1
Подільність. Взаємнопрості многочлени.
1) Чи є многочленом від змінної а) б) в) г) 2) Який степінь має многочлен а) 3; б) 4; в) 8; г) 7. 3) Канонічною формою многочлена а) коли його члени впорядковані в довільному порядку; б) коли його члени впорядковані за спаданням степеня в) коли його члени впорядковані за зростанням степеня г) коли його члени впорядковані за спаданням значення 4) Які з многочленів записані в канонічній формі: а) б) в) г) 5) Допишіть нерівність: а) б) в) г) 6) При яких а) б) в) г) 7) У кільці а) незвідні; б) асоційовані; в) подібні; г) звідні. 8) Знайти суму коефіцієнтів многочлена а) -5; б) 24; в) 0; г) -25. 9) Як називається многочлен а) ділене; б) частка; в) остача; г) дільник. 10) Як називається вираз виду а) лінійний запис НСД; б) лінійний запис НСК; в) лінійне представлення НСД; г) лінійне представлення НСК. 11) … називається будь-який многочлен а) СД; б) НСК; в) НСД; г) СК. 12) Якщо а) СД; б) НСК; в) НСД; г) СК. 13) Многочлен а) незвідним; б) асоційованим; в) симетричним; г) звідним. 14) Чи вірне твердження: многочлен першого степеня над будь-яким полем а) так; б) ні; в) в окремих випадках; г) можливо. 15) Поле а) канонічним полем; б) полем розкладу; в) кратним полем; г) звідним полем. 16) Якщо а) асоційованими; б) звідними; в) незвідними; г) взаємно простими. 17) Число всіх можливих коренів многочлена а) дорівнює б) не перевищує в) більше г) менше 18) Скільки многочленів можуть бути найменшим спільним дільником многочленів а) 2; б) 1; в) 4; г) безліч. 19) Скільки многочленів можуть бути найменшим спільним кратним многочленів а) 2; б) 1; в) 4; г) безліч. 20) Раціональний дріб а) б) в) г) 21) а) СД; б) СК; в) НСК; г) НСД. 22) Як називається вираз а) канонічний розклад многочлена б) розклад многочлена в) лінійне представлення многочлена г) розклад многочлена 23) Елементарним дробом у полі а) б) в) г) 24) Який з раціональних дробів є елементарним над полем а) б) в) г) 25) Неправильний дріб а) суму многочлена і неправильного дробу; б) різницю многочлена і правильного дробу; в) суму многочлена і правильного дробу; г) суму многочленів. 26) Нехай маємо деякий многочлен а) б) значення многочлена 27) Нехай є довільний многочлен а) б) значення многочлена 28) Чи вірно, що коли многочлени рівні між собою функціонально, то вони рівні і алгебраїчно? а) так; б) ні; в) практично завжди; г) майже ніколи. 29) Чи справедливе таке твердження: а) так; б) ні; в) залежно від початкових умов; г) не знаю. 30) Чи рівносильні алгебраїчне та функціональне тлумачення поняття кореня многочлена над довільною областю цілісності: а) так; б) ні; в) за певних умов; г) можливо. 31) У кільці а) так; б) ні; в) можливо. 32) Вкажіть, які з властивостей подільності многочленів над полем а) б) в) г) 33) Чи вірно записана властивість подільності многочленів над а) так; б) ні; в) можливо; г) при певному 34) Довільний многочлен а) б) в) г) 35) Яке з тверджень неправильне: а) будь-які многочлени б) будь-які многочлени в) будь-які многочлени 36) Чи вірно: якщо а) так; б) ні; в) при певному г) при певному 37) Допишіть властивість взаємно простих многочленів а) б) в) г) 38) Якщо многочлен а) б) в) г) 39) Якщо многочлен а) звідним; б) взаємно простим; в) асоційованим; г) незвідним. 40) Допишіть властивість: ( а) б) в) г) 41) Задача 1: остачі від ділення многочлена а) б) в) 42) Задача 2: відокремити кратні множники многочлена а) б) в) 43) Задача 3: дослідити на звідність многочлен а) звідний; б) незвідний; в) не можливо визначити. 44) Задача 4: розкласти дріб а) б) в)
ТЕСТ 2
Симетричні многочлени
1) Два члени многочлена, що відрізняються лише коефіцієнтами називаються: а) взаємно простими; б) асоційованими; в) подібними; г) незвідними. 2) Степенем члена а) добуток б) різниця в) сума г) добуток 3) Який степінь многочлена а) 3; б) 4; в) 5; г) 6. 4) Який „вищий” член многочлена а) б) в) г) 5) Який старший член многочлена а) б) в) г) 6) Якщо всі члени многочлена мають однаковий степінь, то многочлен називається: а) примітивним; б) подібним; в) однорідним; г) зведеним. 7) Який з многочленів записаний лексикографічно: а) б) в) г) 8) Якщо многочлени а) примітивні; б) звідні; в) асоційовані; г) прості. 9) Многочлен а) асоційованим; б) звідним; в) симетричним; г) примітивним. 10) Який з цих многочленів симетричний: а) б) в) г) 11) Як виражається через елементарні симетричні многочлени сума а) б) в) г) 12) Нехай а) б) в) г) 13) Яке з тверджень вірне: а) б) в) г) 14) Для того, щоб многочлени а) б) в) г) 15) Дискримінант многочлена це вираз виду: а) б) в) г) 16) Для того, щоб многочлен а) б) в) г) 17) Скільки членів може мати канонічна форма однорідного многочлена другого степеня від двох змінних: а) 1; б) 2; в) 3; г) від 1 до 3. 18) Скільки членів може мати канонічна форма однорідного многочлена третього степеня від трьох змінних: а) 3; б) від 1 до 9; в) від 1 до 10; г) від 1 до 6. 19) Серед наступних одночленів вказати ті, які не можуть бути вищим членом многочлена: а) б) в) г) 20) Многочлен а) зведеним відносно змінних б) симетричним відносно змінних в) звідним відносно змінних г) однорідним відносно змінних 21) Якщо а) б) в) г) 22) Що утворює множина всіх симетричних многочленів від а) кільце з 1; б) поле з 1; в) групу з 1; г) область цілісності з 1. 23) Як позначається такий елементарний симетричний многочлен а) б) в) г) 24) Чи вірно, що а) так; б) ні; в) якщо дописати г) якщо із запису вилучити 25) Чи можна всякий симетричний многочлен від а) так; б) ні; в) залежить від вибору г) залежить від початкового многочлена. 26) Задача 1: знайти всі дійсні розв’язки системи рівнянь а) б) в) 27) Задача 2: обчислити при яких раціональних значеннях а) якщо б) якщо в) якщо 28) Задача 3: знайти цілі значення а) б) в)
ТЕСТ 3
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 600; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.20.30 (0.012 с.) |

 , де
, де 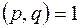 , може бути коренем рівняння з цілими коефіцієнтами?
, може бути коренем рівняння з цілими коефіцієнтами?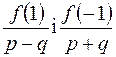 є цілими, то
є цілими, то  з цілими коефіцієнтами у полі раціональних чисел.
з цілими коефіцієнтами у полі раціональних чисел.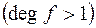 має хоч один раціональний корінь
має хоч один раціональний корінь 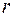 , то …
, то …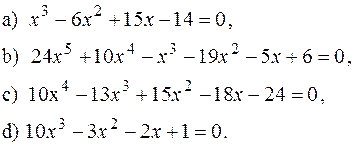



 :
: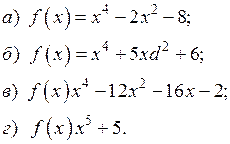

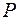 ?
? відносно поля
відносно поля 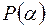 , утворене з поля
, утворене з поля  -го степеня
-го степеня 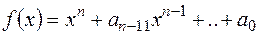 ?
?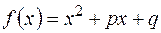 і
і 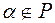 ?
? поля
поля 
 і
і  алгебраїчні. Знайти степінь числа
алгебраїчні. Знайти степінь числа  .
.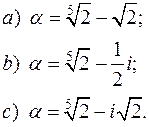

 число
число  ? В полі
? В полі 
 ?
?
 де
де 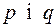 - прості числа,
- прості числа, ,
, .
. і
і  - натуральні числа, причому
- натуральні числа, причому  і
і  - не цілі. Довести, що
- не цілі. Довести, що 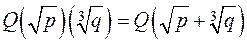 .
.
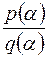 ?
? де
де  ,
, де
де 



 , де
, де  , знайти представлення для числа
, знайти представлення для числа  у вигляді
у вигляді  .
. , якщо
, якщо 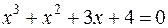 .
.
 чи
чи  вираз:
вираз: ;
; ;
; ;
; .
. :
: називається такий запис:
називається такий запис: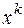 ;
; над полем
над полем  ;
; над полем
над полем  ;
; над кільцем
над кільцем  ;
; над полем
над полем  .
. …
… ;
;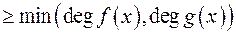 ;
; ;
; .
. та
та  многочлен з кільця
многочлен з кільця  та
та 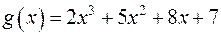
 ;
; ;
; ;
; .
. многочлени
многочлени  …, якщо вони відрізняються лише множником, який є відмінною від нуля константою.
…, якщо вони відрізняються лише множником, який є відмінною від нуля константою. з кільця
з кільця  :
: у виразі
у виразі  :
: :
: такий, що
такий, що :
: , то
, то  називається …
називається … називається … у полі
називається … у полі  і в кільці
і в кільці 
 ,
,  і
і  .
. , де многочлен
, де многочлен  , то многочлени
, то многочлени  :
: називається неправильним, якщо …
називається неправильним, якщо …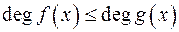 ;
;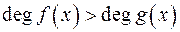 ;
;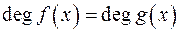 ;
;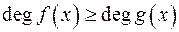 .
.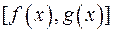 – це …
– це …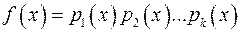 :
: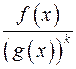 , де
, де 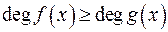 ,
, 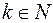 ;
;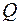 :
: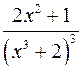 ;
;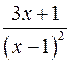 ;
;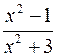 ;
;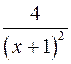 .
. означає:
означає: - корінь многочлена
- корінь многочлена 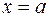 .
.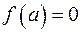 :
: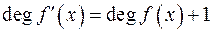 ?
?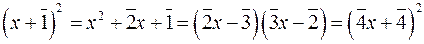 . Чи не суперечать вони теоремі про єдиність розкладу многочлена на незвідні множники у кільці
. Чи не суперечать вони теоремі про єдиність розкладу многочлена на незвідні множники у кільці 

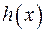 ;
;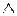
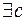
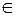 P [x]
P [x] 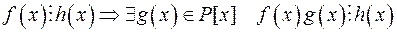 :
: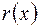 належать Р[x] і визначаються однозначно, тобто
належать Р[x] і визначаються однозначно, тобто 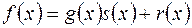 , причому …
, причому …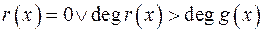 ;
;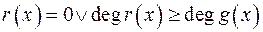 ;
;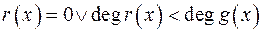 ;
;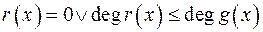 .
.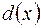 – НСД многочленів
– НСД многочленів  0
0  – НСК многочленів
– НСК многочленів 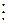

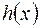
 …
…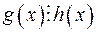 ;
;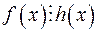 ;
;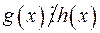 .
.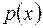 є незвідним над полем
є незвідним над полем  , то для будь-якого многочлена
, то для будь-якого многочлена 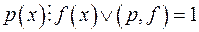 ;
;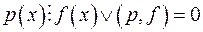 ;
;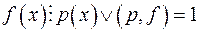 ;
;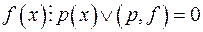 .
.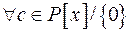 многочлен
многочлен 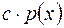 є …
є …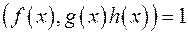 ;
;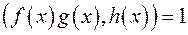 ;
;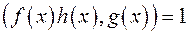 ;
;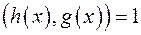 .
.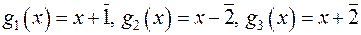 відповідно дорівнюють
відповідно дорівнюють 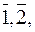 та
та 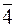 . Знайти остачу від ділення цього многочлена на
. Знайти остачу від ділення цього многочлена на  :
: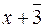 ;
;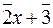 ;
;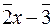 ;
; :
: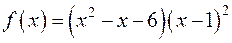 ;
;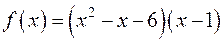 ;
;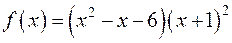 .
.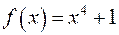 в
в  :
: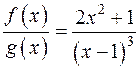 на елементарні дроби над полем
на елементарні дроби над полем  :
: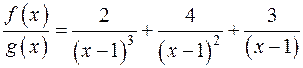 ;
;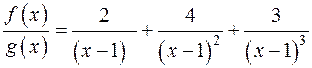 ;
;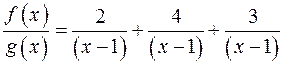 .
.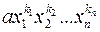 називається:
називається: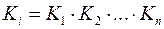 ;
;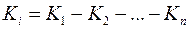 ;
;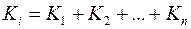 ;
;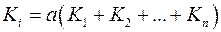 .
.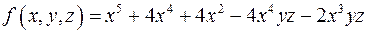 :
: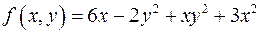 :
: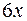 ;
;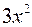 ;
;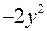 ;
;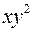 .
.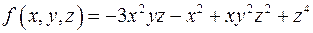 ;
;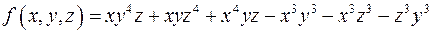 ;
;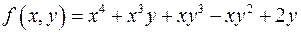 ;
;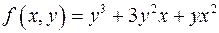 .
.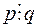 , то вони:
, то вони: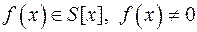 називається …, якщо НСД його коефіцієнтів рівний 1.
називається …, якщо НСД його коефіцієнтів рівний 1.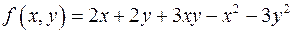 ;
;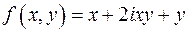 ;
;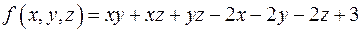 ;
;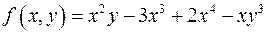 .
.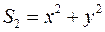 :
: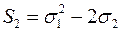 ;
;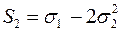 ;
;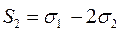 ;
;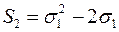 .
. і
і 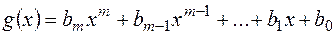 , де
, де 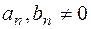 і
і 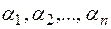 - корені
- корені 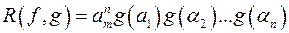 ;
;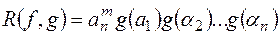 ;
;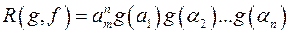 ;
;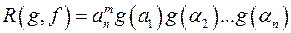 .
.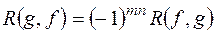 ;
;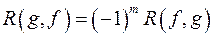 ;
;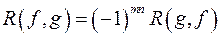 ;
;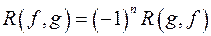 .
.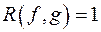 ;
;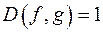 ;
;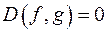 ;
; .
.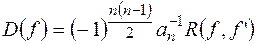 ;
;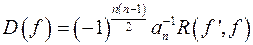 ;
;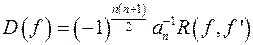 ;
;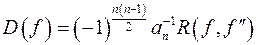 .
.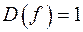 ;
;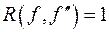 ;
; ;
;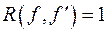 .
.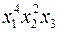 ;
;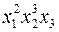 ;
;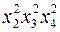 ;
;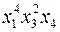 .
.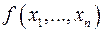 називається …, якщо внаслідок довільної перестановки змінних
називається …, якщо внаслідок довільної перестановки змінних 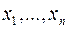 утворюється многочлен, рівний даному:
утворюється многочлен, рівний даному: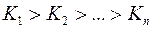 ;
;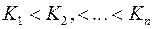 ;
;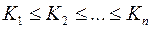 ;
;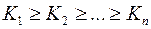 .
.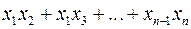 :
: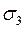 ;
;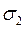 ;
;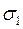 ;
;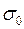 .
.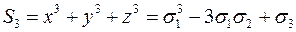 :
: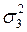 ;
;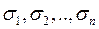 :
: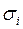 ;
;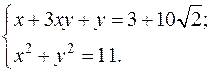
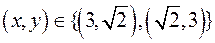 ;
;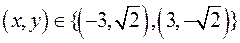 ;
;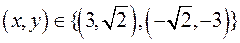 .
. мають спільний корінь многочлени
мають спільний корінь многочлени 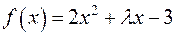 і
і 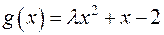 :
: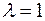 , то
, то 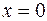 ;
;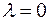 , то
, то 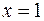 .
.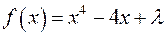 :
: ;
;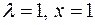 ;
;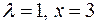 .
.


