
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Произведение двух многочленов с целыми коэффициентами.Содержание книги
Поиск на нашем сайте
Произведение двух многочленов с целыми коэффициентами.
Определение: многочлен f(x) с целыми коэффициентами называется примитивным, если НОД всех его коэффициентов равен 1.
Лемма 3. Произведение двух примитивных многочленов также является примитивным многочленом.
Лемма 4: если многочлен
до-во: т.к. f(x) – приводим, то его можно представить в виде Пусть до-но.
Алгебраическая замкнутость поля.
Определение: поле Р называется алгебраически замкнутым, если всякий многочлен из кольца
Определение: поле Р называется алгебраически замкнутым, если всякий многочлен из
Покажем, что определения эквивалентны. Пусть поле Р алгебраически замкнуто по первому определению:
Поле Р алгебраически замкнуто по первому определению.
Основная теорема алгебры.
Определение: функция Функция f(x) называется непрерывной, если она непрерывна в каждой точке области определения.
Лемма 1:всякий многочлен Лемма 2: модуль многочлена
Следствие: если последовательность комплексных чисел Следствие: если последовательность комплексных чисел Лемма 3 (Доломбера): пусть Лемма 4 (о возрастании модуля многочлена): пусть Теорема (основная теорема алгебры): всякий многочлен до-во: Обозначим через M множество всех значений модуля многочлена f (x). Пусть множество М всех значений модуля многочлена
Если l ≠ 0, то по лемме 3 существует такое комплексное число c, что Это противоречит тому, что l – точная нижняя грань множества M ⇨ l= 0 и до-но. Лемма о высшем члене многочлена. Лемма 2.1. (о высшем члене многочлена). Высший член произведения двух многочленов Доказательство. Расположим члены в многочленах
Найдём произведение Далее умножим все члены многочлена Получим группу членов, высшим из которых будет:
Наконец, все члены многочлена
Очевидно, что высший член произведения Произведение двух многочленов с целыми коэффициентами.
Определение: многочлен f(x) с целыми коэффициентами называется примитивным, если НОД всех его коэффициентов равен 1.
Лемма 3. Произведение двух примитивных многочленов также является примитивным многочленом.
Лемма 4: если многочлен
до-во: т.к. f(x) – приводим, то его можно представить в виде Пусть до-но.
|
||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 722; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.221.113 (0.01 с.) |

 с целыми коэффициентами приводим над полем Q, то его можно представить в виде произведения двух многочленов с целыми коэффициентами, степень каждого из которых меньше степени многочлена
с целыми коэффициентами приводим над полем Q, то его можно представить в виде произведения двух многочленов с целыми коэффициентами, степень каждого из которых меньше степени многочлена  .
.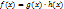 ,
,  ,
,  ,
,  и
и  - многочлены с рациональными коэффициентами.
- многочлены с рациональными коэффициентами. – НОК всех знаменателей коэффициентов многочленов
– НОК всех знаменателей коэффициентов многочленов 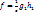 , где
, где 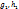 – многочлены с целыми коэффициентами. Если
– многочлены с целыми коэффициентами. Если 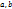 – НОД коэффициентов многочленов
– НОД коэффициентов многочленов  , где
, где  , где
, где  , таким образом из
, таким образом из 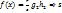 делит все коэффициенты многочлена
делит все коэффициенты многочлена  . По лемме 3 этот многочлен является примитивным ⇨
. По лемме 3 этот многочлен является примитивным ⇨  .
. степени
степени 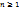 разлагается над полем Р в произведение линейных множителей.
разлагается над полем Р в произведение линейных множителей. , где
, где  - элементы поля Р ⇨
- элементы поля Р ⇨ 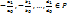 - это корни ⇨ Р алгебраически замкнуто по второму определению.
- это корни ⇨ Р алгебраически замкнуто по второму определению. Пусть поле Р алгебраически замкнуто по второму определению, т.е. всякий многочлен
Пусть поле Р алгебраически замкнуто по второму определению, т.е. всякий многочлен  – корень
– корень 




 называется непрерывной в точке
называется непрерывной в точке  , когда для любого сколь угодно малого действительного числа
, когда для любого сколь угодно малого действительного числа  существует
существует 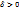 , что
, что  удовлетворяющего неравенству
удовлетворяющего неравенству  будет выполнено неравенство
будет выполнено неравенство  ,
,  - действительные
- действительные  .
. является непрерывной функцией.
является непрерывной функцией. сходится к
сходится к  , то
, то 
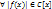 , то
, то 
 , то существует комплексное число C, что
, то существует комплексное число C, что  .
. - последовательность комплексных чисел такая что
- последовательность комплексных чисел такая что 
 степени
степени  . Так как для любого C – комплексного,
. Так как для любого C – комплексного,  – неотрицательное действительное число, то множество M ограничено снизу. Из курса математического анализа известно, что всякое множество действительных чисел, ограниченное снизу, имеет точную нижнюю грань. Обозначим через l точную нижнюю грань множества M. Тогда, в частности, для любого натурального числа k можно подобрать такое комплексное число
– неотрицательное действительное число, то множество M ограничено снизу. Из курса математического анализа известно, что всякое множество действительных чисел, ограниченное снизу, имеет точную нижнюю грань. Обозначим через l точную нижнюю грань множества M. Тогда, в частности, для любого натурального числа k можно подобрать такое комплексное число  , что
, что  . Если бы было не так, то
. Если бы было не так, то 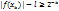 ,
,  и l не было бы нижней гранью множества M. Из (1) следует
и l не было бы нижней гранью множества M. Из (1) следует 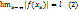 . Если построенная последовательность
. Если построенная последовательность 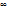 .
.  . По лемме 4
. По лемме 4  что противоречит (2). ⇨ что последовательность
что противоречит (2). ⇨ что последовательность 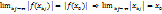
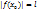
 .
.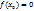 и ⇨
и ⇨  – комплексный корень.
– комплексный корень. и
и  и
и  ;
;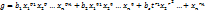 ;
; следующим образом: вначале умножим последовательно все члены многочлена,
следующим образом: вначале умножим последовательно все члены многочлена,  начиная с первого на первый член многочлена
начиная с первого на первый член многочлена  -(3)’
-(3)’ -(3) и т.д.
-(3) и т.д. Получим группу членов высшим из которых будет:
Получим группу членов высшим из которых будет:
 следует искать среди высших членов найденных групп. Но они в свою очередь составляют группу членов, полученных последовательным умножением многочлена
следует искать среди высших членов найденных групп. Но они в свою очередь составляют группу членов, полученных последовательным умножением многочлена  . Следовательно, высший член произведения
. Следовательно, высший член произведения 


