
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основная теорема о симметрических многочленах.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Теорема (основная теорема о симметрических многочленах): всякий симметрический многочлен
До-во: расположим члены многочлена
Рассмотрим выражение Подберём показатели Высшими членами многочленов Тогда по лемме о высшем члене многочлена высшим членом многочлена (9) будет являться выражение:
Это выражение совпадёт с (7) тогда и только тогда, когда будут выполняться равенства:
…………………….
Таким образом, высший член многочлена
совпадает с высшим членом многочлена Вычтем из многочлена Пусть Получим В результате вычитания высший член многочлена Таким образом, в конечном итоге будем иметь:
…………………………………………………….
до-но. Следствие: пусть
41. Условие при которых многочлены
Теорема: многочлены
1) 2) многочлены
3) по крайней мере, один из многочленов
до-во: Необходимость. Пусть многочлены f (x) и g (x) имеют общий корень α. Тогда они представимы в виде
Многочлены f (x) и g (x) в равенствах (1) удовлетворяют условиям 1-3теоремы. Действительно, умножив обе части первого равенства на h (x) получим:
Таким образом, выполняется условие 2. Наконец, хотя бы один из многочленов q (x) и h (x) отличен от нуля, в противном случае оба многочлена f (x) и g (x) были бы равны нулю, что противоречит условию. до-но.
42. Результант многочленов
Определение: результантом многочленов
Теорема: многочлены Следствие: если результант f и g равен нулю, то либо эти многочлены имеют общий корень, либо оба коэффициента
Результант многочленов находит практическое применение при решении системы двух уравнений с двумя переменными, из которых хотя быодно нелинейное, т.е. системы вида:
где Расположим члены в многочленах
Где Пусть Таким образом, систему (4) можно решать в следующем порядке: 1. Строится результант 2. Находятся корни результанта 3. Найденные корни результанта
4. Составляются всевозможные пары чисел Эти пары и составляют множество решений системы (4).
43. Необходимое и достаточное условие существования общего корня у многочленов Теорема: многочлены Следствие: если результант многочленов
|
||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 1351; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.141.142 (0.011 с.) |

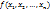 из кольца
из кольца  можно представить в виде многочлена от элементарных симметрических многочленов
можно представить в виде многочлена от элементарных симметрических многочленов 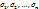 над полем
над полем  , то есть
, то есть  , где
, где  многочлен из кольца
многочлен из кольца  в словарном порядке. Пусть при этом
в словарном порядке. Пусть при этом 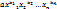 - (7) – высший член многочлена
- (7) – высший член многочлена 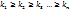 - (8)
- (8) - (9).
- (9). так, чтобы высший член многочлена (9) совпал с высшим членом многочлена
так, чтобы высший член многочлена (9) совпал с высшим членом многочлена  ,
, 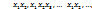
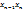 .
. –(10);
–(10);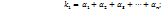



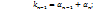

 Из этой системы находим:
Из этой системы находим: ;
;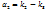 ;
;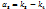 ;
;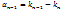 ;
; ;
;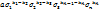 - (11)
- (11)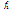 , то есть
, то есть  В результате вычитания высший член многочлена
В результате вычитания высший член многочлена  уничтожится и все члены многочлена
уничтожится и все члены многочлена 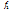 будут ниже (7).
будут ниже (7). и
и  – (12) высший член многочлена
– (12) высший член многочлена  .
.
 уничтожится и все члены многочлена
уничтожится и все члены многочлена  будут ниже и т.д. Этот процесс понижения членов многочленов не может продолжаться бесконечно. Действительно, пусть на каком-то
будут ниже и т.д. Этот процесс понижения членов многочленов не может продолжаться бесконечно. Действительно, пусть на каком-то  -ом шаге в результате вычитания мы получим многочлен
-ом шаге в результате вычитания мы получим многочлен  , высшим членом которого будет выражение
, высшим членом которого будет выражение 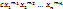 (13). По свойству 3 справедливы неравенства
(13). По свойству 3 справедливы неравенства 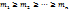 . При этом
. При этом 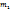 ≤
≤  , так как член (13) ниже члена (7). Этим условиям может удовлетворять лишь конечное множество упорядоченных систем целых неотрицательных чисел
, так как член (13) ниже члена (7). Этим условиям может удовлетворять лишь конечное множество упорядоченных систем целых неотрицательных чисел 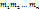 .
.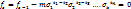 ;
;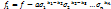 ;
; ;
;

 +…+
+…+ 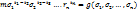 .
.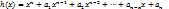 – многочлен из кольца
– многочлен из кольца 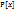 и пусть
и пусть  ,
,  ,
,  принимает значение принадлежащее полю
принимает значение принадлежащее полю 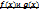 имеют общий корень
имеют общий корень у которых, по крайней мере, один из коэффициентов
у которых, по крайней мере, один из коэффициентов  и
и  отличен от нуля, т. и т.т. имеют общий корень, когда существуют многочлены
отличен от нуля, т. и т.т. имеют общий корень, когда существуют многочлены 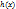 и
и 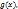 удовлетворяющие следующим условиям:
удовлетворяющие следующим условиям:
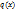 представимы в виде
представимы в виде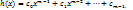 ;
;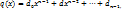

 (1)
(1)
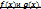 Решение системы двух уравнений с двумя переменными с помощью результанта.
Решение системы двух уравнений с двумя переменными с помощью результанта. называется определитель
называется определитель  определяемый равенством:
определяемый равенством: =
= 
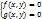 -(4)
-(4)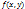 и
и 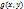 многочлены из кольца
многочлены из кольца 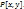
 по убыванию степеней одной изпеременных, например
по убыванию степеней одной изпеременных, например  .
. ;
; ;
;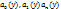 ,
, 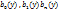 – многочлены от одной переменной
– многочлены от одной переменной  . Рассматривая многочлены
. Рассматривая многочлены  как многочлены от одной переменной
как многочлены от одной переменной 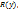 который очевидно является многочленом от одной переменной
который очевидно является многочленом от одной переменной  .
.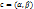 – решение системы (4). Тогда многочлены
– решение системы (4). Тогда многочлены  и
и 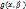 имеют общий корень
имеют общий корень  . По теореме 4.2 в таком случае
. По теореме 4.2 в таком случае  С другой стороны, если
С другой стороны, если 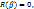 то либо оба коэффициента
то либо оба коэффициента 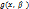 имеют общий корень α. Во втором случае вектор
имеют общий корень α. Во втором случае вектор  является решением системы (4).
является решением системы (4).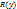 многочленов
многочленов 
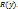
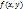 и
и  Пусть, например,
Пусть, например,  – корень результанта
– корень результанта 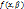 и
и 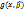 от одной переменной
от одной переменной 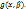
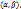 где
где  – корень многочлена
– корень многочлена 


