Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Многочлени над різними полямиСодержание книги
Поиск на нашем сайте
1) Коженмногочлен, степінь якого більша за 1 є … у полі а) незвідним; б) звідним; в) зведеним; г) примітивним. 2) Скільки коренів має многочлен а) рівно б) рівно в) рівно г) не менше 3) Який вигляд має дискримінант кубічного рівняння а) б) в) г) 4) При якій умові кубічне рівняння має один дійсний корінь і два комплексних спряжених кореня: а) б) в) г) 5) При якій умові кубічне рівняння має три дійсних корені (два з яких рівні): а) б) в) г) 6) При якій умові кубічне рівняння має три різних дійсних кореня: а) б) в) г) 7) Довільний многочлен ненульового степеня з комплексними коефіцієнтами має хоча б один … корінь (основна теорема теорії многочленів): а) цілий; б) раціональний; в) дійсний; г) комплексний. 8) Якщо комплексне число а) не є коренем цього многочлена; б) є коренем цього ж многочлена; в) є коренем многочлена з протилежними знаками; г) є коренем многочлена з коефіцієнтами, оберненими до 9) Якщо комплексне число а) б) в) г) нульової кратності. 10) Всі дійсні корені рівняння а) б) в) г) 11) Щоб відокремити дійсні корені многочлена а) не лежить жодного кореня; б) лежить один корінь; в) лежать два кореня; г) лежать всі корені. 12) Якщо а) не зміниться; б) зросте на 1; в) зменшиться на 1. 13) Якщо а) б) в) г) 14) Яким є поле розкладу многочлена а) Z; б) Q; в) R; г) C. 15) Яким є поле розкладу многочлена а) Z; б) Q; в) R; г) C. 16) Яким є поле розкладу многочлена а) Z; б) Q; в) R; г) C. 17) Коренем многочлена а) б) 3; в) г) 18) Чи є звідним над полем С многочлен а) так; б) ні; в) при певному г) можливо. 19) Яке максимальне число змін знаків може мати многочлен а) б) в) г) 20) Щоб дріб а) б) в) г) 21) Щоб дріб а) б) в) г) 22) Якщо в многочлені з цілими коефіцієнтами а) б) в) г) 23) Многочлени а) так; б) ні; в) при певному г) при певному 24) Чи може незвідний у кільці а) так; б) ні; в) при певному г) при певному 25) Нехай є многочлен а) б) в) г) 26) Якщо а) не зміниться; б) зменшиться на 1; в) збільшиться на 1. 27) Задача 1: знайти многочлен найменшого степеня, в якого число а) б) в) г) 28) Задача 2: знайти суму квадратів коренів многочлена а) б) в) 29) Задача 3: розв’язати рівняння а) б) в) 30) Задача 4: відокремити дійсні корені многочлена а) один комплексний корінь в інтервалі б) два дійсних кореня в інтервалі в) один дійсний корінь в інтервалі 31) Задача 5: знайти всі раціональні корені многочлена а) б) в) раціональних коренів немає.
ТЕСТ 4
Алгебраїчні розширення 1) Розширення а) нескінченим; б) алгебраїчним; в) скінченим; г) трансцендентним. 2) Розширення а) б) в) г) 3) Які з чисел є алгебраїчними: а) б) в) г) 4) Говорять, що множина а) так; б) ні; в) за певних умов. 5) Нехай а) б) в) г) 6) Яким числом є сума довільного раціонального і трансцендентного чисел: а) раціональним; б) алгебраїчним; в) дійсним; г) трансцендентним. 7) Яку алгебраїчну структуру відносно операції додавання і множення утворюють алгебраїчні числа: а) групу; б) кільце; в) поле; г) тіло. 8) Нехай поле а) 1; б) 2; в) 5; г) 10; д) всі перераховані. 9) Нехай поле а) так; б) ні; в) лише одне. 10) Якщо число а) звідний; б) мінімальний; в) симетричний; г) асоційований. 11) Мінімальне розширення поля а) складним розширенням поля б) максимальним розширенням поля в) простим розширенням поля г) алгебраїчним розширенням поля 12) Якщо а) простим алгебраїчним розширенням поля б) складним алгебраїчним розширенням поля в) простим трансцендентним розширенням поля г) складним трансцендентним розширенням поля 13) Чи вірно, що кожне складне алгебраїчне розширення поля а) так; б) ні; в) за певних умов. 14) Нехай а) дійсне; б) алгебраїчне; в) трансцендентне; г) комплексне. 15) Задача 1: довести, що число а) б) в) г) 16) Задача 1: позбавитись віз ірраціональності в знаменнику дробу а) б) в) г)
ПІДСУМКОВИЙ ТЕСТ
Теорія многочленів 1)Вираз виду:
називається ____________________ над ______________. 2) Степінь многочлена позначається ________ і канонічна форма многочлена це _________________________________________ 3) Алгебраїчна рівність многочленів ________________________ _____________________________________________________, а функціональна - ______________________________________ _____________________________________________________. 4) Якщо многочлени рівні алгебраїчно, то вони рівні і _________. Чи справедливе обернене твердження: ___________________. 5) Властивості подільності многочленів:_____________________ ______________________________________________________ ______________________________________________________ 6) Сформулювати теорему 7) Якщо б) 8) 9) 10) Якщо 11) Заповнити пусті місця: де ___________________________________________________. 12) Многочлен 13) Властивості незвідних многочленів: __________________ 14) Якщо 15) Теорема Кронекера: _______________________________ 16) Поле розкладу многочлена - це ______________________ 17) Для того, щоб 18) Нехай
Що можна сказати про число 19) Раціональний дріб Навести приклади правильного дробу: ____________________. 20) Елементарний дріб – це ____________________________ 21) Якщо 22) Кожен правильний дріб виду 23) Многочлен 24) Многочлен називається однорідним, якщо _____________ Приклад:_____________________________________________. 25) Многочлен Приклади несиметричних многочленів: ___________________ 26) Властивості симетричних многочленів:__________________________________________ 27) Елементарні симетричні многочлени – це 28) Основна теорема симетричних многочленів:___________ 29) Степеневу суму третього порядку від двох змінних представити через основні симетричні многочлени: _________ 30) Теорема Вієта:_____________________________________ 31) 32) Якщо 33) 34) Якщо 35) Многочлен третього степеня над полем а) принаймні один дійсний корінь; б) два дійсних і один комплексний корені. Підкреслити правильну відповідь. Чи існують інші варіанти? Якщо так, то вказати їх: _________________________________ 36) Будь-який многочлен ненульового степеня з комплексними коефіцієнтами має_________________________ 37) Многочлен 38) Якщо 39) Що можна сказати про звідність довільного многочлена над 40) Всі дійсні корені многочлена 41) Правило Декарта: _________________________________ 42) Що означає відокремити дійсні корені многочлена: _____ 43) Як утворюється ряд Штурма: _______________________ 44) Властивості ряду Штурма: _________________________ 45) Теорема Штурма: __________________________________ 46) Щоб число 47) Для того, щоб 48) Критерій Ейзенштейна: ____________________________ 49) Число 50) Мінімальний многочлен – це многочлен, що задовольняє умови:___________________________________________________________________________________________________________________________________________________________.
ВІДПОВІДІ Розділ I § 1 1.
2.
3.
4. 5. 7. 8. - 1. 9. 10. 11. 12. 13. § 2 1. 2. 3. 4. 5. 6. 7.
9. 10.
11.
§ 3 1.
2.
3.
4. 5.
6. 7. 8. 9. 10. 11. § 4 2.
3. 4.
5. 6. 7.
8. 9. 10. Розділ II § 5 1.
2.
3.
4.
5. 6. 8. § 6 1.
2. 3.
4. 5. 6. 7. 8. 9. 12.
§ 7 1. -7. 2. 3. 5. 6. Розділ III § 8 1.
2. 3. 23. 4. 5.
6. 7. 8. Так. 9. § 9 1.
2.
3.
4.
5.
§ 10 1.
2.
| ||||||||||||||||||||
|
| Поделиться: |

 :
: -го степеня над полем
-го степеня над полем  ;
; ;
; :
: ;
; ;
; ;
; .
. ;
; ;
; ;
; .
. - є коренем многочлена
- є коренем многочлена  з дійсними коефіцієнтами, то спряжене комплексне
з дійсними коефіцієнтами, то спряжене комплексне  …
… -ї кратності многочлена
-ї кратності многочлена  -ї кратності;
-ї кратності; -ї кратності;
-ї кратності; містяться в інтервалі
містяться в інтервалі  , де
, де  і ...
і ... ;
; ;
; ;
; .
. необхідно знайти інтервали, у яких …
необхідно знайти інтервали, у яких … , зростаючи, проходить через корінь якої-небудь проміжної функції ряду, але не проходить через корінь
, зростаючи, проходить через корінь якої-небудь проміжної функції ряду, але не проходить через корінь  , то число змін знаків у ряді Штурма при цьому …
, то число змін знаків у ряді Штурма при цьому … і
і  (
( ) – довільні дійсні числа, які не є коренями
) – довільні дійсні числа, які не є коренями  дійсних коренів многочлена
дійсних коренів многочлена  ) дорівнює
) дорівнює  …, де
…, де  і
і  є число змін знаків у ряді Штурма відповідно у точках
є число змін знаків у ряді Штурма відповідно у точках  ;
; ;
; ;
; .
. :
: :
: :
:
 ;
; ;
; .
. :
: .
. , де (
, де ( ) = 1 було коренем рівняння з цілими коефіцієнтами необхідно, щоб
) = 1 було коренем рівняння з цілими коефіцієнтами необхідно, щоб  , а
, а  - …
- … , необхідно, щоб при довільному цілому
, необхідно, щоб при довільному цілому 
 , де
, де  0;
0; , де
, де  0;
0; коефіцієнти
коефіцієнти  діляться на деяке просте число
діляться на деяке просте число 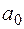 …, а старший коефіцієнт
…, а старший коефіцієнт  …, то многочлен
…, то многочлен  , і
, і  ;
; з кільця
з кільця  є взаємно простими. Чи можуть вони мати спільний комплексний корінь
є взаємно простими. Чи можуть вони мати спільний комплексний корінь  :
: . Яка заміна приводить до многочлена виду
. Яка заміна приводить до многочлена виду  ;
; ;
; ;
; .
. ;
; ;
; ;
;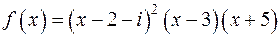 .
. :
: ;
; ;
; .
. :
: ;
; ;
; .
. :
: ;
; :
: ;
; ;
; поля
поля 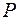 називається ..., якщо в полі
називається ..., якщо в полі  , що будь-який елемент
, що будь-який елемент  є лінійною комбінацією цих елементів з коефіцієнтами з поля
є лінійною комбінацією цих елементів з коефіцієнтами з поля  , якщо існує такий ланцюжок розширень ..., що
, якщо існує такий ланцюжок розширень ..., що  :
: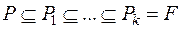 ;
; ;
; ;
; .
. ;
; ;
; ;
; .
. є зчисленою, якщо існує взаємно однозначне відображення множини
є зчисленою, якщо існує взаємно однозначне відображення множини  . Чи є множина всіх алгебраїчних чисел зчисленою?
. Чи є множина всіх алгебраїчних чисел зчисленою? - алгебраїчне,
- алгебраїчне,  - трансцендентне і
- трансцендентне і  ;
; ;
; ;
; .
.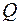 степеня 10. Якого степеня алгебраїчні числа містяться в полі
степеня 10. Якого степеня алгебраїчні числа містяться в полі  існує єдиний зведений многочлен
існує єдиний зведений многочлен  і степінь
і степінь  , називається …, утвореним приєднанням числа
, називається …, утвореним приєднанням числа  називається …
називається …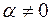 - алгебраїчне число. Яким буде число
- алгебраїчне число. Яким буде число  , обернене до
, обернене до  - алгебраїчне і знайти його мінімальний многочлен:
- алгебраїчне і знайти його мінімальний многочлен: ;
; ;
; ;
; .
. , де
, де  - корінь рівняння
- корінь рівняння  :
: ;
; ;
; ;
; .
. ,
,  – _____________________________________,
– _____________________________________, - ___________________________________________,
- ___________________________________________, :_____________
:_____________ , то а)
, то а)  - ____________________________.
- ____________________________.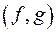 - _______________________________________________.
- _______________________________________________. _______________________________________________.
_______________________________________________. , то _________________________________.
, то _________________________________. ______+
______+  _____,
_____, і
і  , то _______________
, то _______________ ? Чому рівна остача від ділення многочлена
? Чому рівна остача від ділення многочлена  на
на  _______________________________________________.
_______________________________________________. називається правильним, якщо
називається правильним, якщо  , то
, то  ______________,
______________, , де
, де  є многочленом від __________змінних. Його вищий член __________, степінь ___________, лексикографічний запис ___
є многочленом від __________змінних. Його вищий член __________, степінь ___________, лексикографічний запис ___ є симетричним, якщо __________
є симетричним, якщо __________ , де
, де  - ______
- ______ , то ________________________________
, то ________________________________ . Заповнити пропущені місця.
. Заповнити пропущені місця. , то _________________________________
, то _________________________________ має:
має: є коренем
є коренем 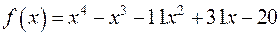 , то і
, то і  _____________________.Сформулювати теорему на основі якої було зроблено висновок_____________________________
_____________________.Сформулювати теорему на основі якої було зроблено висновок_____________________________ містяться в інтервалі: ______ ________, де __________________________________________.
містяться в інтервалі: ______ ________, де __________________________________________. , де
, де 


 .
. ;
; .
.






 .
.



 .
.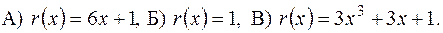














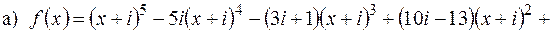











 ;
;


 ;
;



























 .
.



















 .
.