Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Застосування симетричних многочленів до розв’язування деяких задач з елементарної алгебриСодержание книги
Поиск на нашем сайте
Задачі 1) У множині дійсних чисел розв’язати системи: 2) Розв’язати систему ірраціональних рівнянь: 3) Розв’язати системи рівнянь, звівши їх за допомогою допоміжних змінних до симетричних многочленів: 4) Розв’язати такі рівняння: 5) Скоротити дріб 6) Скласти квадратне рівняння, коренями якого є куби коренів рівняння 7) Скласти квадратне рівняння, коренями якого є 8) Знайти многочлен третього степеня, коренями якого є: 9) Знайти многочлен четвертого степеня, коренями якого є: 10) Довести такі тотожності: 11) Довести, що коли 12) Розкласти на незвідні над полем R множники симетричний однорідний многочлен
Дискримінант та результант двох многочленів, їх властивості і застосування до розв'язування задач Питання для самоконтролю:
1) Що називається результантом? 2) Назвіть властивості результанту. 3) Щоб многочлени 4) Як записується результант у формі Сільвестра? 5) Якщо 6) Дискримінант двох многочленів - це … 7) Умова існування кратного кореня. 8) Який алгоритм виключення невідомих з системи рівнянь: Задачі
1) Обчислити результант многочленів: 2) При якому значенні
3) Обчислити дискримінант многочленів: 4) Довести, що дискримінант многочлена 5) При якому значенні 6) Розв’язати системи рівнянь:
Розділ III.Многочлени над полем комплексних чисел і над полем дійсних чисел
Многочлени над полем комплексних чисел. Алгебраїчна замкненість поля комплексних чисел Питання для самоконтролю: 1) Яке поле 2) Скільки дійсних і комплексних коренів має многочлен з дійсними коефіцієнтами? 3) Сформулюйте основну теорему теорії многочленів. 4) Які многочлени називаються звідними у полі комплексних чисел? 5) Необхідна і достатня умова незвідності многочлена у 6) Скільки коренів має многочлен
Задачі
1) Знайти многочлен найменшого степеня, в якого: 2) Знайти многочлен найменшого степеня з дійсними коефіцієнтами, якщо 3) Знайти суму квадратів коренів многочлена 5) Сума двох коренів рівняння 6) Використовуючи формули Вієта, побудувати многочлен за його коренями:
7) Знайти зведений многочлен, в якого корені задовольняють умову: 8) Корені многочлена 9) Чи утворюють корені рівняння 10) Визначте
Многочлени над полем дійсних чисел Питання для самоконтролю: 1) Що можна сказати про спряжене комплексне число 2) Який многочлен є звідним у полі дійсних чисел? 3) Як можна многочлен розкласти над полем дійсних чисел на незвідні множники? Задачі
1) Розв’язати рівняння:
2) Знайти нормований многочлен найменшого степеня з дійсними коефіцієнтами, що має: а) простий корінь b) простий корінь с) трикратний корінь 3) Знаючи, що число
4) Розкласти многочлен
5) Яким умовам повинні задовольняти дійсні коефіцієнти многочлена:
Рівняння третього степеня Питання для самоконтролю: 1) Яке рівняння називається рівнянням третього степеня? 2) Рівняння 3) Як називається вираз 4) Як знайти корені рівняння 5) Коли рівняння 6) Якщо 7) Рівняння 8) U1 i V1 – це … 9) З якої умови знаходиться числа U1 i V1?
Задачі
1) Звести кубічне рівняння до виду, у якому відсутній доданок з невідомим у другому степені:
2) Розв’язати рівняння:
3) При яких дійсних значеннях 4) Які корені залежно від значення числа 5) Розв’язати рівняння 6) Розв’язати рівняння 7) Розв’язати кубічне рівняння
§ 11. Відокремлення дійсних коренів многочленів.
Питання для самоконтролю: 1) Як розташовані комплексні корені з дійсними коефіцієнтами відносно дійсної осі? 2) Де розміщені всі дійсні корені рівняння 3) Число М є верхньою межею додатних коренів многочлена 4) Кількість змін знаків деякої впорядкованої послідовності дійсних чисел 5) Сформулюйте правило Декарта. 6) Яка заміна використовується для знаходження кількості від’ємних коренів многочлена 7) Щоб побудувати ряд Штурма необхідно… 8) Сформулювати теорему Штурма. 9) Чи мають дві сусідні функції ряду Штурма спільні корені? 10) Якщо 11) Якщо 12) Якщо
Задачі
1) Знайти верхню межу дійсних коренів многочлена методом Ньютона:
2) Знайти нижню межу дійсних коренів многочлена методом Ньютона:
3) Обмежити зверху і знизу дійсні корені многочленів:
4) Знайти число дійсних коренів для многочленів: 5) Відокремити дійсні корені многочленів: 6) Оцінити за правилом Декарта число додатніх і від’ємних коренів многочлена
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 810; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.33.239 (0.006 с.) |

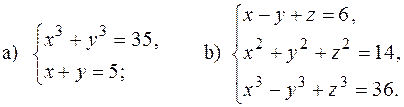





 , якщо відомо, що
, якщо відомо, що 




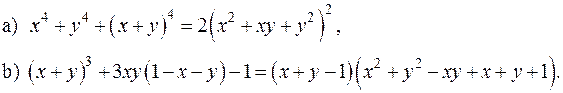
 , то
, то 

 і
і 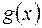 мали спільний корінь необхідною і достатньою умовою є …
мали спільний корінь необхідною і достатньою умовою є …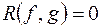 , то …
, то …

 мають спільні корені слідуючі многочлени:
мають спільні корені слідуючі многочлени:

 дорівнює дискримінанту многочлена
дорівнює дискримінанту многочлена 

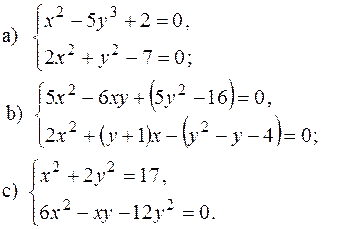
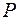 називається алгебраїчно замкненим?
називається алгебраїчно замкненим? -го степеня у полі комплексних чисел?
-го степеня у полі комплексних чисел? – прості;
– прості; – його потрійний корінь.
– його потрійний корінь.
 дорівнює 1. Визначити
дорівнює 1. Визначити 
 , а
, а  ,
,  ,
,  є коренями многочлена
є коренями многочлена  .
. .
. арифметичну прогресію?
арифметичну прогресію? так, щоб один з коренів многочлена
так, щоб один з коренів многочлена 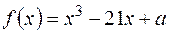 був рівний подвоєному другому кореню.
був рівний подвоєному другому кореню.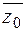 , якщо комплексне число
, якщо комплексне число  є коренем многочлена
є коренем многочлена  з дійсними коефіцієнтами?
з дійсними коефіцієнтами? , якщо
, якщо  ;
; , якщо
, якщо  ;
; , якщо
, якщо  .
.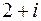 і двократний корінь 1;
і двократний корінь 1; і двократні корені
і двократні корені  та
та  ;
; є коренем многочлена
є коренем многочлена 

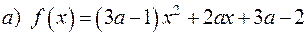 , щоб він мав два різних дійсних корені;
, щоб він мав два різних дійсних корені; , щоб він мав один дійсний корінь.
, щоб він мав один дійсний корінь. третього степеня зводиться до рівняння виду
третього степеня зводиться до рівняння виду  за допомогою …
за допомогою … ?
? , то які корені має рівняння
, то які корені має рівняння 


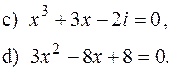
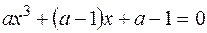 має кратний корінь? Знайти його.
має кратний корінь? Знайти його. ?
? , коли відомо, що серед його коренів є два числа, обернених за абсолютною величиною і протилежних за знаком.
, коли відомо, що серед його коренів є два числа, обернених за абсолютною величиною і протилежних за знаком. , коли відомо, що добуток двох його коренів дорівнює 1.
, коли відомо, що добуток двох його коренів дорівнює 1. , коли відомо, що його коефіцієнти в порядку спадання степенів утворюють геометричну прогресію з знаменником 2.
, коли відомо, що його коефіцієнти в порядку спадання степенів утворюють геометричну прогресію з знаменником 2. ?
? – це …
– це … , зростаючи, проходить через корінь якої-небудь проміжної функції ряду, але не проходить через корінь
, зростаючи, проходить через корінь якої-небудь проміжної функції ряду, але не проходить через корінь 


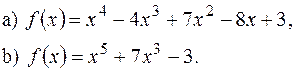
 на проміжку [0,2],
на проміжку [0,2],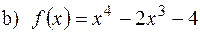 на проміжку [-3,5].
на проміжку [-3,5].