
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розділ IV. Многочлени над полем раціональних чисел таСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Алгебраїчні числа Цілі і раціональні корені многочлена з цілими коефіцієнтами. Критерій незвідності Ейзенштейна.
Будь-яке алгебраїчне рівняння з раціональними коефіцієнтами можна звести до рівняння з цілими коефіцієнтами множенням на спільний знаменник усіх цих коефіцієнтів.
Теорема 1. Щоб число Наслідок. Якщо старший коефіцієнт рівняння з цілими коефіцієнтами рівний 1, то всі раціональні корені цього рівняння є цілі числа і є дільниками вільного члена.
Теорема 2 Щоб дріб
· Ця умова використовується частіше для
Наслідок. Якщо старший коефіцієнт Теорема 3. Для того, щоб многочлен Теорема 4. У кільці многочленів над полем раціональних чисел є многочлени довільного степеня, незвідні у полі Q. Теорема 5. Якщо многочлен Теорема 6. Якщо многочлен третього степеня
Теорема 7. (Критерій Ейзенштейна незвідності многочлена з цілими коефіцієнтами): Якщо в многочлені з цілими коефіцієнтами
ПРИКЛАДИ РОЗВ’ЯЗУВАННЯ ЗАДАЧ. 12.1. Розв¢зати рівняння Розв’язання. Знайдемо спочатку раціональні корені рівняння (якщо вони є). Раціональними коренями тут можуть бути числа виду: Знайдемо межі дійсних коренів даного рівняння:
Всі можливі корені входять в цей інтервал. Знаходимо: Поставимо умову, щоб числа
Задовольняє умову
Отже, корені 12.2. Знайти раціональні корені: Розв’язання. Робимо заміну:
Повертаємось до змінної
Раціональними коренями рівняння (1) можуть бути числа
12.3. Розкласти на незвідні у полі Розв’язання.
12.4. Знайти кратність коренів многочлена
Розв’язання. Коренями можуть бути числа Скористаємося схемою Горнера:
Як бачимо рівняння має три кореня: а -1- це корінь кратності 1.
§ 13. Алгебраїчні і трансцендентні числа. Нехай Означення 1. Число α називається алгебраїчним відносно поля Р, якщо воно є коренем деякого многочлена над полем Число, яке не є алгебраїчним відносно поля Означення 2. Якщо α є алгебраїчним числом відносно поля Означення 3. Мінімальним полем Означення 4. Поле Теорема 1. Поле Наслідок. Якщо α - корінь многочлена другого степеня над полем Означення 5. Якщо корінь α квадратного тричлена над полем Поля Р. Означення 6. Розширення Теорема 2. Просте алгебраїчне розширенням Наслідок. Степінь будь-якого квадратичного розширення числового поля рівне 2. Означення 7. Розширення Означення 8. Розширення
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 805; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.208.243 (0.022 с.) |

 , де (
, де ( ) = 1 було коренем рівняння з цілими коефіцієнтами необхідно, щоб
) = 1 було коренем рівняння з цілими коефіцієнтами необхідно, щоб  було дільником вільного члена многочлена
було дільником вільного члена многочлена  , а
, а  - дільником старшого коефіцієнта цього рівняння.
- дільником старшого коефіцієнта цього рівняння. , необхідно, щоб при довільному цілому
, необхідно, щоб при довільному цілому 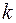 число
число  ділилося на
ділилося на  , де
, де  0.
0. 1, при цьому числа
1, при цьому числа  і
і  мають бути цілими.
мають бути цілими. многочлена
многочлена  з цілими коефіцієнтами рівний 1, то його раціональними коренями можуть бути лише такі цілі числа
з цілими коефіцієнтами рівний 1, то його раціональними коренями можуть бути лише такі цілі числа  ) при будь-якому
) при будь-якому  і
і  ненульового степеня з цілими коефіцієнтами такі, що
ненульового степеня з цілими коефіцієнтами такі, що  .
. , то
, то  діляться на деяке просте число
діляться на деяке просте число  не ділиться на
не ділиться на  , а старший коефіцієнт
, а старший коефіцієнт  .
.
 .
. .
. були цілими:
були цілими: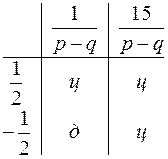
 . Перевіримо за схемою Горнера чи є це коренем даного рівняння:
. Перевіримо за схемою Горнера чи є це коренем даного рівняння: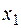 = 1/2 є коренем многочлена. Знаходимо інші корені:
= 1/2 є коренем многочлена. Знаходимо інші корені:
 .
. .
.

 . Маємо два рівняння:
. Маємо два рівняння: (1) або
(1) або (2)
(2)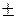 1, а рівняння (2):
1, а рівняння (2): 
 множники многочлен
множники многочлен  .
. .
.
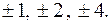
 Корені 1 і -2 мають кратність 2,
Корені 1 і -2 мають кратність 2, – деяке числове поле.
– деяке числове поле. існує єдиний незвідний зведений (
існує єдиний незвідний зведений (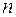 є найменшим серед степенів усіх многочленів з коренем α.
є найменшим серед степенів усіх многочленів з коренем α. , утворене приєднанням до поля
, утворене приєднанням до поля  , складається з усіх чисел виду
, складається з усіх чисел виду  , де
, де  - довільні числа з поля
- довільні числа з поля  , причому
, причому  , то просте алгебраїчне розширенням
, то просте алгебраїчне розширенням  , де
, де  і
і  – довільні числа з поля
– довільні числа з поля  поля
поля  , що будь-який елемент
, що будь-який елемент  є лінійною комбінацією цих елементів з коефіцієнтами з поля
є лінійною комбінацією цих елементів з коефіцієнтами з поля  . Система
. Система 
 - базис поля
- базис поля  , що
, що  , причому кожне
, причому кожне  (при
(при  ).
).


