
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Раціональні дроби. Елементарні дроби. Розклад дробу на елементарні дроби надполями q,r і C.Содержание книги
Поиск на нашем сайте
Теорема 1. Для будь-якого поля Означення 1. Раціональний дріб Приклад: (Далі всі дроби вважати раціональними) Лема 1. Сума правильних дробів є правильний дріб. Означення 2. Елементарним дробом у полі Р називається раціональний дріб виду полі Кожен елементарний дріб є правильним.
Лема 2. Якщо Наслідок. Якщо Лема 3. Всякий правильний дріб над полем Наслідок. Кожен правильний дріб над полем
Теорема 2. Всякий правильний дріб над полем Теорема 3. Розклад правильного раціонального дробу на елементарні дроби у даному полі єдиний. Теорема 4. Всякий неправильний дріб Нехай Р – деяке поле, Шуканий многочлен має вигляд
Многочлен (1) називають інтерполяційним многочленом Лагранжа. Іноді доцільно многочлен
де коефіцієнти Многочлен (2) називають інтерполяційним многочленом Ньютона.
ПРИКЛАДИ РОЗВ’ЯЗУВАННЯ ЗАДАЧ.
4.1. Використовуючи інтерполяційну формулу Ньютона побудувати многочлен найменшого степеня
Розв’язання. Щоб знайти коефіцієнти многочлена
В нашому випадку многочлен набуде такого вигляду: Підставивши вцей вираз значення
Тому маємо:
4.2. У полі
Розв’язання. а) Розкладемо чисельник і знаменник на прості множники і маємо:
б)
Розділимо
x8 + x4 + 1 | x2 + x + 1 x8 + x7 + x6 | x6 - x5 + x3 - x + 1 -x7 - x6 + x4 + 1 - x7 - x6 - x5 x5 + x4 + 1 x5 + x4 + x3 -x3 + 1 -x3 - x2 - x x2 + x + 1 x2 + x + 1
4.3. Перевірити, чи є раціональний дріб полем Розв’язання. Нагадаємо, що
4.4. Розкласти дріб на елементарні дроби:
Розв’язання. Цей дріб нескоротний, бо НСД чисельника і знаменника дорівнює 1. Розкладемо знаменник на незвідні множники над R і, використовуючи метод невизначених коефіцієнтів, леми 2, 3 та наслідки з них маємо:
Прирівняємо відповідні коефіцієнти:
маємо:
б)
Розв’язання. Розкладемо знаменник дробу на незвідні над Q многочлени:
в)
Розв’язання.
Розкладемо знаменник дробу на незвідні над С многочлени:
4.5. Довести тотожність: де Розв’язання. Розглянемо многочлен
Обчислимо його значення, якщо Це значить, що многочлен Як відомо, над полем R існує лише один многочлен, степінь якого не більша 2 і який при трьох різних дійсних числах
Розділ II. Многочлени від кількох змінних
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 1486; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.42.247 (0.007 с.) |

 існує єдине поле
існує єдине поле 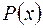 , яке містить кільце
, яке містить кільце  многочленів над полем
многочленів над полем  , де
, де  .
. менша за степінь многочлена
менша за степінь многочлена  . В іншому разі дріб – неправильний.
. В іншому разі дріб – неправильний. - правильний дріб,
- правильний дріб,  - неправильний дріб.
- неправильний дріб. , де
, де  і
і  , а
, а 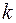 – будь-яке натуральне число.
– будь-яке натуральне число. і
і  - взаємнопрості многочлени над полем Р і
- взаємнопрості многочлени над полем Р і 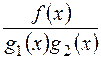 - правильний раціональний дріб над цим полем, то в кільці
- правильний раціональний дріб над цим полем, то в кільці  і
і  , що
, що  .
.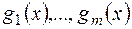 - попарно взаємно прості многочлени над полем
- попарно взаємно прості многочлени над полем  - правильний раціональний дріб над цим полем, то в кільці
- правильний раціональний дріб над цим полем, то в кільці  , що
, що  , причому всі дроби у правій частині правильні.
, причому всі дроби у правій частині правильні. , з яких перший є елементарний в полі
, з яких перший є елементарний в полі  .
. , де
, де 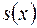 - ціла частина дробу
- ціла частина дробу  ,
,  – правильний дріб.
– правильний дріб. - різні елементи поля
- різні елементи поля  - довільні елементи поля
- довільні елементи поля  задані значення
задані значення  ,
, 
 (1)
(1) (2)
(2) визначаються послідовним підставленням значень
визначаються послідовним підставленням значень  .
. за такою таблицею:
за такою таблицею:
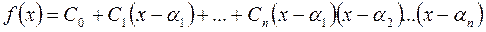 .
.
 складемо систему:
складемо систему:

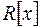 знайти нескоротний дріб, який дорівнює
знайти нескоротний дріб, який дорівнює ,
,  .
. - нескоротний дріб.
- нескоротний дріб.
 ”кутом” на
”кутом” на  :
: .
. , якщо
, якщо  .
. , де
, де  - незвідний над полем многочлен
- незвідний над полем многочлен  і
і  .
.
 ,
,  - незвідний у полі
- незвідний у полі  над
над 
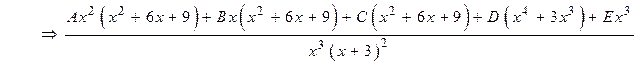

 .
. над
над  .
.

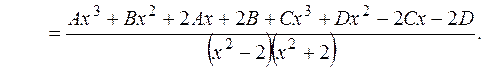

 над
над  .
.






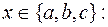
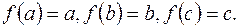
 набуває значень:
набуває значень: 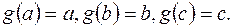
 набуває значень
набуває значень 


