
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кільце многочленів від n змінних. Розклад многочлена на добуток незвідних множників. Симетричні многочлени.Содержание книги
Поиск на нашем сайте
Означення 1. Кільцем многочленів Кільце многочленів де Означення 2. Кожний елемент кільця і т.д. Кожен доданок
Приклад:
Теорема 1. Будь-який многочлен Означення 2 Степенем члена
Приклад: 7 – степінь многочлена, Означення 3. Якщо всі члени многочлена мають однаковий степінь, то многочлен називається однорідним. Теорема 2. Якщо
Нехай Приклад:
Лема 1. Вищий член добутку двох многочленів дорівнює добутку вищих членів цих многочленів. Означення 4. Вважатимемо, що многочлен
Властивості подільності: 1) 2) 3) 4) 5) 6)
Означення 5. Многочлен Многочлен
Властивості незвідних многочленів: 1) Якщо р незвідний у полі 2) Якщо 3) Будь-який многочлен Теорема 3. Будь-який многочлен
Лема 2. Для будь-якої скінченої системи елементів Означення 6. Многочлен Лема 3. Добуток двох примітивних многочленів з Означення 7. Многочлен
Приклад:
Властивості симетричних многочленів: 1) Сума, різниця і добуток симетричних многочленів від n змінних над деяким полем Наслідок. Множина всіх симетричних многочленів від 2) Якщо симетричний многочлен 3) Якщо
Теорема 4. (основна теорема теорії симетричних Всякий симетричний многочлен
Елементарні симетричні многочлени:
Представлення симетричних сум через елементарні симетричні многочлени:
ПРИКЛАДИ РОЗВ’ЯЗУВАННЯ ЗАДАЧ. 5.1. Упорядкувати лексикографічно і знайти вищий член многочлена
Розв’язання. Маємо
Вищий член многочлена:
5.2. Застосовуючи заміну
Розв’язання. Маємо:
5.3. Чи симетричні многочлени:
Розв’язання. Нехай
Розв’язання. Нехай Нехай Нехай Цей многочлен симетричний.
5.4. Виразити через елементарні симетричні многочлени
Розв’язання.
§ 6. Застосування симетричних многочленів до розв¢язування деяких задач з елементарної алгебри.
|
||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 860; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.1.100 (0.007 с.) |

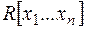 від
від 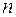 змінних
змінних  над областю цілісності R називається кільце многочленів від однієї змінної
над областю цілісності R називається кільце многочленів від однієї змінної  над кільцем
над кільцем  , тобто
, тобто  над областю цілісності R є область цілісності, причому кожен елемент
над областю цілісності R є область цілісності, причому кожен елемент  можна подати як скінчену суму:
можна подати як скінчену суму:  , (1),
, (1),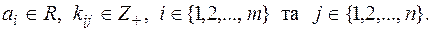
 і позначається
і позначається  ,
, 
 в сумі (1) називається членом многочлена
в сумі (1) називається членом многочлена 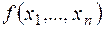 , елемент
, елемент  – коефіцієнтом цього члена. Два члени, які відрізняються тільки коефіцієнтами називаються подібними.
– коефіцієнтом цього члена. Два члени, які відрізняються тільки коефіцієнтами називаються подібними. -многочлен від двох зміннихx, y.
-многочлен від двох зміннихx, y. можна подати у канонічній формі (без подібних членів).
можна подати у канонічній формі (без подібних членів). многочлена називається сума
многочлена називається сума  . Число
. Число  називається степенем даного члена відносно
називається степенем даного члена відносно  . Найбільший із степенів членів називається степенем многочлена, а член з найбільшим степенем – старшим членом многочлена.
. Найбільший із степенів членів називається степенем многочлена, а член з найбільшим степенем – старшим членом многочлена.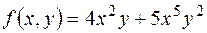
 - старший член многочлена.
- старший член многочлена. .
. - два члени многочлена
- два члени многочлена  . Відношення “бути вищим” на множині членів многочленів є лінійним строгим порядком, його називають лексикографічним (позначають
. Відношення “бути вищим” на множині членів многочленів є лінійним строгим порядком, його називають лексикографічним (позначають 
 - лексикографічний запис многочлена,
- лексикографічний запис многочлена,  - вищий член.
- вищий член. ділиться на многочлен
ділиться на многочлен  і записуватимемо
і записуватимемо 

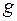 , якщо існує такий многочлен
, якщо існує такий многочлен 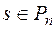 , що
, що 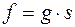 . При цьому
. При цьому 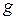 - дільник
- дільник 

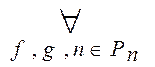











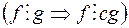
 називається незвідним у
називається незвідним у  і
і  .
.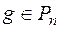 називається звідним у полі Р, якщо
називається звідним у полі Р, якщо 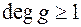 і
і  .
. многочлен, то і будь-який асоційований з ним многочлен
многочлен, то і будь-який асоційований з ним многочлен  незвідний у полі
незвідний у полі  і
і  незвідні у полі Р многочлени і
незвідні у полі Р многочлени і  , то
, то  першого степеня незвідний у полі
першого степеня незвідний у полі 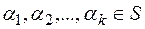 (
( – область цілісності), відмінних від нуля, існує єдиний (з точністю до дільників одиниці) НСД.
– область цілісності), відмінних від нуля, існує єдиний (з точністю до дільників одиниці) НСД. називається примітивним (відносно
називається примітивним (відносно  є примітивний многочлен.
є примітивний многочлен. називається симетричним відносно змінних
називається симетричним відносно змінних  , якщо внаслідок довільної перестановки змінних
, якщо внаслідок довільної перестановки змінних  симетричний відносно
симетричний відносно  ;
; симетричний відносно
симетричний відносно  , але несиметричний відносно
, але несиметричний відносно  або
або 
 не симетричний відносно
не симетричний відносно 
 , то він містить і член, утворений з даного, внаслідок будь-якої перестановки показників
, то він містить і член, утворений з даного, внаслідок будь-якої перестановки показників 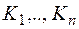 .
. .
. цих змінних, коефіцієнти якого належать тому ж полю
цих змінних, коефіцієнти якого належать тому ж полю 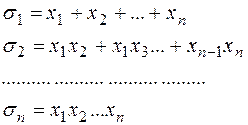

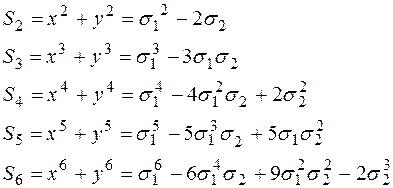

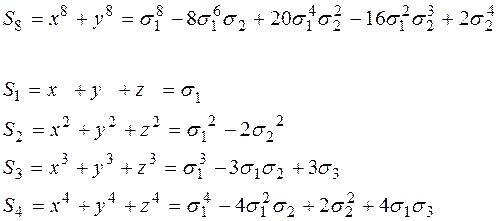
 з кільця
з кільця  .
.
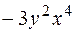 . Многочлен впорядковано за спаданням степенів
. Многочлен впорядковано за спаданням степенів  .
.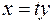 розкласти на незвідні у полі
розкласти на незвідні у полі 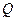 многочлен
многочлен  .
.
 .
.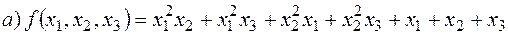 .
.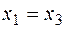 , тоді
, тоді 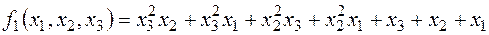 ,
, цей многочлен несиметричний.
цей многочлен несиметричний. .
. , тоді
, тоді 
 , тоді
, тоді 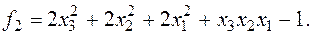
 , тоді
, тоді 
 .
.



