
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Многочлени над полем комплексних чисел. Алгебраїчна замкненість поля комплексних чисел.Содержание книги
Поиск на нашем сайте
Нехай Поле
Теорема 1. Многочлен непарного степеня над полем Теорема 2. Кожний многочлен степеня Теорема 3. (Основна теорема теорії многочленів): Довільний многочлен ненульового степеня з комплексними коефіцієнтами Теорема 4. Кожний многочлен, степінь якого вища за одиницю, звідний у полі комплексних чисел. Наслідок. Для того, щоб многочлен був незвідним у полі комплексних чисел, необхідно і достатньо, щоб його степінь дорівнював 1.
Теорема 5. Кожний многочлен
де Терема 6. Многочлен
Очевидно, що всі корені многочлена
..........................................
ПРИКЛАДИ РОЗВ’ЯЗУВАННЯ ЗАДАЧ. 8.1. Знайти многочлен найменшого степеня, в якого число 2 - подвійний корінь, а
Розв’язання. Могочлен
8.2. Знайти суму кубів коренів многочлена
Розв’язання. Нехай
8.3. Знайти зведені многочлени, в яких корені задовольняють умову:
Розв’язання. Запишемо многочлен
За теоремою Вієта при умові, що
Отримаємо:
8.4. Розкласти на незвідні множники многочлен Розв’язання. Знайдемо корені многочлена
Тоді маємо, що 8.5. Знайти суму кубів коренів многочлена Розв’язання. За теоремою Вієта маємо: Тоді 8.6. Корені многочлена Розв’язання. Нехай
За теоремою Вієта маємо:
Складемо систему: Розв¢язавши її отримаємо такі значення: Отже, Многочлени над полем дійсних чисел. Нехай (1)
Теорема 1. Якщо комплексне число Теорема 2. Якщо комплексне число Теорема 3. Кожний многочлен над полем Теорема 4. Кожний многочлен над полем
ПРИКЛАДИ РОЗВ’ЯЗУВАННЯ ЗАДАЧ. 9.1. Розв’язати рівняння
Розв’язання. Задане рівняння має дійсні коефіцієнти, тому число (наслідок з теореми Безу). Виконаємо ділення ”кутом”:
x4 - x3 - 11x2 + 31x - 20 | x2 - 4x + 5 x4 - 4x3 + 5x2 | x2 + 3x - 4 3x3 - 16x2 + 31x 3x3 - 12x2 + 15x _-4x2 + 16x - 20 -4x2 + 16x - 20 Щоб знайти інші корені заданого рівняння розв’яжемо рівняння Корені: 9.2. Число Розв’язання. Маємо
x3 + x2 + ax + b | x2 + 6x + 10 x3 + 6x2 + 10x | x - 5 -5x2 + (a - 10)x + b -5x2 - 30x - 50 (a + 20)x + (b + 50) = Щоб
Тоді Рівняння третього степеня. Нехай
Число Якщо Числа
Якщо коефіцієнти p i q рівняння (1) є дійсними числами, то: 1) при 2) при 3) при
|
||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 1473; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.006 с.) |

 - деякий многочлен над полем
- деякий многочлен над полем  . Якщо
. Якщо 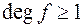 , то існує розширення
, то існує розширення 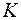 поля
поля 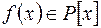 степеня
степеня  поля
поля  у вигляді добутку лінійних множників.
у вигляді добутку лінійних множників. називається полем розкладу многочлена
називається полем розкладу многочлена  на лінійні множники. Поле
на лінійні множники. Поле  дійсних чисел має принаймні один дійсний корінь.
дійсних чисел має принаймні один дійсний корінь. з дійсними коефіцієнтами має принаймні один комплексний корінь.
з дійсними коефіцієнтами має принаймні один комплексний корінь.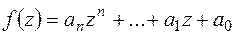 має хоча б один комплексний корінь.
має хоча б один комплексний корінь.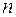 -го степеня у полі комплексних чисел єдиним чином (з точністю до порядку множників) розкладається на лінійні множники у цьому полі:
-го степеня у полі комплексних чисел єдиним чином (з точністю до порядку множників) розкладається на лінійні множники у цьому полі: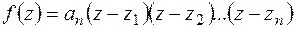 ,
, - корені,
- корені,  - старший коефіцієнт
- старший коефіцієнт 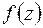 над полем комплексних чисел належать цьому ж полю, тобто полем розкладу будь-якого многочлена
над полем комплексних чисел належать цьому ж полю, тобто полем розкладу будь-якого многочлена 
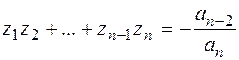

 – прості.
– прості.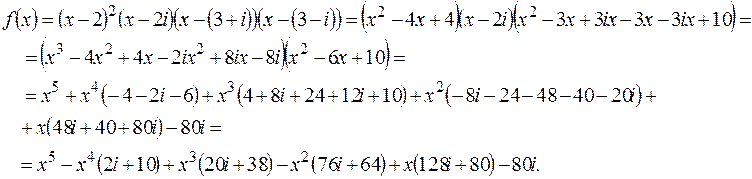
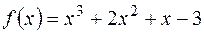
 – корені многочлена
– корені многочлена 

 , а
, а  є коренями многочлена
є коренями многочлена  .
.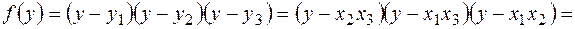
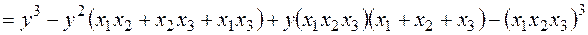 .
.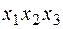 - корені
- корені 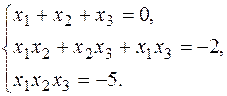
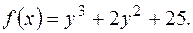
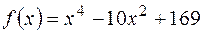 .
. .
.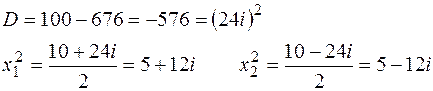
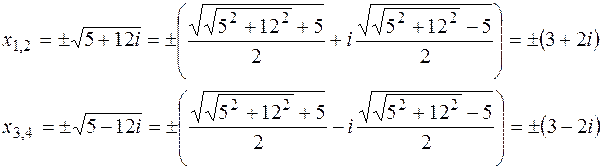

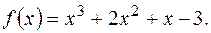


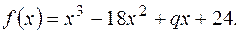
 -корені многочлена
-корені многочлена 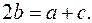
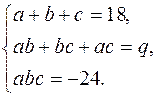
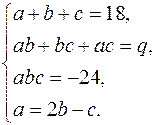
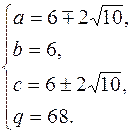

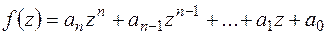 - многочлен з дійсними коефіцієнтами.
- многочлен з дійсними коефіцієнтами. - є коренем многочлена (1), то спряжене комплексне число
- є коренем многочлена (1), то спряжене комплексне число 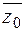 є коренем цього ж многочлена.
є коренем цього ж многочлена.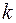 -ї кратності многочлена
-ї кратності многочлена 
 , якщо
, якщо  .
. теж є коренем, а многочлен ділиться на
теж є коренем, а многочлен ділиться на 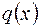 :
: 
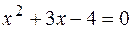 .
. .Тому
.Тому 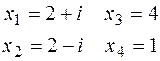
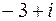 є коренем рівняння з дійсними коефіцієнтами
є коренем рівняння з дійсними коефіцієнтами  . Знайти
. Знайти  та два інші корені.
та два інші корені. , а тому
, а тому 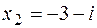 - теж корінь (див. вище).Тоді многочлен
- теж корінь (див. вище).Тоді многочлен 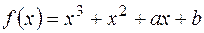 поділимо на
поділимо на  :
: 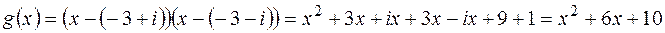 .
.
 необхідно і достатньо, щоб
необхідно і достатньо, щоб 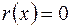 :
: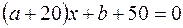 ,
, 
 0 тому
0 тому 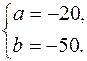 .
.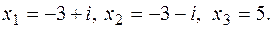
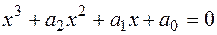 - рівняння третього степеня з комплексними коефіцієнтами. За допомогою підстановки
- рівняння третього степеня з комплексними коефіцієнтами. За допомогою підстановки 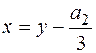 зведемо його до виду
зведемо його до виду  (1)
(1)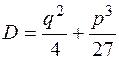 називають дискримінантом рівняння (1). Корені цього рівняння знаходять за формулою
називають дискримінантом рівняння (1). Корені цього рівняння знаходять за формулою  , яка називається формулою Кардано.
, яка називається формулою Кардано.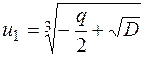 і
і 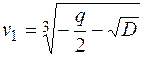 є тими значеннями кубічних коренів, при яких
є тими значеннями кубічних коренів, при яких 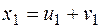 є коренями рівняння (1), то решту коренів цього рівняння обчислюють так:
є коренями рівняння (1), то решту коренів цього рівняння обчислюють так: 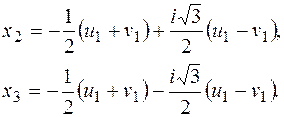
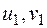 знаходяться з умови
знаходяться з умови 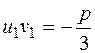 .
. рівняння має один дійсний корінь і два комплексних спряжених корені;
рівняння має один дійсний корінь і два комплексних спряжених корені; рівняння має три дійсних корені і два з яких дорівнюють один одному;
рівняння має три дійсних корені і два з яких дорівнюють один одному;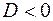 рівняння має три дійсних різних корені.
рівняння має три дійсних різних корені.


