
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кільце многочленів. Алгебраїчна і функціональна рівність многочленів. Відношення подільності в кільці многочленів. Ділення з остачею.Содержание книги
Поиск на нашем сайте
Означення 1. Многочленом (поліномом) від однієї змінної над областю цілісності R називається вираз виду:
Приклад:
Означення 2. Область цілісності – це комутативне кільце з 1 без дільників нуля (R[x] - сукупність всіх многочленів над областю цілісності). Означення 3. Вираз Якщо Означення 4. Відмінний від нуля член многочлена
З попереднього прикладу: 5 4 – степінь многочлена. Степінь
Означення 5. Елемент 0 Означення 6. Канонічною формою многочлена
Приклад:
Означення 7. Сумою многочленів
Наслідок 1. Степінь суми двох многочленів не перевищує більшого з степенів даних многочленів: deg ( Наслідок 2. Для довільного многочлена
Означення 8. Добутком многочленів
Наслідок 3. Якщо deg ( Наслідок 4. Якщо Означення 9. Якщо многочлен Якщо Означення 10. Многочлени Означення 11. Кожен многочлен
Якщо область цілісності R має характеристику 0, то многочлени
Алгебраїчне і функціональне тлумачення многочленів рівносильні над областю цілісності характеристики 0.
Якщо многочлени рівні алгебраїчно, то очевидно вони рівні і функціонально. Обернене твердження не виконується.
Означення 12. Нехай Р- деяке поле. Многочлен
Відношення подільності многочленів над полем Р має такі властивості: 1) 2) 3) 4) 5) 6) 7) Þ Означення 13. У кільці Р[x] многочлени
Теорема 1. Довільний многочлен
Для знаходження частки і остачі від ділення многочлена
ПРИКЛАДИ РОЗВ’ЯЗУВАННЯ ЗАДАЧ.
Розв’язання. Многочлен
Так як ці многочлени рівні, то маємо систему рівнянь:
З першого і останнього рівнянь системи знаходимо, що
Отже, при
1.2. Довести, що з функціональної точки зору наступні многочлени дорівнюють один одному:
Розв’язання.
З функціональної точки зору многочлени рівні, якщо рівні між собою функції jf і jg , які вони визначають, тобто, якщо функції набувають однакових значень при однакових лишках:
Отже,
1.3. Знайти суму коефіцієнтів многочлена: Розв’язання. Сума коефіцієнтів дорівнює значенню многочлена при
1.4. Знайти остачу від ділення Розв’язання. Для многочленів
Тому можемо записати таку рівність:
Враховуючи, що g (-1) = g (1) = 0, то підставивши ці значення замість
Тому 1.5. Остачі від ділення многочленів Розв’язання. За теоремою про ділення з остачею маємо: Запишемо умову задачі згідно цих розкладів: Звідси маємо, що шукана остача § 2. Ділення многочлена на двочлен (x-a). Теорема Безу. Схема Горнера. Розклад многочлена за степенями (x-a). Найбільший спільний дільник і найменше спільне кратне многочленів. Алгоритм Евкліда. Теорема Безу. Для будь-якого елемента a з поля Р остача при діленні многочлена Наслідок. Якщо Приклад.1 Поділити многочлен на двочлен (
_4x4 + x3 - ділене | x + 1 + i - дільник 4x4 + (4 + 4i) x3 |4x3 – (3 + 4i) x2 + (7i - 1) x + 8 – 6i = _-(3 + 4i) x3 -(3 + 4i) x3 – (1+ i)(3 + 4i) x2 _(7i - 1) x2 2. Метод невизначених коефіцієнтів: 4 тому
4 маємо:
тому
3. Схема Горнера: a = -1 - i
При кожному наступному діленні старший коефіцієнт переписується, а робочою стрічкою стає щойно написана стрічка з коефіцієнтів.
Розкласти многочлен за степенями (x - a) означає представити його у вигляді: Це зручно робити за схемою Горнера, де с0, с1,..., сn являються частками при послідовному діленні многочлена Приклад: Розкласти многочлен ( Розв’язання. Виконаємо послідовне ділення многочлена
Маємо
Означення 1. Якщо многочлен Означення 2. Спільний дільник многочленів Означення 3. Многочлени Теорема 2. Для будь-яких двох многочленів Таке представлення називається лінійним представленням НСД, де Наслідок. Многочлени
Властивості взаємно простих многочленів: 1) 2) 3) Алгоритм Евкліда.
Маємо
…
Остання відмінна від нуля остача у цій системі рівностей
Властивості НСД: 1) будь-які многочлени 2) якщо 3) якщо
Зауваження: НСД можна обчислювати з точністю до сталого множника. Приклад: Знайти НСД
Розв’язання. 1) ( x4 + x3 + x2 + x + 1 | 5x3 + 4x2 + 3x + 2 _5x4 + 5x3 + 5x2 + 5x + 5 |x + 1 = 5x4 + 4x3 + 3x2 + 2x x3 + 2x2 + 3x + 5 _5x3 + 10x2 + 15x + 25 5x3 + 4x2 + 3x + 2 6x2 + 12x + 23 =
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

 , де
, де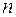 - довільне ціле невід’ємне число,
- довільне ціле невід’ємне число, – елементи R,
– елементи R, – деякі символи;
– деякі символи; - k-ий степінь змінної
- k-ий степінь змінної  ,
, - k-ий коефіцієнт многочлена або коефіцієнт при
- k-ий коефіцієнт многочлена або коефіцієнт при  (k=
(k= 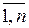 ).
).

 (k =
(k =  ) називається k-тим
) називається k-тим  - нульовим або вільним членом.
- нульовим або вільним членом. (тобто є нульовим елементом області цілісності R), то кажуть, що k-тий член многочлена
(тобто є нульовим елементом області цілісності R), то кажуть, що k-тий член многочлена  дорівнює нулю або його немає.
дорівнює нулю або його немає. – старший член, 5 – старший коефіцієнт,
– старший член, 5 – старший коефіцієнт, R вважаємо константою і многочленом над R. Його називають нуль-многочленом, і позначають
R вважаємо константою і многочленом над R. Його називають нуль-многочленом, і позначають  , тобто
, тобто 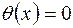 .
. - канонічна форма, а
- канонічна форма, а - не канонічна форма запису многочлена.
- не канонічна форма запису многочлена. називають многочлен
називають многочлен ,
, ) ≤ max (deg
) ≤ max (deg 

 , де
, де  ,
, 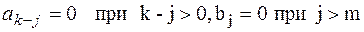 , тобто
, тобто 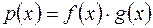 .
. R[x], має канонічну форму, i
R[x], має канонічну форму, i  , то елемент
, то елемент 
 з
з  при
при 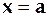 і
і  .
. , то число
, то число  називається коренем
називається коренем  .
.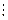

 [
[ 
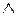
 Þ
Þ  [
[ 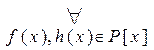 [
[ 
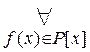
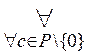 [
[  [
[ 

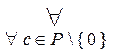 [
[  [
[ 
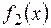

 …
… 
 [(
[(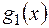 + … +
+ … + 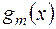 )
)  .
. належать Р[x] і визначаються однозначно, тобто
належать Р[x] і визначаються однозначно, тобто , причому
, причому  або deg
або deg  , при яких многочлен
, при яких многочлен  є квадратом деякого многочлена
є квадратом деякого многочлена  з кільця
з кільця  , та записати многочлен
, та записати многочлен 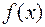 має степінь 4. Тому степінь шуканого многочленна
має степінь 4. Тому степінь шуканого многочленна і
і 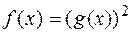 . Запишемо многочлен
. Запишемо многочлен 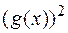 у канонічній формі:
у канонічній формі: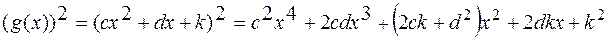 .
.
 .Це означає, що система рівна сукупності чотирьох систем:
.Це означає, що система рівна сукупності чотирьох систем: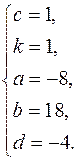


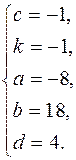
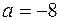 і
і  многочлени
многочлени  і
і  мають вигляд:
мають вигляд: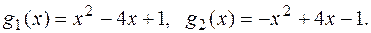 При
При 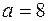 і
і  отримуємо такі многочлени:
отримуємо такі многочлени: 
 з кільця
з кільця  .
.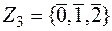 - остачі від ділення на 3 (лишки за модулем 3).
- остачі від ділення на 3 (лишки за модулем 3).





 у кільці
у кільці  .
.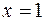 .
.
 на
на  у кільці Z[x].
у кільці Z[x].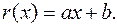
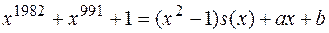 .
.
 на
на  в кільці Q[x] відповідно дорівнюють
в кільці Q[x] відповідно дорівнюють  ,
,  Знайти остачу від ділення многочлена
Знайти остачу від ділення многочлена  на g (x).
на g (x).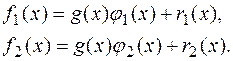


 .
. (a).
(a). = a є коренем
= a є коренем  (
( – a) можна “кутом”:
– a) можна “кутом”:
 3, deg
3, deg 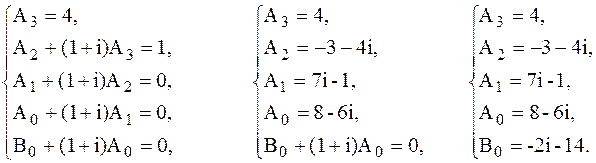

 4
4

 1
1

 0
0

 0
0
 0
0




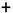 4
4

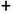
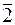
 =
=  в кільці Z3[
в кільці Z3[  ), використовуючи схему Горнера.
), використовуючи схему Горнера.


 =
=  =
=  )4 + (
)4 + (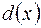 є дільником многочлена
є дільником многочлена  .
. +
+ 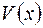 .
.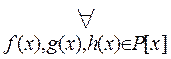 [(
[(
 [
[ 
 [
[ 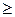 deg
deg 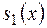 +
+ 
 +
+ 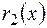
 +
+ 
 =
= 
 +
+ 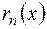

 0 і
0 і 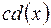 – теж НСД многочленів
– теж НСД многочленів  - НСД многочленів
- НСД многочленів 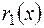 – остача
– остача


