
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Зразок розв’язання контрольної роботи № 1Содержание книги Поиск на нашем сайте
Варіант 0. 1. Довести, що множина
відносно множення підстановок є групою.
Розв‘язок. Під множенням підстановок розуміють їх послідовне виконання. Необхідно показати, що множина G: 1) замкнена відносно операції (×); 2) виконується для елементів множини асоціативний закон множення; 3) існує нейтральний елемент відносно цієї операції; 4) кожний елемент множини має обернений. Складаємо таблицю Келі для операції (×) на множині G.
Операцію (×) задано так:
За таблицею видно, що всі групові властивості виконуються на множині відносно заданої на ній операції (×). Отже, G – група. Вона називається симетричною групою третього степеня (S 3). 2) Знайти всі твірні елементи групи S 3. Розв‘язок. Група S 3 є групою 6-го порядку. Отже, всі її елементи мають скінчений порядок, який за теоремою Лагранжа є дільником порядку групи. Отже, в групі S 3 є елементи другого та третього порядків. Елементи s 2, s 3 – елементи третього порядку, так як (s 2)3 = (s 3)3 = s 1. Елементи s 4, s 5, s 6 – елементи другого порядку, так як (s 4)2 = (s 5)2 = (s 6)2 = s 1. Отже, група S 3 – це неабелева група і породжується відповідно елементом порядку 3 і елементом порядку 2, тобто S 3 = { s 2, s 4} = { s 2, s 5} = { s 2, s 6} = { s 3, s 5} = { s 3, s 4} = { s 3, s 6}. 3) Знайти всі підгрупи групи S 3. Розв‘язок. За теоремою Лагранжа порядок підгрупи є дільником порядку групи. Тому група S 3 може мати власні підгрупи порядків 3 та 2 і невласні підгрупи: E, S 3. Підгрупою 3-го порядку є підмножина групи S 3, що складається із елементів < s 1, s 2, s 3> і підгрупами 2-ого порядку є підмножини групи S 3, що складаються із елементів < s 1, s 4>, < s 1, s 5>, < s 1, s 6>. Підгрупа G 1 = < s 1, s 2, s 3> = { s 2} = { s 3}; G 2 = < s 1, s 3> = { s 3}; G 3 = < s 1, s 5> = { s 5}; G 4 = < s 1, s 6> = { s 6}. Отже, будь-яка власна підгрупа групи S 3 – циклічна, тобто складається із степенів одного із своїх (твірного) елементів. 3. Розкласти групу S 3 на класи спряжених елементів. Розв‘язок. Оскільки s 1 утворює окремий клас спряжених елементів як одиниця групи S 3; елементи s 2, s 3 порядку 3 утворюють клас спряжених елементів, так як si –1× s 3× si = s 2, si –1× s 2× si = s 3;
елементи s 4, s 5, s 6 порядку 2 спряжені, так як s 5 s 4 s 5 = s 6, s 6 s 5 s 6 = s 4, s 4 s 5 s 4 = s 6, а тому належать одному класу спряжених елементів. Отже, S 3 = < s 1> + < s 2, s 3> + < s 4, s 5, s 6 >. 4. Розкласти групу S 3 на ліві суміжні класи за її підгрупою G 2 = < s 1, s 6>. Розв‘язок. Лівосторонній розклад групи S 3 за її підгрупою G 2 складається із класів: G 2, s 2 G 2 = s 4 G 2 = { s 2, s 4}, s 5 G 2 = s 6 G 2 = { s 4, s 6}. S 3 = G 2 È{ s 2, s 4}È{ s 4, s 6}. 5. Знайти нормальний дільник в групі S 3. Розв‘язок. Для того, щоб підгрупа групи була її нормальним дільником необхідно і достатньо, щоб ліві і праві суміжні класи за цією підгрупою співпадали. Отже, в симетричній групі S 3 підгрупа G 1 = < s 1, s 2, s 3> є нормальним дільником групи, так як лівосторонні і правосторонні розклади групи S 3 за підгрупою G 1 співпадають: кожен з них складається з двох класів: G 1 i < s 4, s 5, s 6>, S 3 = G 1È G 1 s 4 = s 4 G 1 = { s 4, s 5, s 6}. 6. Побудувати фактор-групу групи S 3 за підгрупою G 1. Розв‘язок. Сукупність суміжних класів групи S 3 за її нормальною підгрупою G 1 відносно операції множення класів утворює групу, яка називається фактор-групою групи S 3 за підгрупою G 1 (S 3/ G 1). На множині класів введемо операцію множення siG 1× sjs 1 = si × sjs 1, si, sj Î S 3, s 1 – нормальна підгрупа. Доведемо, що одержалася група. 7. Асоціативність множення класів випливає з асоціативності множення в групі S 3: (siG 1× sjs 1)× skG 1= (sisj) s 1× skG 1 = (sisj)× skG 1= si (sj × sk) G 1 = = siG 1×(sj × sk) G 1= siG 1×(sjG 1× skG 1) 8. Одиничним елементом є сама підгрупа G 1: G 1× siG 1= s 1 G 1 ×siG 1 = s 1 siG 1 = siG 1, siG 1 ×G 1 = siG 1 ×s 1 G 1 = sis 1 G 1 = siG 1. 9. Оберненим до класу siG 1 є клас si –1 G 1, так як siG 1× si –1 G 1 = si × si –1 G 1 = eG 1 = G 1, si –1 G 1× siG 1 = si –1× siG 1 = eG 1 = G 1. Одержана група позначається через S 3/ G 1 і називається фактор-групою групи S 3 за нормальною підгрупою G 1. S 3/ G 1 = < G 1, s 4 G 1>. 10. Довести, якщо | a | = n і ak = 1, то n ділить k. Розв‘язок. Нехай порядок елемента а групи G дорівнює n. Це означає, що n – мінімальне натуральне число таке, що an = 1. Якщо k – будь-яке ціле число, то поділимо k на n, одержуємо k = nq + r, 0 £ r < n, а тому ak = (an) q × ar = ar. Звідси випливає, якщо елемент а має скінчений порядок n і ak = 1, то n ділить k. 8. Довести, якщо | G | = pq, p ¹ q – прості числа, то в G існує інваріантна підгрупа.
Розв‘язок. Нехай p, q – прості числа,. Силовські p - і q -підгрупи групи G, будучи підгрупами простого порядку, є циклічними. Нехай { a }, { b }– відповідно силовські p - і q- підгрупи. за теоремою Силова кількість силовських підгруп в G дорівнює 1 + kq і ділить pq, тому силовська q -підгрупа { b } єдина. Зокрема, вона нормальна в групі G, що і треба було довести. 9. Нехай К 1 – підкільце кільця К, І – ідеал кільця К. Довести, що К 1Ç I – ідеал кільця К. Розв‘язок. Позначимо D = К 1Ç I. Покажемо, що ідеал І, як і будь-який ідеал, містить нуль-елемент кільця К. Оскільки І ¹0, то в І існує хоч один елемент а. Тоді за означенням ідеалу, елемент а – а = 0 теж належить ідеалу I. Оскільки 0Î К, 0Î І, то 0Î D, тому D ¹Æ. Якщо а, b Î D, то а, b Î К і а, b Î І. Згідно з означенням ідеалу і критерієм підкільця Нехай а Î D, b Î К 1. Покажемо, що ab і ba належать D. Оскільки D Í І, а І – ідеал кільця К, то для будь-якого елемента а Î D Í І і будь-якого елемента b Î К 1 Í K маємо, що ab, ba Î І. Отже, ab, ba Î К 1Ç I = D. Тому D = К 1Ç I – ідеал кільця К 1. 10. Довести, що при гомоморфізмі j двох кілець K 1 і K 2 j(a – b) = j(a) – j(b). Розв‘язок. Нехай j – гомоморфізм кільця K 1 на кільце K 2. Тоді за означенням гомоморфізму виконується рівність " a, (– b)Î К 1 j(a + (– b) = j(a) + j(– b), j(– b) = – j(b). Отже, j(a + (– b) = j(a – b) = j(a) – j(b), що і треба було довести. 11. Довести, що характеристикою області цілісності є або нуль, або просте число. Розв‘язок. Нехай К – область цілісності, а е – одиниця кільця К. Якщо для me ¹0 жодного натурального числа m, то характеристика кільця К дорівнює нулю. Нехай me =0 і m – найменше натуральне число, що має цю властивість, тобто m – характеристика кільця К. Тоді m ¹1, оскільки е ¹0. Якщо m – просте число, то твердження задачі доведено. Нехай m – складене число. Тоді існують натуральні числа s і t такі, що 1 < s, t < m і m = st. Так як кільце K комутативне, маємо 0 = me = (st) × e = (se) × (te). Крім того, оскільки m – характеристика кільця К і s < m, t < m, то se ¹0, te ¹0, і тому (se) × (te) = me ¹0, бо К як область цілісності, є кільцем без дільників нуля. Отже, прийшли до протиріччя. 12. Довести, що число 4 в кільці Розв‘язок. Знайдемо дільники одиниці в ( Знайдемо норму обох частин цієї рівності
Норма числа Рівність (*) виконується, якщо Отже, в кільці Доведемо, що для числа 4 в кільці Покажемо, що 2, Число 4 розкладається в добуток натуральних чисел двома способами: 4=2×2 =1×4. Якщо Якщо Якщо 13. Довести, якщо поле Р має характеристику р, то р – просте число. Розв‘язок. Нехай р – число складене і p = st, де s < p, t < p. Тоді одержуємо
тобто (se)×(te) = 0. Оскільки в полі не існує дільників нуля, то із рівності (se)×(te) = 0 випливає, що або se = 0, або te = 0, а це суперечить умові, що поле Р має характеристику р. отже, припущення, що р – складене число, невірне. Контрольна робота № 2
І. Знайти найбільший спільний дільник многочленів f(x) і g(x) та підібрати такі многочлени m(x) і n(x), що f(x)m(x) + g(x)n(x) = d(x). 1) f(x) = x 4 + x 3 – 3 x 2 – 4 x – 1; g(x) = x 3 + x 2 – x – 1; 2) f(x) = x 6 – 7 x 4 + 8 x 3 – 7 x + 7; g(x) = 3 x 5 – 7 x 3 + 3 x 2 – 7; 3) f(x) = x 5 + x 4 – x 3 – 3 x 2 – 3 x – 1; g(x) = x 4 – 2 x 3 – x 2 – 2 x + 1; 4) f(x) = x 4 – 10 x 2 +1; g(x) = x 4 – 4 5) f(x) = x 5 + 3 x 4 + x 3 + x 2 + 3 x + 1; g(x) = x 4 + 2 x 3 + x + 2; 6) f(x) = 4 x 4 – 2 x 3 – 16 x 2 + 5 x + 9; g(x) = 2 x 3 – x 2 – 4 x + 4; 7) f(x) = x 4 – x 3 – 4 x 2 + 4 x + 1; g(x) = x 2 – x – 1; 8) f(x) = x 5 – 5 x 4 – 2 x 3 + 12 x 2 – 2 x + 12; g(x) = x 3 – 5 x 2 – 3 x + 17; 9) f(x) = 3 x 4 – 3 x 3 + 4 x 2 – x + 1; g(x) = 2 x 3 – x 2 + x + 1; 10) f(x) = x 4 + x 3 + x 2 + x + 1; g(x) = 4 x 3 + 3 x 2 + 2 x + 1. ІІ. Користуючись схемою Горнера: а) розкласти многочлен f(x) за степенями (х – а) і одержаний розклад розташувати за спадними степенями х; б) знайти канонічний розклад (відокремити кратні множники); в) знайти значення многочлена f(x) та його похідних при х = а. 1) f(x) = x 4 + 3 x 3 – 8 x 2 + 4 x – 1; a = 2; 2) f(x) = x 5 + 3 x 4 – 9 x 3 – 7 x 2 + 39 x – 21; a = 1; 3) f(x) = x 4 – 2 x 3 – 5 x 2 + 2 x + 2; a = –2; 4) f(x) = x 6 – 6 x 4 – 4 x 3 + 9 x 2 + 12 x + 2; a = 3; 5) f(x) = x 5 – 10 x 3 – 20 x 2 – 15 x – 4; a = –1; 6) f(x) = x 5 – 6 x 4 + 16 x 3 – 24 x 2 + 20 x – 8; a = –3; 7) f(x) = x 6 – 2 x 5 – x 4 – 2 x 3 + 5 x 2 + 4 x + 4; a = 1; 8) f(x) = x 6 – 15 x 4 + 8 x 3 + 51 x 2 – 72 x + 27; a = –1; 9) f(x) = x 7 – 3 x 6 + 5 x 5 – 7 x 4 + 7 x 3 – 5 x 2 + 3 x – 1; a = 2; 10) f(x) = 3 x 4 + 6 x 3 – 2 x 2 + 1; a = –1. ІІІ. Знайти раціональні корені многочлена. 1) f(x) = x 4 – 2 x 3 – 8 x 2 + 13 x – 24; 2) f(x) = 6 x 4 + 19 x 3 – 7 x 2 – 26 x + 12; 3) f(x) = x 5 – 2 x 4 – 4 x 3 + 4 x 2 – 5 x + 6; 4) f(x) = 10 x 4 – 13 x 3 + 15 x 2 – 18 x – 24; 5) f(x) = x 4 + 2 x 3 – 13 x 2 – 38 x – 24; 6) f(x) = x 4 + 4 x 3 – 2 x 2 – 12 x + 9; 7) f(x) = x 5 + x 4 – 6 x 3 – 14 x 2 – 11 x – 3; 8) f(x) = 2 x 3 + 3 x 2 + 6 x – 4; 9) f(x) = 2 x 3 – 3 x 2 + 4 x – 5; 10) f(x) = x 4 – x 3 – 22 x 2 + 16 x + 96. ІV. Виразити через елементарні симетричні многочлени такі многочлени: 1) f (x 1, x 2, x 3) = x 13 + x 23 + x 33 – x 1 – x 2 – x 3; 2) f (x 1, x 2, x 3) = x 15 x 2 x 3 + x 25 x 1 x 3 + x 35 x 1 x 2 + 2 x 1 x 2 x 3; 3) f (x 1, x 2, x 3) = x 14 x 22 + x 24 x 12 + x 34 x 22 + x 34 x 12 + x 14 x 32 + x 24 x 32; 4) f (x 1, x 2, x 3) = x 12 x 2 + x 1 x 22 + x 12 x 3 + x 1 x 32 + x 22 x 3 + x 2 x 32; 5) f (x 1, x 2, x 3) = x 14 + x 24 + x 34 x 13 –2 x 12 x 22 – 2 x 22 x 32 – 2 x 12 x 32; 6) f (x 1, x 2, x 3) = (x 1 – x 2)2 + (x 1 – x 3)2 + (x 2 – x 3)2; 7) f (x 1, x 2, x 3) = (x 1 + x 2 – 5 x 3) (x 2 + x 3 – 5 x 1) (x 1 + x 3 – 5 x 2); 8) f (x 1, x 2, x 3) = 3 x 13 – 3 x 23 + 3 x 33 + x 1 + x 2 + x 3; 9) f (x 1, x 2, x 3) = 3 x 13 + 3 x 23 + 3 x 33 + 5 x 1 x 2 x 3 + 2 x 12 + 2 x 22 + 2 x 32; 10) f (x 1, x 2, x 3) = (x 1 – x 2)(x 2 – x 3)(x 3 – x 1). V. У множині дійсних чисел розв’язати такі системи рівнянь: 1) 4) 6) 8) 10) VI. Позбавити від алгебраїчної ірраціональності в знаменнику дробу: 1) 4)
6) 9) VІІ. Довести, що число a є алгебраїчним над полем Q і знайти його мінімальний многочлен, якщо:
VІІІ. Розкласти на незвідні у полі Q множники такі многочлени: 1) f(x) = x 4 + x 3 – 6 x 2 – 7 x – 7; 2) f(x) = x 4 – x 3 – 6 x 2 + 8 x – 2; 3) f(x) = 6 x 4 – 13 x 3 + 12 x 2 – 13 x + 6; 4) f(x) = 9 x 4 – 15 x 3 + 28 x 2 – 20 x + 16; 5) f(x) = (x + 3)4 + (x + 5)4 – 16; 6) f(x) = (x + 1)6 – 9(x + 1)3 + 20; 7) f(x) = x 4 + 4 x 3 + 4 x 2 + 1; 8) f(x) = x 3 – 6 x 2 + 11 x – 6; 9) f(x) = x 4 + 3 x 3 – 3 x 2 – 11 x – 6; 10) f(x) = x 5 – x 3 – x 2 + 1.
Зразок розв‘язання контрольної роботи № 2 Варіант 0.
1. Знайти найбільший спільний дільник многочленів f(x) і g(x) та підібрати такі многочлени m(x) і n(x), що f(x)m(x) + g(x)n(x) = d(x). f(x) = 2 x 4 + 3 x 3 – 3 x 2 – 5 x + 2; g(x) = 2 x 3 + x 2 – x – 1. Розв‘язок. До многочленів f(x) і g(x) застосовуємо алгоритм Евкліда:
Отже, в результаті ділення одержуємо: f(x) = g(x)q 1 (x) + r 1 (x); q 1 (x) = x + 1, r 1 (x) = – 3 x 2 – 3 x + 3; g(x) = r 1 (x)q 2 (x) + r 2 (x); q 2 (x) = r 1 (x) = r 2 (x)q 3 (x) + r 3 (x); q 3 (x) = Так як r 3 (x) = – 3 є стале число, а на стале число без остачі ділиться будь-який многочлен, то наступна остача r 4 (x) буде дорівнювати нулю. Отже, алгоритм Евкліда записався тут у три рядки, а найбільший спільний дільник дорівнює – 3, або d(x) = 1 = – Щоб виразити d(x) через многочлени m(x) і n(x) виразимо спочатку через них r 3 (x). r 3 (x) = r 1 (x) – r 2 (x) q 3 (x), r 3 (x) = r 1 (x) – [ g(x) – r 1 (x)q 2 (x) ] q 3 (x), або r 3 (x) = r 1 (x) [1 + q 2 (x)q 3 (x) ] – g(x)q 3 (x). В останню рівність замість r 1 (x) підставимо його вираз з першого рядка алгоритму Евкліда, одержимо: r 3 (x) = [ f(x) – g(x)q 1 (x) ]×[1 + q 2 (x)q 3 (x) ] – g(x)q 3 (x) = = –f(x) [1 + q 2 (x)q 3 (x) ] + g(x) [ –q 1 (x) – q 1 (x)q 2 (x)q 3 (x) – q 3 (x) ]. Враховуючи, що d(x) = –
Отже,
де q 1 (x) = x + 1; q 2 (x) = Одержуємо: Відповідь: ІІ. Користуючись схемою Горнера: а) розкласти многочлен f(x) за степенями (х – а) і одержаний розклад розташувати за спадними степенями х; б) знайти канонічний розклад (відокремити кратні множники); в) знайти значення многочлена f(x) та його похідних при х = а, якщо f(x) = x 6 – 6 x 4 – 4 x 3 + 9 x 2 + 12 x + 4, a = –2. Розв‘язок.
а) За схемою Горнера маємо:
Звідси f(x) = (x + 2)6 – 12(x + 2)5 + 54(x + 2)4 – 116(x + 2)3 + + 129(x + 2)2 – 72(x + 2) + 16 = F (x + 2). Розташуємо многочлен F (x + 2) за степенями х. запишемо х у вигляді x = (x + 2) – 2 і за схемою Горнера розділимо F (x + 2) на двочлен (x + 2) – 2, одержуємо:
Отже, F (x + 2) = x 6 – 6 x 4 – 4 x 3 + 9 x 2 + 12 x + 4. б) Знайдемо d 1 = (f, f¢), де f¢ = 6 x 5 – 24 x 3 – 12 x 2 + 18 x + 12. Застосовуючи алгоритм Евкліда для многочленів f і f¢, одержуємо: d 1 = x 4 + x 3 – 3 x 2 – 5 x – 2, d 1¢ = 4 x 3 + 3 x 2 – 6 x – 5. Знаходимо d 2 = (d 1, d 1¢); d 2 = x 2 + 2 x + 1; d 2¢ = 2 x + 2; d 3 = (d 2, d 2¢); d 3 = x + 1; d 3¢ = 1; d 4 = (d 4, d 4¢); d 4 = 1. Отже, маємо:
Тому
Враховуючи, що індекс F означає кратність, маємо: f(x) = (x – 2)2 × (x + 1)4 – канонічний розклад многочлена f(x). в) Для многочлена f(x) запишемо формулу Тейлора:
Порівняємо формулу з розкладом за степенями (х + 2). Одержуємо: f (–2) = 16; f ¢(–2) = – 72; f ¢¢(–2) = 2!×129; f ¢¢¢(–2) = –3!×116; f (IV) (–2) = 4!×54; f (V) (–2) = –5!×12; f (VI) (–2) = 6!.
ІІІ. Знайти раціональні корені многочлена f(x) = 12 x 6 + 64 x 5 + 123 x 4 + 113 x 3 + 65 x 2 + 24 x + 4. Розв‘язок. Старший коефіцієнт a 0 = 12 ¹ 1. Тому многочлен, якщо має раціональні корені, то вони можуть бути як цілими, так і дробовими. Шукаємо їх серед чисел:
Для скорочення обчислень знайдемо межі коренів многочлена f(x). Так як коефіцієнти многочлена f(x) додатні, то він не має додатних коренів і тому верхня межа дорівнює нулеві. Знайдемо нижню межу многочлена f(x) методом Ньютона. f(x) = 12 x 6 + 64 x 5 + 123 x 4 + 113 x 3 + 65 x 2 + 24 x + 4. Для f(–x) знаходимо методом Ньютона верхню межу: ВМ = –3, отже, НМ = – 3 – нижня межа для многочлена f(x). Отже, усі корені многочлена f(x) знаходяться на проміжку (–3; 0). Тому залишилися для випробувань числа:
Знаходимо цілі корені, ними можуть бути числа –1, –2. обчислюємо f (1) = 405, f (–1) = 3. так як f (–1) ¹ 0, то число –1 не є коренем f(x). Для числа –2 застосовуємо “сито”. Результат запишемо у таблицю:
Отже, число –2 підозріле на корінь.
За схемою Горнера перевіряємо, чи буде –2 коренем многочлена та визначимо його кратність:
З таблиці видно, що a = –2 є двократним коренем многочлена f(x). Знаходимо дробові корені. До чисел, що залишилися для перевірки, застосовуємо “сито”. Результати заносимо до таблиці:
Числа
Звідси маємо: a = f(x) = (x + 2 ) 2 × (x + де j(x) = 12 x 2 + 4 x + 4. Перевіряємо число a =
Отже, a = | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

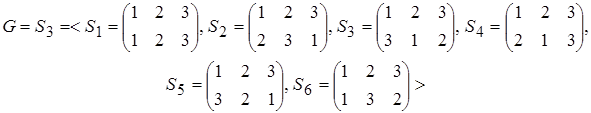
 .
. , а тому
, а тому 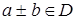 .
.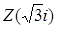 неоднозначно розкладається в добуток простих множників.
неоднозначно розкладається в добуток простих множників. ,
,  – дільники одиниці, a, b, c, d Î Z. Тоді
– дільники одиниці, a, b, c, d Î Z. Тоді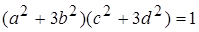 . (*)
. (*)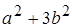 .
.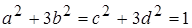 . (**) Рівність (**), в свою чергу, виконується при
. (**) Рівність (**), в свою чергу, виконується при 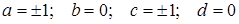 .
.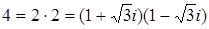 .
.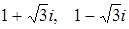 є прості числа в
є прості числа в 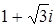 та 2,
та 2, 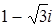 не є асоційованими. Оскільки в кільці
не є асоційованими. Оскільки в кільці  , то знайшовши норми від обох частин, дістанемо
, то знайшовши норми від обох частин, дістанемо 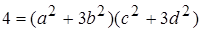 .
. , то b 2 < 1, тобто b =0. Тоді a 2 = 2, що неможливо для цілого числа a. Отже,
, то b 2 < 1, тобто b =0. Тоді a 2 = 2, що неможливо для цілого числа a. Отже,  .
.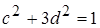 і
і 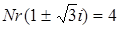 , то аналогічно доводять, що числа
, то аналогічно доводять, що числа  є простими. Отже, число 4 в кільці
є простими. Отже, число 4 в кільці 
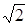 x 3 + 6 x 2 + 4
x 3 + 6 x 2 + 4 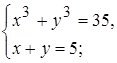 2)
2) 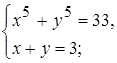 3)
3) 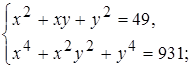
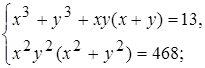 5)
5) 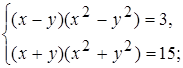
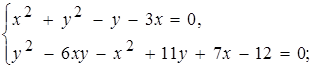 7)
7) 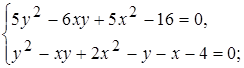
 9)
9) 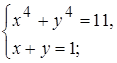
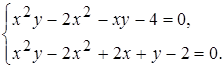
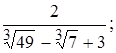 2)
2)  3)
3) 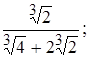
 5)
5) 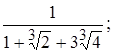
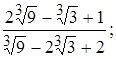 7)
7) 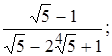 8)
8) 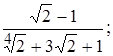
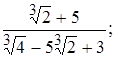 10)
10) 
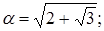
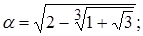



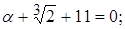

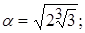

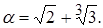
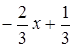
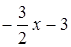
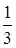 r 3 (x).
r 3 (x).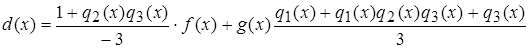 .
.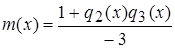 ;
;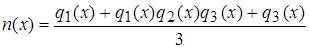 ,
,
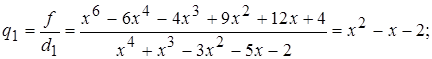


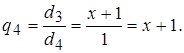

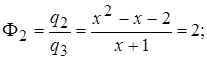
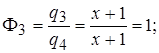
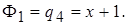
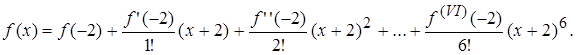
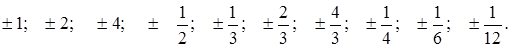

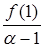


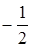
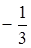

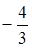
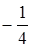

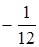
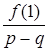
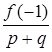
 )2 × j(x),
)2 × j(x),



