
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Властивості головних ідеалів.Содержание книги Поиск на нашем сайте
1. Будь-який елемент a 2. Головний ідеал породжений нульовим елементом 0, складається лише з цього елемента, а головний ідеал, породжений, одиничним елементом е, співпадає з самим кільцем K: (0)= <0>; (e) = K. 3. Якщо елементи b і c кільця K належать головному ідеалу (а), то і b– c 4. Якщо елемент b належить головному ідеалу (а), то всі елементи вигляду rb, r 5. Елемент a a 6. Асоційовані елементи кільця K породжують один і той же головний ідеал. 7. Головний ідеал породжений зворотнім елементом 8. Якщо головні ідеали, породжені елементами a і b області цілісності K, співпадають (а) = (b), то елементи a і b асоційовані в K. Означення 3. Підмножина I кільця K називається ідеалом в K, якщо: 1. З будь-якими двома елементами a і b підмножина I містить їх різницю: a 2. Разом з кожним елементом а підмножина I містить кратні цього елемента: a Кожний головний ідеал кільця K є ідеалом цього кільця. Будь-який ідеал кільця K є підкільцем в K. Означення 4. Ідеал I, що складається із елементів вигляду r1a1+r2a2+…+rnan, де ai – деякі елементи з підмножини A Теорема 1. Перетин I1 Теорема 2. Перетин будь-якої множини ідеалів кільця K є ідеалом в кільці K. Найменшим ідеалом, що містить множену А, є перетин усіх ідеалів, що містять цю множину. Теорема 3. Найменший ідеал I(А) кільця K, що містить підмножину А цього кільця, співпадає з ідеалом (А), породженим підмножиною А. Означення 5. Ідеал I1 кільця K ділиться на ідеал I 2 того ж кільця, якщо I1 Означення 6. Ідеал I кільця K називається найбільшим спільним дільником ідеалів I 1 і I 2 цього кільця, якщо 1. I є дільником I 1 і I 2; 2. I ділиться на будь-який спільний дільник I 1 і I 2. Теорема 4. Будь-які два ідеали I 1 і I 2 кільця K мають найбільший спільний дільник. Ним є ідеал, породжений множиною I1 Означення 7. Елементи a і b кільця K конгруентні за ідеалом I, якщо Відношення конгруентності елементів із множини деякого кільця K за його ідеалом I є бінарним відношенням еквівалентності.
Класи еквівалентності називають ще класами лишків кільця K за ідеалом I або суміжними класами групи K за підгрупою I. Множину всіх класів лишків кільця K за його ідеалом I позначають У множині алгебраїчними є операції додавання і множення класів лишків: Множина Якщо K = Z, а I – ідеал кільця Z, то I – головний ідеал, породжений деяким числом m, m Контрольні запитання для самоперевірки. 1. Дайте означення підкільця. 2. Що таке головний ідеал? Який головний ідеал в кільці Z породжується числом 7? 3. У якому випадку елементи а і b кільця K породжують один і той же головний ідеал? 4. У якому випадку головний ідеал, породжений елементом а, співпадає з усім кільцем K? Який головний ідеал породжує елемент 2– 5. Як вибрати на “мові ідеалів” твердження: елемент а ділиться на елемент b? 6. Чи є будь-яке підкільце ідеалом? Якій додатковій умові воно повинно задовольняти? 7. Чи є ідеалом в Z [ x ] підкільце, що складається з многочленів, вільний член якого ділиться на 3? 8. Чи є підкільцем в Z [ x ] множина многочленів з додатнім вільним членом? 9. В кільці Z [ 10. Що означає твердження “ідеал I 1 ділиться на ідеал I 2”? 11. Знайдіть ідеал в кільці Z [ x ] многочленів з цілими коефіцієнтами, породжений елементами x 2 і 4. 12. Який ідеал називається найбільшим спільним дільником ідеалів I 1 і I 2? Які його властивості? 13. Які відомі вам кільця є кільцями головних ідеалів? 14. Напишіть таблиці додавання і множення 15. В кільці Z [ x ] многочленів з цілими коефіцієнтами знайдіть ідеал (x 2+1) і побудуйте фактор-кільце 16. В кільці Z [ i ] цілих гаусових чисел побудуйте ідеал (i) і фактор-кільце Література: [4], гл. III 13; [2], гл. 4, 4 (3). [3], гл. 13, 1. Лекція 7.
|
|||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 360; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.158.197 (0.006 с.) |

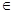 K належить породженому ним головному ідеалу: a
K належить породженому ним головному ідеалу: a  (b):
(b):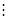 b
b  (a)
(a) 
 K, співпадає з K, (
K, співпадає з K, ( b
b  a–b
a–b  I2 двох ідеалів I1 і I2 кільця K є ідеалом цього ж кільця.
I2 двох ідеалів I1 і I2 кільця K є ідеалом цього ж кільця. I2, тобто найменший ідеал, що містить ідеали I 1 і I 2.
I2, тобто найменший ідеал, що містить ідеали I 1 і I 2. b (mod I).
b (mod I). =
=  .
. ;
;  .
. позначають Zm.
позначають Zm. в кільці Z [
в кільці Z [  ] елемент 2+
] елемент 2+  і
і  .
. ізоморфне кільцю Z [i] цілих гаусових чисел.
ізоморфне кільцю Z [i] цілих гаусових чисел. .
.


