
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема: Гомоморфізми кілець. Евклідові кільця.Содержание книги Поиск на нашем сайте
План. 1. Гомоморфізми кілець, означення, приклади. 2. Ядро гомоморфізму. 3. Теорема про гомоморфізми. 4. Кільце головних ідеалів. 5. Евклідові кільця. Короткий зміст лекції: Означення 1. Відображення 1. 2. Взаємно однозначний гомоморфізм називається ізоморфізмом. Теорема 1. Якщо 1. 2. 3. 4. Якщо K – кільце з одиницею е, то Означення 2. Множина усіх елементів кільця K, які відображаються в 0’ кільця K ', називається ядром гомоморфізму Теорема 2. Ядро Теорема про гомоморфізм кілець. Якщо
Отже, всі кільця, що гомоморфні до кільця K, ізоморфні фактор-кільцям цього кільця. Означення 3.Кільцем головних ідеалів називається область цілісності з одиницею, в якій кожний ідеал є головним. Теорема 3. Нехай R – кільце головних ідеалів і будь-які два елемента a і b кільця головних ідеалів мають найбільший спільний дільник d, причому d = ra+sb, де r і s – деякі елементи кільця R. Теорема 4. Елементи a і b кільця головних ідеалів R взаємно прості тоді і тільки тоді, коли в кільці R є такі елементи r і s, що ra+sb = 1. Теорема 5. Якщо елемент а взаємно простий з кожним із елементів b і c, то він взаємно простий і з добутком bc цих елементів. Теорема 6. В кільці головних ідеалів R кожний відмінний від нуля елемент, що не є дільником одиниці, розкладається в добуток простих множників. Означення 4. Кільце K називається факторіальним, якщо воно є областю цілісності і будь-який відмінний від нуля незворотній елемент кільця однозначно розкладається на прості множники. Кільце головних ідеалів факторіальне. Означення 5. Область цілісності R з одиницею називається евклідовим кільцем, якщо існує відображення Теорема 7. Кожне евклідове кільце R є кільцем головних ідеалів. Отже, евклідове кільце факторіальне. Кільце цілих чисел Z є кільцем головних ідеалів, отже, воно факторіальне. Контрольні питання для самоперевірки. 1. Дайте означення гомоморфізму кілець Які кільця називають ізоморфними? 2. Нехай R кільце із елементів a,b,c з правилами дій, вказаних в таблицях:
Поставимо у відповідність цілому числу х елемент а, якщо х ділиться на 3, елемент b, якщо остача від ділення х на 3 дорівнює 1, і елемент с, якщо остача дорівнює 2. Покажіть, що це відображення є гомоморфним відображенням Z на R. 3. Що називається ядром гомоморфізму? Чи можна бути будь-яка підмножина кільця ядром гомоморфізму? 4. Чи може бути будь-який ідеал ядром гомоморфізму? В кожному класі лишків за ідеалом (х 2) в кільці Z [ x ] є многочлен першого степеня a+bx. Як визначити додавання та множення таких многочленів, щоб одержалося кільце, ізоморфне фактор-кільцю 5. Дайте означення кільця головних ідеалів, евклідового кільця. 6. Доведіть що кільце Z [ Література: [4], гл. III, 13,14; [2] гл. 4, 4(3); [3] гл. 13, 1. Лекція 8. Тема: Поле. План. 1. Означення поля, приклади полів. 2. Властивості полів. 3. Характеристика поля. 4. Підполе. 5. Поле часток. Короткий зміст лекції. Означення 1. Комутативне кільце Р називається полем, якщо в ньому є як найменше один елемент, відмінний від нуля і виконується операція ділення, крім ділення на нуль, тобто для Властивості полів: 1. В кожному полі Р існує, і при тому тільки одна одиниця. 2. В кожному полі Р для будь-якого елемента а, відмінного від нуля, існує, і при тому тільки один обернений елемент а -1. 3. Будь-яке поле Р не має дільників нуля. 4. В кожному полір множина відмінних від нуля елементів Р * є абелевою групою відносно множення (мультиплікативна група поля Р). Означення 2.Характеристикою поля Р називають число нуль, якщо ne = 0 тільки при n = 0; характеристикою поля Р називають натуральне число р, якщо ре = 0; немає такого натурального числа к, менше р, що ке = 0. Усі числові поля мають характеристику нуль. Теорема 1. Якщо поле Р має характеристику р, то число р – просте. Теорема 2. Якщо Р – поле характеристики нуль, то будь-яке ціле кратне будь-якого відмінного від нуля елемента а цього поля не дорівнює нулю: na Означення 3. Підмножина Р ’ поля Р називається підполем цього поля, якщо вона сама є полем відносно алгебраїчних операцій, визначених в полі Р. Поле Р в цьому випадку називається розширенням поля Р ’. Критерій поля: Для того щоб підмножина Р ’ поля Р, в якій є хоч би один відмінний від нуля елемент, була підполем, необхідно і достатньо, щоб сума, різниця, добуток і частка (якщо вона існує) будь-яких двох елементів підмножини Р містилась в підмножині Р ’. Означення 4. Підполе, що складається із нуля і одиниці поля Р, називається тривіальним підполем поля Р. Означення 5. Підполе, відмінне від тривіального, називається власним підполем. Означення 6. Поле називається простим, якщо в ньому немає власних підполів. Теорема 3. Перетин будь-якої множини підполів поля Р є підполем в полі Р. Теорема 4. Будь-яке підполе Р ’ поля Р, що містить ненульове підкільце R, містить усі дроби Теорема 5. Нехай R – ненульове підкільце поля Р. Підмножина S в P, що складається із елементів вигляду Теорема 6. Якщо R – підкільце поля Р, то найменше поле в Р, що містить R, складається із дробів Теорема 7. Будь-яка область цілісності R з одиницею є підкільцем деякого поля Р. Найменше підполе Р, що містить кільце R, співпадає з Р. Тому Р називають полем відношень кільця R. Теорема 8. Якщо R – кільце головних ідеалів і р – простий елемент цього кільця, то фактор-кільце Будь-яке поле містить просте підполе, ізоморфне або полю раціональних чисел Q, або полю лишків Zp кільця цілих чисел за модулем р, р – просте число. Число елементів скінченого поля Р дорівнює рn, де р – характеристика поля, а n – розмірність поля Р як векторного простору над його простим підполем. При заданих числах p і n усі поля з рn елементів ізоморфні. Контрольні запитання для самоперевірки. 1. Дайте означення поля. 2. Доведіть найпростіші властивості поля. 3. Дайте означення характеристики поля. 4. Доведіть, що характеристикою будь-якого поля є нуль або просте число. 5. Доведіть, що найменше підполе будь-якого поля характеристики нуль ізоморфне полю раціональних чисел. 6. Що таке поле відношень? Які кільця мають поле відношень? 7. Яке поле називають простим? 8. Довести, що в полі немає ідеалів, відмінних від нульового і одиничного. 9. Довести, що при будь-якому ізоморфізмі числових полів, підполе раціональних чисел відображається тотожньо. 10. Довести, що будь-яка скінченна область цілісності є полем. Література: [2], гл. 4, 4(5,6); [1], гл. 10, 45.
Лекція 9.
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 595; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.134.195 (0.01 с.) |

 кільця K в кільце K' називається гомоморфізмом K в K’, якщо виконуються наступні умови:
кільця K в кільце K' називається гомоморфізмом K в K’, якщо виконуються наступні умови: a,b
a,b 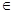 K [
K [ 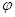 (a+b) =
(a+b) = 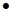
 .
. , причому існує такий гомоморфізм
, причому існує такий гомоморфізм  кільця
кільця  природного гомоморфізму
природного гомоморфізму  на ізоморфізм
на ізоморфізм  Замкнена діаграма цих відображень має наступний вигляд:
Замкнена діаграма цих відображень має наступний вигляд: , яке задовольняє умові:
, яке задовольняє умові: 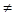 0 в R існують такі елементи q і r, що a = bq+r, причому або r = 0, або
0 в R існують такі елементи q і r, що a = bq+r, причому або r = 0, або 
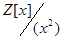 ?
? ] з нормою Nr (a+b
] з нормою Nr (a+b  .
. , де a
, де a  ).
). рівні тоді і тільки тоді, коли ad = cb.
рівні тоді і тільки тоді, коли ad = cb. є поле.
є поле.


