
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Диференціальні системи екстремального керуванняСодержание книги
Поиск на нашем сайте
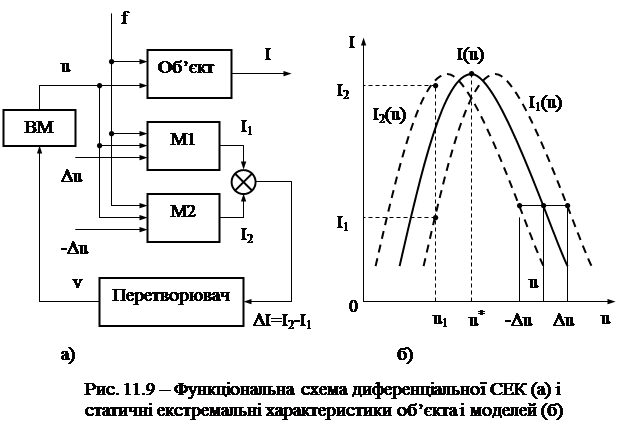
Дані системи працюють за розімкнутим циклом, і тому іноді їх називають безпошуковими. Керуюча дія у таких системах формується за допомогою аналізу різниці двох величин. Це й обумовило їх назву. Функціональна схема диференціальної СЕК наведена на рис. 11.9, а). Керуюча дія u і збурення f прикладені не тільки до об’єкта керування, але й до двох його моделей М. Крім того, на ці моделі діють однакові й постійні за модулем, але різні за знаком додаткові керуючі дії D u, у результаті чого статичні екстремальні характеристики моделей I1(u) і I2(u) зміщуються у різні боки відносно характеристики об’єкта I(u) (рис. 11.9, б). Нехай на вхід обох моделей і об’єкта подається керування u1. Тоді вихідна величина першої моделі дорівнює І1, другої – І2, а різниця DІ=І2 -І1>0. Можна показати, що у разі параболічної залежності І(u) різниця DІ буде пропорційною відстані до екстремальної точки u*. У точці екстремуму u* ця різниця дорівнює нулю, а надалі при переході на праву частину характеристики вона змінює свій знак. Таким чином, формуючи змінювання керуючої дії u пропорційно різниці DІ (або відповідно до його знаку), можна забезпечити роботу системи в екстремальній точці. Оскільки на модель діють ті самі збурення, що і на об’єкт, дрейф характеристики об’єкта не змінює відносного розташування вихідних характеристик моделей і характеристики об’єкта, і не порушує працездатності системи.
Суттєвим обмежуючим моментом застосування диференціальних СЕК є необхідність апріорного знання моделі об’єкта, яка невідома для широкого класу об’єктів. У разі, якщо функція I(u) має мінімум, то шляхом віднімання її від постійної величини А отримаємо криву, яка має максимум. Завдяки цьому екстремальний регулятор, призначений для пошуку максимуму функції I1(u), можна використовувати і для пошуку мінімуму функції I(u) = А - I1(u).
Розглянуті методи пошуку екстремуму стосуються одноканальних систем. Якщо показник екстремуму є функцією кількох керуючих параметрів І(u1, u2, …, um) (багатоканальні системи), то необхідною умовою досягнення екстремуму є рівність нулю частинних похідних показника якості зі всіх керуючих параметрів:
Методи пошуку екстремуму для таких систем поділяються на два види: - детерміновані: метод градієнта, метод найшвидшого спуску, метод Гаусса-Зейделя; - випадкові: метод випадкових сліпих пошуків, статистичного градієнта та статистичного найшвидшого спуску. Метод градієнта Градієнтом скалярної функції І(u1, u2, …, um) називається вектор з координатами
де k 1, k 2, …, k m – одиничні вектори, напрямки яких збігаються з напрямками осей u1, u2, …, um. Цей вектор спрямований у бік найбільшого зростання функції І. У точці екстремуму grad I = 0. Метод градієнта реалізується на основі дискретного або безперервного принципу роботи контуру адаптації. При безперервному принципі роботи метод градієнта полягає у тому, що швидкості змінювання параметрів ui беруть пропорційними відповідним компонентам миттєвого значення градієнта, тобто
де сі – коефіцієнт пропорційності; сі > 0 для випадку екстремуму-мінімуму; сі<0 для екстремуму-максимуму. При кроковому пошуку після вимірювання поточного градієнта виконується крок, складові якого за осями координат пропорційні відповідним компонентам градієнта у початковій точці пошуку:
Далі знову визначається градієнт, виконується наступний крок у напрямку вектора градієнта і т.д. Залежності (11.4) і (11.5) використовують для формування робочих сигналів екстремальної системи, що забезпечують рух до екстремуму вихідної величини І. Перевагою методу градієнта є плавний характер руху до точки екстремуму і у разі крокового пошуку відносно малий розмах коливань. До недоліків належить необхідність визначення градієнта в кожній точці фазової траєкторії, що збільшує час пошуку.
Метод найшвидшого спуску За цим методом напрямок градієнта визначається у початковій точці, а потім здійснюється рух у цьому напрямку доти, доки похідна вздовж цього напрямку dI/dt не дорівнюватиме нулю. Потім знову визначається напрямок градієнта і здійснюється рух за новим напрямком до наступного нульового значення похідної і т.д. Метод найшвидшого спуску характеризується відносно малим часом досягнення екстремуму при великих кроках на початковому етапі пошуків. Приклад 11.1 Задано показник екстремуму:
Визначити мінімум функції I(u1, u2) методом найшвидшого спуску з початкової точки u10 = 4; u20 = 6. Функції I(u1, u2) відповідає сім’я еліпсів для різних I = const (рис. 11.10). Початковий стан визначається точкою М1. Знайдемо напрямок градієнта у початковій точці. Частинні похідні для цієї точки:
Через те, що відшукуємо мінімум функції І, будемо рухатись у напрямку, зворотному до градієнта, і визначимо координати u11, u21 наступної точки:
де L – поки ще невідомий крок переходу з точки (u10, u20) до точки (u11, u21).
Прирівняємо до нуля похідну
звідки L = 0,334. Підставимо це значення у вираз (11.8) і визначимо координати u11 і u21: u11 = -0,68; u21 = 0,65 (точка М12 на рис. 11.10). Виконавши аналогічні обчислення для наступного кроку за умови, що вихідним станом системи є стан, у який вона прийшла у кінці першого кроку, дістанемо: u12 = 0,0229; u22 = 0,0362. Отже, практично за два кроки система опиняється у точці, досить близькій до точки мінімуму.
Метод Гаусса-Зейделя (метод почергового змінювання параметрів) За цим методом рух уздовж кожної координати відбувається по черзі. Спочатку здійснюється рух уздовж координати u1, а решта координат u2, u3, … залишаються незмінними. Цей рух триває доти, доки похідна функції І по координаті u1 не дорівнюватиме нулю, тобто Приклад 11.2 Розв’язати задачу (приклад 11.1) методом Гаусса-Зейделя. Початковий стан об’єкта визначається точкою М1 (рис. 11.10). Починаємо пошук, змінюючи координату u1 при u2 = 6. Тоді
Визначимо частинну похідну даної функції за u1 і прирівняємо її до нуля:
звідки для першого частинного екстремуму u1 = -3. Йому відповідає точка М2 з координатами u1 = -3, u2 = 6. Фіксуємо параметр u1 = -3 і змінюємо координату u2:
Цьому значенню координати u2 відповідає точка М3. Повторимо обчислення для координати u1 при u2 = 1,5:
Отримали точку М4(-0,75;1,5). Наступний цикл:
Цьому циклу відповідає точка М5. Отже, пошукові рухи становлять ламану лінію, яка складається з взаємно перпендикулярних відрізків. Точки зламу є точками дотику цих відрізків до кривих I(u1,u2)=const.
Метод змінювання параметрів зручний тим, що для його реалізації можна застосовувати відомі типи однопараметричних екстремальних систем, якщо додати пристрій, що перемикає канали параметрів u1, u2, …, um. Проте, як видно з рис. 11.10, рух системи до екстремуму відбувається далеко не найкоротшим шляхом.
|
|||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 192; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.187.60 (0.006 с.) |

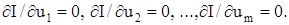 (11.2)
(11.2)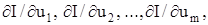 тобто
тобто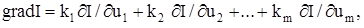 (11.3)
(11.3)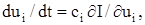 (11.4)
(11.4)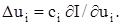 (11.5)
(11.5)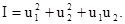 (11.6)
(11.6)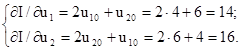 (11.7)
(11.7)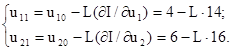 (11.8)
(11.8)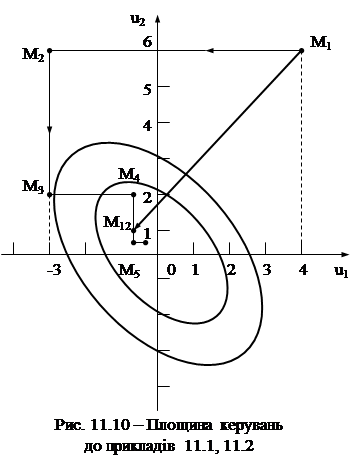 Для визначення кроку L підставимо знайдені значення u11, u21 у вираз (11.6):
Для визначення кроку L підставимо знайдені значення u11, u21 у вираз (11.6):
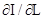 і отримаємо:
і отримаємо:
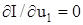 . З останньої умови визначається u1. Після цього значення u1 і решта координат, крім u2, залишаються незмінними, а координата u2 змінюється доти, доки не буде виконана умова
. З останньої умови визначається u1. Після цього значення u1 і решта координат, крім u2, залишаються незмінними, а координата u2 змінюється доти, доки не буде виконана умова  . З цієї умови визначається u2. Потім змінюється координата u3 і т.д. У такій спосіб визначаються частинні екстремуми по всіх координатах. Після цього виконується повторний цикл змінювання координат по черзі, починаючи з u1. Процес пошуку триває, доки всі частинні похідні не дорівнюватимуть нулю (доки всі похідні не будуть меншими за поріг чутливості системи).
. З цієї умови визначається u2. Потім змінюється координата u3 і т.д. У такій спосіб визначаються частинні екстремуми по всіх координатах. Після цього виконується повторний цикл змінювання координат по черзі, починаючи з u1. Процес пошуку триває, доки всі частинні похідні не дорівнюватимуть нулю (доки всі похідні не будуть меншими за поріг чутливості системи).
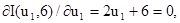

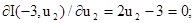 u2 = 1,5.
u2 = 1,5.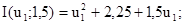
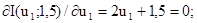 u1 = -0,75.
u1 = -0,75.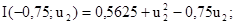
 u2 = 0,375.
u2 = 0,375.


