
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Адаптивні системи автоматичного керуванняСодержание книги
Поиск на нашем сайте АДАПТИВНІ СИСТЕМИ АВТОМАТИЧНОГО КЕРУВАННЯ
Системи екстремального керування з безпосереднім вимірюванням похідної У цих системах необхідно вимірювати похідні dI/du або dI/dt, або у крайньому разі, знак похідної dI/du. Як приклад, розглянемо дизель-генератор, що працює паралельно з енергосистемою. Необхідно забезпечити таке керування цим агрегатом, щоб його коефіцієнт корисної дії h був увесь час максимальним. У результаті випадкової зміни параметрів установки залежність h від витрати палива q, що подається до дизеля, h=f(q) нестабільна. Екстремальне значення h буде за умови dh/dq = 0. Тому для забезпечення екстремального керування дизель-генератором необхідно обчислити h, визначити його похідну по q і так здійснювати керування, щоб ця похідна весь час дорівнювала нулю. Функціональна схема СЕК для даного випадку наведена на рис. 11.3. Інформація про вхідну потужність Рвх, яка пропорційна до витрат палива q, і про потужність генератора Рг дає змогу безперервно вимірювати к.к.д установки: h = Рг / Рвх. Диференціювання величин h і q за часом з подальшим діленням похідних визначить величину dh/dq, пропорційну до керуючої дії, яка надходить на виконавчий механізм. Останній відповідно до знаку і величини похідної dh/dq змінює витрату палива. Оскільки швидкість змінювання q пропорційна величині dh/dq, то такі СЕК іноді називають системами з пропорційним керуванням. Зазначимо, що при вимірюванні похідної dh/dt замість dh/dq функціонування системи не зміниться, якщо об’єкт є безінерційним.
Метод градієнта Градієнтом скалярної функції І(u1, u2, …, um) називається вектор з координатами
де k 1, k 2, …, k m – одиничні вектори, напрямки яких збігаються з напрямками осей u1, u2, …, um. Цей вектор спрямований у бік найбільшого зростання функції І. У точці екстремуму grad I = 0. Метод градієнта реалізується на основі дискретного або безперервного принципу роботи контуру адаптації. При безперервному принципі роботи метод градієнта полягає у тому, що швидкості змінювання параметрів ui беруть пропорційними відповідним компонентам миттєвого значення градієнта, тобто
де сі – коефіцієнт пропорційності; сі > 0 для випадку екстремуму-мінімуму; сі<0 для екстремуму-максимуму. При кроковому пошуку після вимірювання поточного градієнта виконується крок, складові якого за осями координат пропорційні відповідним компонентам градієнта у початковій точці пошуку:
Далі знову визначається градієнт, виконується наступний крок у напрямку вектора градієнта і т.д. Залежності (11.4) і (11.5) використовують для формування робочих сигналів екстремальної системи, що забезпечують рух до екстремуму вихідної величини І. Перевагою методу градієнта є плавний характер руху до точки екстремуму і у разі крокового пошуку відносно малий розмах коливань. До недоліків належить необхідність визначення градієнта в кожній точці фазової траєкторії, що збільшує час пошуку.
Метод найшвидшого спуску За цим методом напрямок градієнта визначається у початковій точці, а потім здійснюється рух у цьому напрямку доти, доки похідна вздовж цього напрямку dI/dt не дорівнюватиме нулю. Потім знову визначається напрямок градієнта і здійснюється рух за новим напрямком до наступного нульового значення похідної і т.д. Метод найшвидшого спуску характеризується відносно малим часом досягнення екстремуму при великих кроках на початковому етапі пошуків. Приклад 11.1 Задано показник екстремуму:
Визначити мінімум функції I(u1, u2) методом найшвидшого спуску з початкової точки u10 = 4; u20 = 6. Функції I(u1, u2) відповідає сім’я еліпсів для різних I = const (рис. 11.10). Початковий стан визначається точкою М1. Знайдемо напрямок градієнта у початковій точці. Частинні похідні для цієї точки:
Через те, що відшукуємо мінімум функції І, будемо рухатись у напрямку, зворотному до градієнта, і визначимо координати u11, u21 наступної точки:
де L – поки ще невідомий крок переходу з точки (u10, u20) до точки (u11, u21).
Прирівняємо до нуля похідну
звідки L = 0,334. Підставимо це значення у вираз (11.8) і визначимо координати u11 і u21: u11 = -0,68; u21 = 0,65 (точка М12 на рис. 11.10). Виконавши аналогічні обчислення для наступного кроку за умови, що вихідним станом системи є стан, у який вона прийшла у кінці першого кроку, дістанемо: u12 = 0,0229; u22 = 0,0362. Отже, практично за два кроки система опиняється у точці, досить близькій до точки мінімуму.
Метод Гаусса-Зейделя (метод почергового змінювання параметрів) За цим методом рух уздовж кожної координати відбувається по черзі. Спочатку здійснюється рух уздовж координати u1, а решта координат u2, u3, … залишаються незмінними. Цей рух триває доти, доки похідна функції І по координаті u1 не дорівнюватиме нулю, тобто Приклад 11.2 Розв’язати задачу (приклад 11.1) методом Гаусса-Зейделя. Початковий стан об’єкта визначається точкою М1 (рис. 11.10). Починаємо пошук, змінюючи координату u1 при u2 = 6. Тоді
Визначимо частинну похідну даної функції за u1 і прирівняємо її до нуля:
звідки для першого частинного екстремуму u1 = -3. Йому відповідає точка М2 з координатами u1 = -3, u2 = 6. Фіксуємо параметр u1 = -3 і змінюємо координату u2:
Цьому значенню координати u2 відповідає точка М3. Повторимо обчислення для координати u1 при u2 = 1,5:
Отримали точку М4(-0,75;1,5). Наступний цикл:
Цьому циклу відповідає точка М5. Отже, пошукові рухи становлять ламану лінію, яка складається з взаємно перпендикулярних відрізків. Точки зламу є точками дотику цих відрізків до кривих I(u1,u2)=const.
Метод змінювання параметрів зручний тим, що для його реалізації можна застосовувати відомі типи однопараметричних екстремальних систем, якщо додати пристрій, що перемикає канали параметрів u1, u2, …, um. Проте, як видно з рис. 11.10, рух системи до екстремуму відбувається далеко не найкоротшим шляхом. АДАПТИВНІ СИСТЕМИ АВТОМАТИЧНОГО КЕРУВАННЯ
|
|||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 318; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.006 с.) |


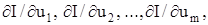 тобто
тобто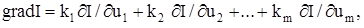 (11.3)
(11.3)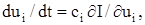 (11.4)
(11.4)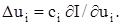 (11.5)
(11.5)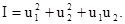 (11.6)
(11.6)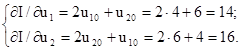 (11.7)
(11.7)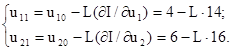 (11.8)
(11.8)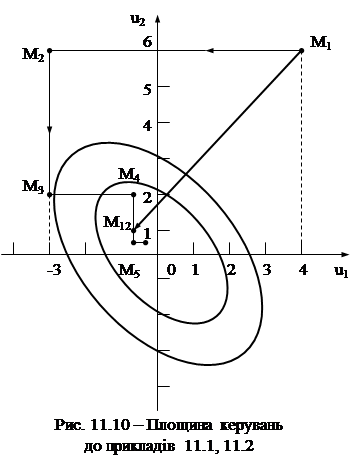 Для визначення кроку L підставимо знайдені значення u11, u21 у вираз (11.6):
Для визначення кроку L підставимо знайдені значення u11, u21 у вираз (11.6):
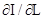 і отримаємо:
і отримаємо:
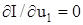 . З останньої умови визначається u1. Після цього значення u1 і решта координат, крім u2, залишаються незмінними, а координата u2 змінюється доти, доки не буде виконана умова
. З останньої умови визначається u1. Після цього значення u1 і решта координат, крім u2, залишаються незмінними, а координата u2 змінюється доти, доки не буде виконана умова  . З цієї умови визначається u2. Потім змінюється координата u3 і т.д. У такій спосіб визначаються частинні екстремуми по всіх координатах. Після цього виконується повторний цикл змінювання координат по черзі, починаючи з u1. Процес пошуку триває, доки всі частинні похідні не дорівнюватимуть нулю (доки всі похідні не будуть меншими за поріг чутливості системи).
. З цієї умови визначається u2. Потім змінюється координата u3 і т.д. У такій спосіб визначаються частинні екстремуми по всіх координатах. Після цього виконується повторний цикл змінювання координат по черзі, починаючи з u1. Процес пошуку триває, доки всі частинні похідні не дорівнюватимуть нулю (доки всі похідні не будуть меншими за поріг чутливості системи).
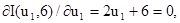

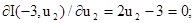 u2 = 1,5.
u2 = 1,5.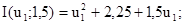
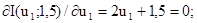 u1 = -0,75.
u1 = -0,75.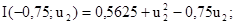
 u2 = 0,375.
u2 = 0,375.


