
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
П.4. Модуль комплексного числаСодержание книги
Поиск на нашем сайте
Пусть a записано в алгебраической форме a = a + bi. Определение. Модулем комплексного числа a называется неотрицательное действительное число Свойства модуля Для "a, bÎ C, где a = a + bi, b = c + di, a, b, c, d Î R. 1/ | a | = 0 «a = 0. Доказательство. | a | = 0 « «a = a + bi = 0. n 2/ 3/ Доказательство. Свойство следует из свойства 6 операции сопряжения. n 4/ | ab | = | a | | b |. Доказательство. Отсюда следует нужное утверждение. n 5/ Если a ¹ 0, то | a -1 | = | a | -1. Доказательство. a a -1 = 1 ® | a a -1 | = | 1 | ® | a | | a| -1 = 1 ® ® | a -1| = | a | -1. n 6 / Неравенство треугольника: | a+b | £ | a | + | b |. Доказательство. Докажем сначала неравенство (1) | a+1| £ | a | + 1. Имеем
£ |a| т.к.
Из (2) следует, что | a+1| Из последнего неравенства следует неравенство (1). Докажем теперь неравенство треугольника. Неравенство треугольника, очевидно, выполнено для b = 0. Докажем неравенство треугольника для b ¹ 0. Имеем | a+b | = | b(ab = | b | (| a | | b = | a | + | b |. n 7/ | a+b | ³ | a | - | b |. Доказательство. | a | = |(a+b)+(-b)| £ | a+b | + | -b| = | a+b | + | b |. Отсюда следует нужное неравенство. n 8/ | a+b | ³ | | a | - | b| |. Доказательство. Справедливы неравенства | a+b | ³ | a | - | b |, | a+b | ³ | b | - | a | = -(| a | - | b|).
Одно из подчёркнутых чисел совпадает с || a | - | b ||. n П.5. Геометрическая интерпретация комплексных чисел Пусть a записано в алгебраической форме a = a + bi. Поставим в соответствие числу a точку плоскости с координатами (a, b). Это соответствие является биекцией множества комплексных чисел на множество точек плоскости. Проиллюстрируем это соответствие Рис.1. В дальнейшем мы будем считать, что точками плоскости являются комплексные числа и будем называть эту плоскость комплексной плоскостью.
Геометрический смысл модуля Из рис.1 видно, что расстояние от начала координат до числа a равно
i
x
-1- i 1- i - i Рис.1.
Пример. Изобразим на комплексной плоскости, на Рис.2, множества заданные, соответственно, следующими условиями: | z | =1; | z | £1; | z | ³1.
- i - i -i Рис.2.
Пусть b записано в алгебраической форме b записано в алгебраической форме b = c + di. Имеем | a-b | = Из рис.3 видно, что геометрический смысл модуля разности комплексных чисел - расстояние между этими числами.
d | b - d |
Рис.3. 0 c a x
Пример. Изобразим на комплексной плоскости, на Рис.4, множества заданные, соответственно, следующими условиями: | z- 1| =2; | z + i | > 1.
x - i -1 0 1 3 x |z+ i | > 1 -2 i Рис.4.
Геометрическая интерпретация комплексных чисел векторами плоскости Поставим в соответствие числу a связаный вектор плоскости с началом в начале координат и с концом в точке a. Установленное соответствие является биекцией между множеством комплексных чисел и множеством связаных векторов плоскости с началом в начале координат. Проиллюстрируем эту связь на Рис.5.
0 Рис.5 x
Геометрический смысл модуля комплексного числа a, при интерпретации чисел векторами, - длина вектора a. Сумма комплексных чисел находится как сумма векторов.
П.6. Тригонометрическая форма записи Комплексного числа
Определение. Аргументом комплексного числа a называется число Arg a, равное величине угла между положительным направлением оси абсцисс и вектором a, Arg a определяется с точность до углов кратных 2p. Главным значением аргумента комплексного числа a называется то значение Arg a, которое принадлежит промежутку (-p,p], оно обозначается arg a и -p< arg a £p. n Пусть a записано в алгебраической форме a = a + bi ¹ 0. Тогда из геометрической интерпретации a следует, что: Arg a = arg a + 2p k, k Î Z; arg a = arctg (b/a), если a > 0; arg a = arctg (b/a) + p, если a < 0, b ³ 0; arg a = arctg (b/a) - p, если a < 0, b < 0. Заметим, что arg a выражается только в радианах, arg 0 не определён. Пример. аrg 1 = 0, Arg 1 = 2p k, k Î Z, аrg (-1) = p, Arg (-1) = p + 2p k, k Î Z, аrg i = p/2, Arg i = p/2 + 2p k, k Î Z, аrg (- i) = -p/2, Arg (- i) = -p/2 + 2p k, k Î Z, аrg (1+ i) = p/4, Arg (1+ i) = p/4 + 2p k, k Î Z. n Теорема 4. Каждое комплексное число a ¹ 0 может быть записано в виде a = | a| (cos (arg a) + i sin (arg a)) = = | a| (cos (Arg a) + i sin (Arg a)). Доказательство. Изобразим a вектором комплексной плоскости, см. Рис.6.
y b a
Рис.6. 0 a x
Угол, образованный вектором a и положительным направлением оси абсцисс, равен arg a, следовательно, a = |a| cos (arg a), b = |a| sin (arg a). Поэтому a = a + bi = | a| cos (arg a) +| a| sin (arg a) = |a| (cos (arg a) + + i sin (arg a). n Определение. Если комплексное число a записано в виде a = | a|(cos j + + i sin j), то говорят, что a записано в тригонометрической форме. n Пример. Запишем числа 1,-1, i, - i в тригонометрической форме:
= cos (-p/2) + i sin (-p/2); 1+ i = Ö2(cos (p/4) + i sin (p/4)). n
Правила действий с комплексными числами, записанными в тригонометрической форме
Пусть комплексные числа a,b записаны в тригонометрической форме a = | a |(cos j + i sin j), b = | b |(cos y + i sin y). 1/ ab = | a || b| (cos (j + y) + i sin (j + y)), т.е. при умножении комплексных чисел, записанных в тригонометрической форме, их модули перемножаются, а аргументы складываются. Доказательство. ab =| a |(cos j + i sin j) | b |(cos y + i sin y) = = | a || b| ((cos j cos y - sin j sin y) + i (cos j sin y + sin j cos y) = = | a || b | (cos (j + y) + i sin (j + y)). n 2/ Если b ¹ 0, то a / b = (| a | / | b |) ((cos (j - y) + i sin (j - y)), т.е. при делении комплексных чисел их модули делятся, а аргументы вычитаются. Доказательство. Обозначим g = (| a | / | b |) ((cos (j - y) + i sin (j - y)). Т.к. g b = (| a | / | b |) ((cos (j - y) + i sin (j - y)) (| b | (cos y + i sin y)) = = a|(cos j + i sin j) = a, то нужное утверждение доказано. n 3/ Если b ¹ 0, то b 4/ Формула Муавра. Для " n Î N, a Доказательство. Формула Муавра является следствием правила 1. n 5/ Обобщённая формула Муавра. Для " n Î Z, a Доказательство. Обобщённая формула Муавра является следствием формулы Муавра и свойства 3/. n
|
||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 407; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.80.121 (0.008 с.) |

 . n
. n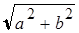 = 0 «a
= 0 «a  + b
+ b  .
.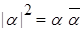 .
. .
.


 (2) | a+1|
(2) | a+1|  a + a = 2 a £ 2
a + a = 2 a £ 2  = 2| a |.
= 2| a |. 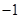 +1)| = | b| | ab
+1)| = | b| | ab 

 Числа a и a расположены симметрично относительно оси абсцисс. Действительные числа расположены на оси абсцисс, поэтому ось абсцисс - ось действительных чисел. На оси ординат расположены числа, у которых действительная часть равна нулю. Иногда ось ординат называют осью мнимых чисел.
Числа a и a расположены симметрично относительно оси абсцисс. Действительные числа расположены на оси абсцисс, поэтому ось абсцисс - ось действительных чисел. На оси ординат расположены числа, у которых действительная часть равна нулю. Иногда ось ординат называют осью мнимых чисел. y
y 
 bi a
bi a -1+ i 1+ i
-1+ i 1+ i  -1 0 1 a
-1 0 1 a  - bi `a
- bi `a




 y | z | =1 y | z | £1 y | z | ³1
y | z | =1 y | z | £1 y | z | ³1














 i i i
i i i 




 -1 1 -1 1 -1 1
-1 1 -1 1 -1 1 







 0 0 0
0 0 0 







 =
=  .
. y
y
 ba
ba



 b | a - c |
b | a - c |
 y y
y y


 | z -1| =2 0
| z -1| =2 0  y
y

 a+b
a+b b
b
 a
a



 1 = cos 0 + i sin 0; -1 = cos p + i sin p; i = cos (p/2) + i sin (p/2); - i =
1 = cos 0 + i sin 0; -1 = cos p + i sin p; i = cos (p/2) + i sin (p/2); - i = = | a |
= | a | 



