
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сформулируйте основную теорему алгебры комплексных чисел. ⇐ ПредыдущаяСтр 2 из 2
Многочлен n-ой степени имеет на комплексной плоскости ровно n нулей (с учетом их кратности). Или: Всякий отличный от константы многочлен с комплексными коэффициентами имеет по крайней мере один корень в поле комплексных чисел.
44. Может ли квадратное уравнение в области комплексных чисел: а) не иметь корней; б) иметь более двух корней? Ответ обоснуйте. а)б) - не верно. Опираясь на основную теорему алгебры комплексных числел, любое квадратное уравнение(уравнение второй степени) в области комплексных чисел имеет ровно 2 комплексныхкорня (в некоторых случаях комплексные корни могут быть действительными, если они лежат на действительной оси).
45. Решите уравнение в области комплексных чисел: а)
46. Многочлен степени 4 с действительными коэффициентами имеет корень
6. Линейные операторы в пространстве 47. Дайте определение линейного оператора. Проверьте линейность оператора, переводящего вектор
48. Дайте определение матрицы линейного оператора в данном базисе. Приведите пример. Пусть Ф(е1)=а11е1+а21е2+…+ан1ен; Ф(ен)=а1ен1+а2ен2+…+аннен. Составим матрицу, она и будет называться матрицой линейного оператора.
49. Как изменяется матрица линейного оператора при переходе от одного базиса к другому? Ответ проиллюстрируйте на примере. Теорема (о переходе к другому базису) Пусть Ae - матрица линейного оператора A в базисе E = (e1,..., en). Пусть Af - матрица линейного оператора A в базисе F = (f1,..., fn).Тогда матрицы связаны соотношением:
50. Найдите матрицу преобразования 51. Дайте определение собственных значений и собственных векторов линейного оператора. Приведите пример. Пусть L — линейное пространство над полем K, — линейное преобразование. Собственным вектором линейного преобразования A называется такой ненулевой вектор, что для некоторого Ax = λx Собственным значением линейного преобразования A называется такое число, для которого существует собственный вектор, то есть уравнение Ax = λx имеет ненулевое решение.
Упрощённо говоря, собственный вектор - любой ненулевой вектор x, который отображается оператором в коллинеарный λx, а соответствующий скаляр λ называется собственным значением оператора.
52. Как связаны между собой собственные значения линейных операторов 53. Как связаны между собой собственные значения линейных операторов 54. Могут ли все собственные значения ненулевой матрицы быть равными 0? Ответ обоснуйте для квадратных матриц порядка Составим характеристическое уравнение:
55. / 56. Как связаны собственные векторы и собственные значения квадратных матриц Пусть v - собственный вектор матрицы A, отвечающий собственному значению лямбда. Тогда
57. / 58. Какому алгебраическому уравнению удовлетворяют собственные значения матрицы? Приведите пример.
Собственные значения матрицы A удовлетворяют характеристическому уравнению этой матрицы, то есть det (A - E) = 0. Пример: матрица Тогда det (A -λE) = det
Получаем, что λ = 1, λ = 3 - собственные значения указанной матрицы.
59. / 60. / 61. Дайте определение числа Фробениуса неотрицательной квадратной матрицы. Найдите число Фробениуса для матрицы
Числом Фробениуса матрицы A ≥ 0 называется максимальное собственное значение этой матрицы. Теорема: Если сумма элементов строки (столбца) матрицы A > 0 одинакова и равна a, то число Фробениуса матрицы A равно a. a) матрица опираясь на теорему, число Фробениуса этой матрицы равно 5. b) Найдем собственные значения матрицы (1-λ)(3-λ) = 0 λ = 1, λ = 3 Числом Фробениуса называется максимальное собственное значение, то есть = 3
62. / 63. / Квадратичные формы 64. Дайте определение матрицы квадратичной формы. Найдите матрицу квадратичной формы: а)
Квадратичной формой Ф от переменных x1,x2,…xn называется однородный многочлен второй степени от этих переменных. Каждая квадратичная орма допускает однозначную запись в следущем симметричном виде:
Где aij=aji (матрица симметрическая) Симметрическая матрица А, элементами которой являются числа aij, называется матрицей квадратичной формы Ф. Если ввести в рассмотрение столбец X=(x1;x2;…;xn)T, то квадратичную форму Ф можно записать в матричном виде Ф=XTAX. А)
(Пишу своими словами). Для построения матрицы из формулы нужно подставить коэффициенты при x на определенные места в матрице. Коэффициенты при xi2 ставим на соответствующие места x11,x22,x33 (по диагонали) без изменений, а коэффициенты при xixj делим на 2 и ставим симметрично на соответствующие места xij,xji (то есть x12,x21; x13,x31 и т.д.) Б)
65. / 66. / 67. / 68. Приведите форму
где
69. / 70. / 71. Сформулируйте и проиллюстрируйте на примере критерий Сильвестра положительной определенности квадратичной формы от трех переменных. Теорема Квадратичная форма Ф тогда и только тогда является положительно определенной, когда все угловые миноры ее матрицы строго положительны. Доказательство Положительность миноров При n=1 единственным угловым минором формы Допустим теперь, что утверждение теоремы справедливо для квадратичных форм от n – 1 переменных, и в этом предположении докажем его для квадратичной формы от n переменных. Так, пусть дана квадратичная форма
Представим ее в виде
где Положительность минора Из данной теоремы, принимая во внимание F = - Ф, нетрудно получить Следствие Для того чтобы квадратичная форма была отрицательно определенной, необходимо и достаточно, чтобы знаки угловых миноров чередовались, причем
Пример
Матрицей квадратичной формы является матрица Для нее Поэтому данная квадратичная форма – положительно определенная.
8. Прямые и плоскости в точечном пространстве 72. Выведите канонические уравнения прямой в 73. Выведите уравнение прямой в Если точка
Уравнения [1] называются каноническими уравнениями прямой l. В действительности уравнения [1] представляют собой систему из двух уравнений
Каждое из которых определяет плоскость (первая из плоскостей параллельна оси z, вторая – оси y).
74. Выведите уравнение плоскости, проходящей через три точки Поскольку речь идет о плоскости, проходящей через точку A и параллельной векторам
75. Выведите уравнение плоскости в Пусть M(x,y,z) – произвольная точка искомой плоскости, тогда необходимо, чтобы вектор AM = (x-a, y-b, z-c) был ортогонален вектору n, то есть их скалярное произведение должно быть равно нулю: p(x - a) + q(y - b) + c(z - c) = 0 получили уравнение искомой плоскости.
Пример уравнения, проходящего параллельно какой-либо координатной оси: x=-1. Такая плоскость будет параллельна осям Oy и Oz
76. Две прямые заданы каноническими уравнениями Угол между плоскостями сводится к углу между нормалями
77. Как найти угол между плоскостями в
78. Как найти угол между прямой Направляющий вектор прямой: Вектор-нормаль плоскости:
79. Как найти расстояние от точки Для нахождения расстояния между прямой и точкой нужно воспользоваться формулой: Пример: l1: y - x = 0, и l2: y - x - 1 = 0.
80. Как найти расстояние от точки Расстояние между двумя параллельными плоскостями можно найти как расстояние между одной из них и точкой, принадлежащей другой плоскости.
81. Запишите общее уравнение плоскости, содержащей прямые Назовем прямые L: (х-а)/1=(у-b)/2=(z-c)/3 и М:(x-a)/3=(y-b)/2=(z-c)/1 Полагаем, что точка А (а;b;c) начальная точка, а направляющий вектор для L вектор p(1;2;3) – один из направляющих векторов плоскости π. Направляющий вектор для М вектор q(3;2;1) – второй направляющий вектор плоскости π. Уравнение плоскости π запишем в виде
Откуда, раскрывая определитель, получаем общее уравнение плоскости
Π: -4х+8у-4z +4(a-2b+c)
82.Что представляет собой пересечение двух ортогональных плоскостей в Предположим что плоскость имеет координаты (А;B;C) z Если А=0, то х любое, следовательно данная плоскость Параллельна плоскости Ох и ортоганально плоскости yOz
Кривые второго порядка 83. Запишите общее уравнение линии второго порядка. Какое геометрическое место точек определяется уравнением
Где коэффициенты
|
||||||||
|
Последнее изменение этой страницы: 2016-08-14; просмотров: 366; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.190.156.80 (0.062 с.) |
 ; б)
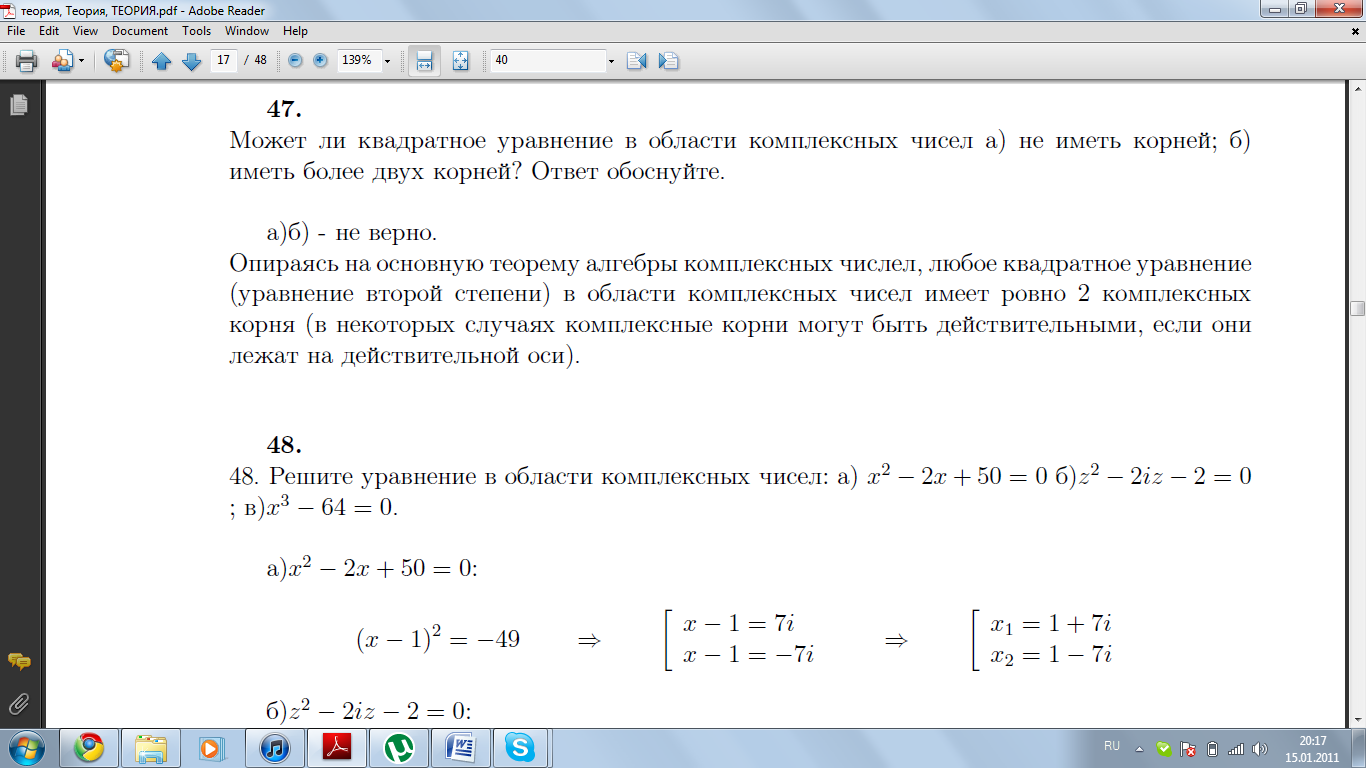
; б)  ; в)
; в)  .
.

 . Докажите, что корнем этого многочлена является число
. Докажите, что корнем этого многочлена является число 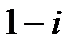 .
.
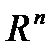
 в вектор
в вектор 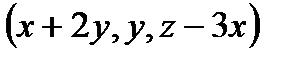 .
.

 пространства
пространства  в стандартном базисе: а)
в стандартном базисе: а)  - поворот на угол
- поворот на угол  ; б)
; б)  .
. ? Ответ обоснуйте.
? Ответ обоснуйте. ? Ответ обоснуйте.
? Ответ обоснуйте. .
. и
и 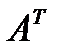 ? Ответ обоснуйте.
? Ответ обоснуйте.


 : (а)
: (а)  ; (б)
; (б)  . Ответы обоснуйте.
. Ответы обоснуйте. Сумма элементов всех строк равна 5. Следовательно,
Сумма элементов всех строк равна 5. Следовательно,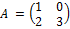
 ; б)
; б) 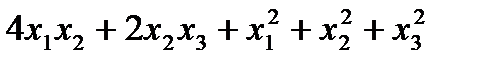 .
.


 к нормальному виду методом Лагранжа.
к нормальному виду методом Лагранжа.
 ;
;  ;
; 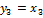
 будем доказывать индукцией по n.
будем доказывать индукцией по n. является
является  ; положительная определенность формы Ф равнозначна положительности
; положительная определенность формы Ф равнозначна положительности  .
.

 есть квадратичная форма от переменных
есть квадратичная форма от переменных  При
При  будем иметь
будем иметь  поэтому из положительной определенности формы Ф следует положительная определенность
поэтому из положительной определенности формы Ф следует положительная определенность  Угловые миноры формы
Угловые миноры формы  совпадают с угловыми минорами
совпадают с угловыми минорами  формы Ф, поэтому из предположения индукции следует
формы Ф, поэтому из предположения индукции следует  [1]
[1]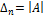 вытекает из простого рассуждения. Мы знаем, что при замене координат матрица А квадратичной формы преобразуется в матрицу
вытекает из простого рассуждения. Мы знаем, что при замене координат матрица А квадратичной формы преобразуется в матрицу  , где P – матрица перехода от новых координат к старым. Применяя теорему об определителе произведения матриц, получим
, где P – матрица перехода от новых координат к старым. Применяя теорему об определителе произведения матриц, получим  , т.е.
, т.е.  и
и  имеют один и тот же знак. Но для формы
имеют один и тот же знак. Но для формы  к которой Ф приводится преобразованием координат, минор
к которой Ф приводится преобразованием координат, минор  , равный произведению
, равный произведению  , больше нуля; значит, он положителен и для исходного вида формы Ф. Добавляя сюда уже доказанные ранее неравенства [1], получаем требуемое. Теорема доказана.
, больше нуля; значит, он положителен и для исходного вида формы Ф. Добавляя сюда уже доказанные ранее неравенства [1], получаем требуемое. Теорема доказана.
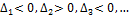


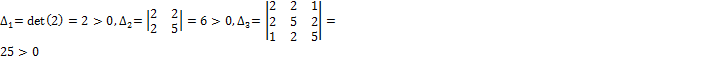 .
.
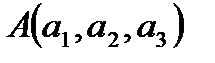 и
и  .
.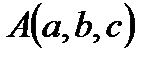 в данном направлении
в данном направлении  .
.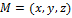 принадлежит l, то вектор
принадлежит l, то вектор  коллинеарен
коллинеарен  . Это записывается с помощью равенств
. Это записывается с помощью равенств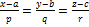 [1]
[1]
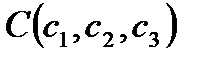 ..
.. , то искомое уравнение будет
, то искомое уравнение будет
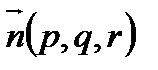 . Приведите пример уравнения плоскости в
. Приведите пример уравнения плоскости в  и
и 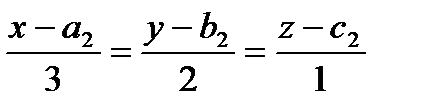 . Найдите угол между ними. Ответ обоснуйте.
. Найдите угол между ними. Ответ обоснуйте.

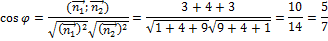

 ,
,  ? Ответ обоснуйте и приведите пример.
? Ответ обоснуйте и приведите пример.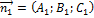


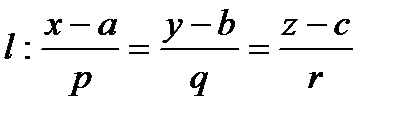 и плоскостью
и плоскостью 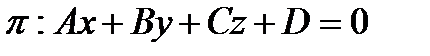 в
в 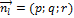


 до прямой
до прямой  ? Как найти расстояние между двумя параллельными прямыми в
? Как найти расстояние между двумя параллельными прямыми в  ?
? ? Как найти расстояние между двумя параллельными плоскостями в
? Как найти расстояние между двумя параллельными плоскостями в  и
и  . Ответ обоснуйте.
. Ответ обоснуйте.
 ?
?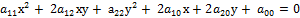
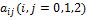 – действительные числа, причем
– действительные числа, причем  не равны нулю одновременно и имеет место симметричность
не равны нулю одновременно и имеет место симметричность 



