Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Матрицы. Функции нескольких переменных. Квадратичные формыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Литература [ 1, ч. 1, гл. 4, § 2; гл. 5, § 4; 6, § 15 - 21; 6, гл. 8, § 1, 2, 3, 4; 2, гл. 8, § 1, 4, 5, 6, 7, 8, 13, 14, 16; 1, ч. 1, гл. 5, § 7; 4, § 22 - 26].
Прямоугольная квадратная таблица, составленная из h n элементов a ij некоторого множества, называется матрицей порядка n и записывается в виде:
Минором элемента aij является определитель М ij, получаемый из матрицы А вычеркиванием строки с номером i и столбца с номером j. Если определитель Δ, составленный из элементов матрицы, отличен от нуля, то матрица А имеет обратную матрицу А -1. При этом справедливы равенства:
где Е – единичная матрица порядка n,
Известно, что матрица А-1 единственная, и она определяется формулой:
где Рассмотрим матрицу-столбец X и столбец B:
и запишем систему линейных алгебраических уравнений в матричной форме:
Решение этой системы имеет вид: Вектор X называется собственным для матрицы A, если выполняется равенство A×X=l×X, где l - её собственное число. Для нахождения собственных чисел матрицы A необходимо найти корни характеристического уравнения:
Собственный вектор Х находится как решение системы уравнений, которая в матричной форме имеет вид
При отыскании собственных векторов следует иметь в виду, что они определяются с точностью до произвольного множителя. Таким образом, фактически определяется собственная прямая, остающаяся неизменной при данном линейном преобразовании с помощью матрицы А.
НЕОБХОДИМОЕ УСЛОВИЕ ЭКСТРЕМУМА ФУНКЦИИ ДВУХ ПРЕМЕННЫХ. Если дифференцируемая функция f(x, y) имеет в точке (x0,y0) экстремум, то:
Далее введём обозначения:
ДОСТАТОЧНЫЕ УСЛОВИЯ ЭКСТРЕМУМА Если функция z = f(x, y) имеет в окрестности точки (x0 ,y0) первые и вторые непрерывные частные производные, то в точке (x0 ,y0), в которой fx’=0, fy’=0 имеет место экстремум, если M2(x0, y0) > 0, причём максимум, если M1(x0, y0) < 0 и минимум, если M1(x0, y0) > 0. Если же M2 < 0, то функция экстремума не имеет. При отыскании наибольшего и наименьшего значений функции двух переменных в замкнутой области следует найти все внутренние точки, где функция может иметь экстремум. Затем нужно исследовать функцию на границе области и найти точки, где функция может принимать наибольшее и наименьшее значения. Для получения ответа сравнить числовые значения функции во всех найденных точках.
ГРАДИЕНТ. ПРОИЗВОДНАЯ ПО НАПРАВЛЕНИЮ
Рассмотрим функцию трёх переменных U=f(x, y, z), которая имеет частные производные первого порядка. Тогда вектор Производная по направлению вектора
Пример 8. Найти производную функции U = z×e-xyв точке M 0(0,1,1) по направлению вектора Решение. Найдем частные производные:
и вычислим Тогда
Однородный многочлен второй степени относительно переменных x, y: Если положить a 12=a21, то квадратичной форме можно подставить в соответствие квадратную матрицу:
Собственные векторы X, Y матрицы A определяют на плоскости два собственных направления
Рассмотрим квадратичную форму трёх переменных:
где a11=a21, a23=a32, a13=a31.В базисе собственных векторов X, Y и Z эта квадратичная форма имеет вид:
Приведение квадратичной формы к каноническому виду используют для приведения к каноническому виду уравнений линий и поверхностей второго порядка.
ЗАДАНИЯ ДЛЯ КОНТРОЛЬНЫХ РАБОТ И ТЕСТИРОВАНИЯ ПО РАЗДЕЛАМ КУРСА ВЫСШЕЙ МАТЕМАТИКИ
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Задание 1. Даны уравнения трех прямых на плоскости l 1, l 2, l 3. Требуется: а) найти точки пересечения прямых: М 1,2, М 1,3, М 2,3; б) доказать, что полученный треугольник прямоугольный; в) найти угол при вершине М 1,3; г) найти уравнение медианы, проведенной из вершины М 1,2 и расстояние от этой прямой до вершины М 2,3; д) найти уравнение высоты, проведенной из вершины М 1,2;
Варианты заданий 1 l 1: 2 x – y = 6; 2 l 1: 3 x + y = 2; l 2: 4 x + 8 y = –8; l 2: 2 x – 6 y = 8; l 3: x + 6 y = –2. l 3: 5 x + y = –8. 3 l 1: 4 x + 3 y = 5; 4 l 1: 5 x – y = 9; l 2: 3 x – 4 y = –15; l 2: x + 5 y = 7; l 3: x + 5 y = –5. l 3: 4 x + 2 y = –8. 5 l 1: 8 x – y = 7; 6 l 1: 6 x + y = 12; l 2: 4 x + 2 y = 6; l 2: – x + 6 y = 35; l 3: x + 3 y = –1. l 3: 8 x + y = –35. 7 l 1: x + 4 y = 14; 8 l 1: 5 x + y = 11; l 2: 4 x – y = 5; l 2: x – 5 y = –3; l 3: 3 x + 2 y = 1. l 3: x + y = 5. 9 l 1: 6 x – y = 10; 10 l 1: 7 x – y = 5; l 2: x + 6 y = 14; l 2: x + 7 y = 15; l 3: x – y = 7. l 3: x + 3 y = 11. 11 l 1: 3 x – y = 7; 12 l 1: 4 x + y = 9; l 2: x + 3 y = 9; l 2: 2 x – 8 y = –4; l 3: x + y = 7. l 3: x + y = 8. 13 l 1: 2 x + 4 y = 6; 14 l 1: 10 x – y = 9; l 2: 6 x – 3 y = 3; l 2: x + 10 y = 11; l 3: x + y = 5. l 3: x + y = –7. 15 l 1: 4 x – 3 y = 5; 16 l 1: 3 x – y = 8; l 2: 3 x + 4 y = 10; l 2: x + 3 y = 6; l 3: x + y = 2. l 3: x + 2 y = 8. 17 l 1: 6 x – y = 11; 18 l 1: 4 x + 4 y = 12; l 2: – x + 6 y = 4; l 2: – x + y = 1; l 3: x + y = 10; l 3: 2 x – y = 5; 19 l 1: x + 8 y = 10. 20 l 1: 5 x + 2 y = 12. l 2: – 8 x + y = –15; l 2: – 2 x + 5 y = 1; l 3: x + y = –6. l 3: x + 2 y = –5. 21 l 1: x + 10 y = 14; 22 l 1: 5 x – 2 y = 12; l 2: – 10 x + y = –39; l 2: 2 x + 6 y = –1; l 3: x + y = –6. l 3: x + 4 y = 1. 23 l 1: 12 x + y = 10; 24 l 1: 8 x + y = 10; l 2: – x + 12 y = –23; l 2: x – 8 y = –15; l 3: x + y = 10. l 3: x + y = –6. 25 l 1: 3 x + 5 y = 11; l 2: – 5 x + 3 y = –7; l 3: x + y = 11.
Задание 2. Даны координаты вершин треугольника: А Требуется: а)найти вектор б) найти длину стороны в) найти координаты середины стороны г) записать уравнение медианы, проведенной из вершины д) вычислить площадь треугольника; е)проверить перпендикулярность сторон Варианты заданий 1 А 2 А 3 А 4 А 5 А 6 А 7 А 8 А 9 А 10 А 11 А 12 А 13 А 14 А 15 А 16 А 17 А 18 А 19 А 20 А 22 А 21 А 23 А 24 А 25 А
Задание 3. Определить тип кривой второго порядка и построить её. Варианты заданий 1 а) 2 а) 3 а) 4 а) 5 а) 6 а) 7 а) 8 а) 9 а) 10 а) 11 а) 12 а) 13 а) 14 а) 15 а) 16 а) 17 а) 18 а) 19 а) 20 а) 21 а) 22 а) 23 а) 24 а) 25 а)
Задание 4. Уравнение кривой второго порядка привести к каноническому виду, определить ее характеристики, сделать чертеж. Варианты заданий 1 5x2 + 9y2 – 30x + 18y + 9 = 0. 2 16x2 + 25y2 + 32x – 100y – 284 = 0. 3 4x2 + 3y2 – 8x + 12y – 32 = 0. 4 9x2 – 18x + 4y2 + 8y – 23 = 0. 5 4x2 – 8x + 16y2 – 32y – 44 = 0. 6 4x2 – 8x + 16y2 – 64y + 4 = 0. 7 9x2 – 18x + 16y2 + 32y – 191 = 0. 8 25x2 – 100x + 9y2 – 18y – 116 = 0. 9 9x2 – 18x + 25y2 – 50y – 119 = 0. 10 9x2 + 36x + 4y2 – 24y + 36 = 0. 11 16x2 + 64x + y2 + 6y + 57 = 0. 12 x2 + 6x + 16y2 + 64y + 57 = 0. 13 9x2 – 18x + 16y2 + 32y – 119 = 0. 14 25x2 + 50x + y2 + 2y + 1 = 0. 15 x2 – 4x + 25y2 – 50y - 71 = 0. 16 4x2 + 8x – 12 = y. 17 3x2 + 6x – 9 = y. 18 4y2 + 8y – 12 = x. 19 3y2 + 6y – 9 = x. 20 5y2 – 10y – 15 = x. 21 5x2 – 10x – 15 = y. 22 y2 + 10y + 25 = x. 23 x2 + 6x + 9 = y. 24 y2 + 2y + 11 = x. 25. x2 + 4x + 5 = y.
Задание 5. Даны координаты вершин пирамиды Необходимо: а) записать уравнение прямой б) записать уравнение плоскости в) вычислить угол между ребром А1А4 и гранью г) записать уравнение высоты, опущенной из вершины д) вычислить объем пирамиды.
Варианты заданий
|
|||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 468; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.214.1 (0.009 с.) |

 .
. ,
,
 ,
, - алгебраическое дополнение элемента a ij.
- алгебраическое дополнение элемента a ij.
 .
. .
. .
. .
.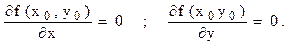


 называют градиентом функции, он задаёт направление возрастания функции U (x, y, z) с наибольшей скоростью.
называют градиентом функции, он задаёт направление возрастания функции U (x, y, z) с наибольшей скоростью. вычисляется по формуле
вычисляется по формуле
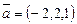 .
. ;
;
 .
. .
. называется квадратичной формой от этих переменных.
называется квадратичной формой от этих переменных.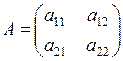 .
. . При этом, если
. При этом, если  собственные числа, то квадратичная форма в базисе собственных векторов X, Y записывается в каноническом виде:
собственные числа, то квадратичная форма в базисе собственных векторов X, Y записывается в каноническом виде: .
.
 .
.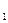 (х
(х 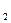 (х
(х  (х
(х  ;
;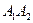 ;
; ;
;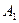 ;
;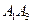 .
.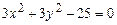 ; б)
; б) 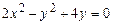 .
. ; б)
; б)  .
.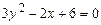 ; б)
; б)  .
.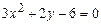 ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
.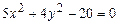 ; б)
; б)  .
. ; б)
; б) 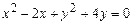 .
.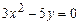 ; б)
; б)  .
. ; б)
; б) 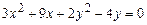 .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
.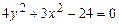 ; б)
; б)  .
. ; б)
; б)  .
.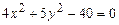 ; б)
; б)  .
. ; б)
; б)  .
.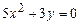 ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
. ; б)
; б)  .
.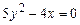 ; б)
; б)  .
.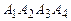 .
. ;
; ;
; на грань
на грань