
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Матрицы. Функции многих переменныхСодержание книги
Поиск на нашем сайте
Задание 13. Дана система линейных уравнений
Необходимо: а) записать матрицу системы, свободных членов и неизвестных; б) записать систему в матричной форме; в) вычислить определитель системы; г) найти обратную матрицу системы; д) записать решение системы в матричной форме; е) найти собственные числа и собственные векторы матрицы системы.
Варианты заданий 1 2 3 4 5 6 7 8 9 10 11 12. 13 14 15 16 17 18 19 20 21 22 23 24 25
Задание 14. Найти производную функции 1
3
5
7
9
11 13
Задание 15. Найти угол между градиентами функций Варианты заданий 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Задание 16. Найти наибольшее и наименьшее значение функции Варианты заданий 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
Задание 17. Для функции двух переменных необходимо: а) найти критические точки; б) найти в) вычислить г) найти экстремальные значения функции. Варианты заданий 1 3 5 7 9 11 13 15 16 17 18 19 20 21 22 23 24 25 26
Задание 18. Для функции двух переменных а) найти область определения функции; б) найти в) записать уравнение касательной плоскости и нормали к поверхности Варианты заданий 1 2 3 5 6
7 8 9 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
РЕКОМЕНДАЦИИ СОСТАВЛЕНИЯ ТЕСТОВ
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Тест 1 1 Даны уравнения прямых: l 1: 2 x – y = 6; l 2: 4 x + 8 y = –8. Построить их и найти точку пересечения. 2 Даны координаты вершин треугольника А 3 Определить тип кривой и построить её: 4 Даны координаты вершин треугольника:
5 Даны координаты вершин пирамиды:
Тест 2 1 Даны уравнения прямых: l 1: 2 x – y = 6; l 2: x + 2 y = –2. Построить их и доказать аналитически перпендикулярность. 2 Даны координаты вершин треугольника А 3 Определить тип кривой и построить её: 4 Даны координаты вершин треугольника: 5 Найти расстояние от точки
Тест 3 1 Даны уравнения прямых: l 1: 2 x – y = 6; l 2: 3 x + 2 y = 9. Построить прямую l 1 и найти точки пересечения прямых l 1 и l 2 с координатными осями. 2 Даны координаты вершин треугольника: А 3 Определить тип кривой и построить её: 4 Даны координаты вершин треугольника: 5 Написать уравнение прямой через точку
Тест 4 1 Даны уравнения прямых: l 1: 2 x – y = 6; l 2: -4 x +2 y = 9. Найти точку пересечения прямых и доказать их перпендикулярность. 2 Даны координаты вершин треугольника: А 3 Определить тип кривой и построить её: 4 Даны координаты вершин треугольника:
5 Написать уравнение прямой через точку
Тест 5 1 Даны точки: А 2 Даны координаты вершин треугольника: А 3 Определить тип кривой и построить её: 4. Даны координаты вершин треугольника:
5 Написать уравнение прямой через точку
ПРЕДЕЛЫ. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ И ЕГО ПРИЛОЖЕНИЯ
Тест 6 1 Найти предел 2 Вычислить производную функции 3. Написать уравнение касательной к графику функции 4 Найти интервалы монотонности функции 5 Сумма двух положительных чисел
Тест 7 1 Найти предел
2Вычислить производную функции
3 Написать уравнение нормали к графику функции
4 Найти точки экстремума
5 Точка движется по закону
Тест 8 1 Найти предел 2Вычислить
3 Найти под каким углом кривая
4 Найти критические точки
5 Точка движется по закону
Тест 9 1 Найти предел 2Вычислить
3 Найти тангенс угла наклона касательной графика функции
4. Найти точки перегиба
5 Точка движется по закону
Тест 10 1 Найти предел 2Вычислить производную:
3 Составить уравнение касательной к графику функции в точке
4 Найти интервалы выпуклости и вогнутости 5 Задана скорость движения точки
|
||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 165; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.204.44 (0.011 с.) |

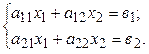

 1;
1; 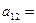 2;
2;  4;
4;  3;
3; 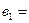 5;
5; 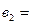 10.
10.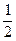 ;
; 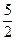 ;
; 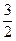 ;
;  ;
;  ;
;  ;
; 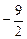 ;
; 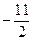 ;
; 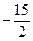 ;
;  ;
;  в точке М по направлению вектора
в точке М по направлению вектора 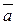 .
.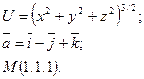 2
2 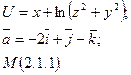
 4
4 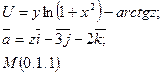
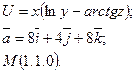 6
6 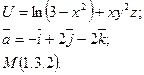
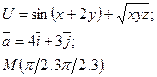 8
8 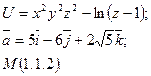
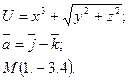 10
10 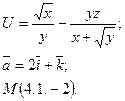
 12
12 
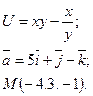
 14
14 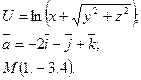
 и
и  в точке М.
в точке М.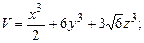
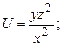
 .
.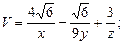
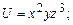


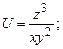
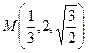 .
.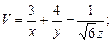
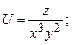
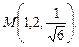


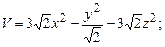
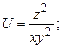



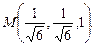
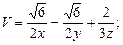
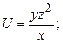
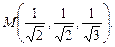
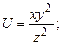
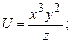
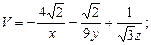
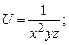

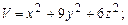

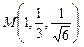

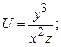
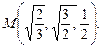
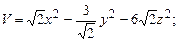
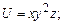

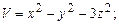
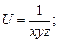
 в области D. ограниченной заданными линиями.
в области D. ограниченной заданными линиями.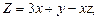
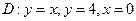


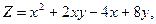
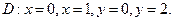
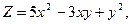
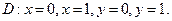

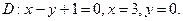
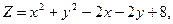
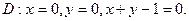
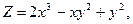


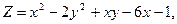


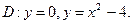
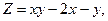
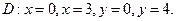

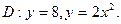




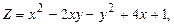

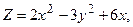
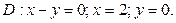


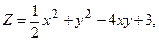
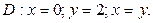

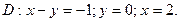
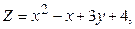
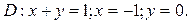
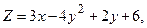

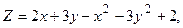
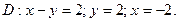

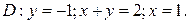
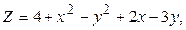
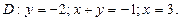


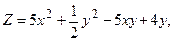
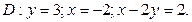
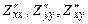 ;
;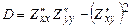 ;
;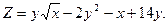 2
2 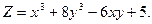
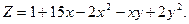 4
4 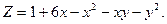
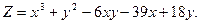 6
6 
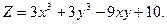 8
8 
 10
10 
 12
12 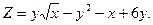
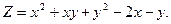 14
14 
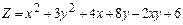 .
.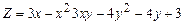 .
.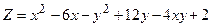 .
. .
.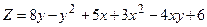 .
.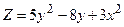
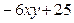 .
.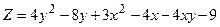 .
.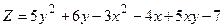 .
.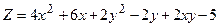 .
.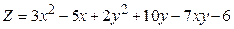 .
.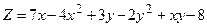 .
.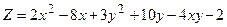 .
.
 и
и 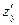 ;
;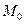 .
.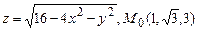 .
. .
. . 4
. 4 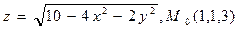 .
. .
. .
.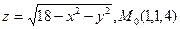 .
. .
. . 10
. 10 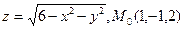 .
.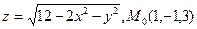 .
.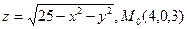 .
.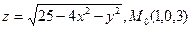 .
.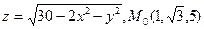 .
.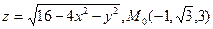 .
.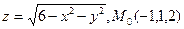 .
.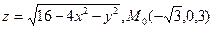 .
. .
. .
.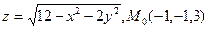 .
. .
. .
.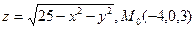 .
. .
. .
.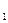 (3,1), А
(3,1), А 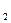 (5,-2), А
(5,-2), А  (9,7). Найти длину стороны
(9,7). Найти длину стороны 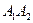 .
.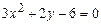 .
.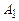 (6, 4, 2),
(6, 4, 2),  (10, -1, -3),
(10, -1, -3), 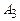 (12, -2, -3). Найти вектор
(12, -2, -3). Найти вектор  и уравнение прямой
и уравнение прямой 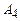 (-8, 8, -2). Найти ее объем.
(-8, 8, -2). Найти ее объем. .
. .
. до плоскости
до плоскости 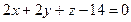 .
.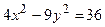 .
.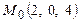 перпендикулярно плоскости
перпендикулярно плоскости 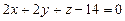 .
. .
.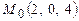 перпендикулярно плоскости
перпендикулярно плоскости 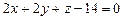 .
. и
и 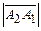 .
.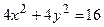 .
. .
.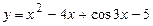 .
. в точке
в точке  .
.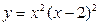 .
.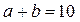 . Найти наибольшую величину их произведения.
. Найти наибольшую величину их произведения. .
.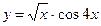 .
.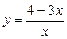 в точке
в точке 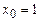 .
. .
.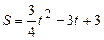 . Найти момент времени t, когда скорость равна нулю и S - путь, пройденный точкой к этому времени.
. Найти момент времени t, когда скорость равна нулю и S - путь, пройденный точкой к этому времени. .
.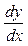 в точке
в точке 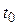 .
.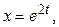

 .
.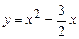 пересекает ось ОХ в точке
пересекает ось ОХ в точке  .
.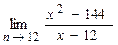 .
. в точке
в точке 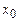 .
.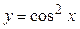 ,
, 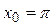 .
.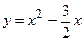 в точке
в точке  .
.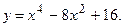
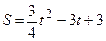 . Найти её ускорение.
. Найти её ускорение.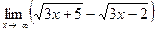 .
. .
. .
. .
.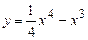 .
.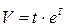 . Найти её ускорение.
. Найти её ускорение.


