
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Квадратичная функция. Посторенние графика квадратичной функцииСодержание книги
Поиск на нашем сайте Функция, заданная формулой Существует несколько способов построения графика квадратичной функции. Опишем два из них. 1 способ. Квадратичную функцию Преобразуем квадратный трехчлен Эта формула имеет вид График функции 2 способ. График функции § абсциссу вершины параболы по формуле § нули функции; § точку пересечения параболы с осью Оу – точку (0; с); § дополнительные точки, если необходимо.
Степенная функция Функция вида
Графики степенной функции при различных значениях n представлены в таблице.
Арифметическая прогрессия Бесконечной числовой последовательностью называется функция, определенная на множестве натуральных чисел. Ее принято обозначать Числовая последовательность, каждый член которой, начиная со второго, равен предшествующему члену, сложенному с одним и тем же числом, называется арифметической прогрессией. Это число d называется разностью арифметической прогрессии. d = a2 – a1 = a3 – a2 = … = ak – ak-1 = … Арифметическая прогрессия задается своим первым членом a1 и разностью d. Любой член арифметической прогрессии можно вычислить по формуле (формула n-го члена) Если d > 0, то арифметическая прогрессия является возрастающей. Если d < 0, то арифметическая прогрессия является убывающей. Если d = 0, то все члены арифметической прогрессии равны между собой и она является постоянной последовательностью. Характеристическое свойство арифметической прогрессии. Числовая последовательность является арифметической прогрессией тогда и только тогда, когда каждый ее член, начиная со второго, является средним арифметическим предшествующего и последующего членов.
Сумма членов равноудаленных от концов прогрессии есть величина постоянная, т.е. Если на плоскости отмечать точки с координатами Это означает, что арифметическая прогрессия является линейной функцией, заданной на множестве натуральных чисел N и её можно задать формулой вида Сумма n – первых членов арифметической прогрессии вычисляется по формуле Доказательство: Запишем сумму n –первых членов арифметической прогрессии двумя способами.
Сложим почленно эти равенства.
В каждой скобке стоит сумма вида
Tаких скобок ровно n, тогда Геометрическая прогрессия Геометрической прогрессией называется числовая последовательность, в которой первый член отличен от нуля, а каждый последующий равен предыдущему, умноженному на некоторое постоянное для данной последовательности число не равное нулю. Это число называется знаменателем геометрической прогрессии Геометрическая прогрессия задается своим первым членом b1 и знаменателем q. Любой член геометрической прогрессии можно записать по формуле (формула n-го члена) Геометрическая прогрессия возрастает, если Геометрическая прогрессия убывает, если Если q < 0, то последовательность является ни возрастающей, ни убывающей, т.к. знаки ее членов чередуются. Характеристическое свойство геометрической прогрессии. Последовательность чисел является геометрической прогрессией тогда и только тогда, когда каждый ее член, начинается со второго, является средним геометрическим предыдущего и последующего членов Произведение членов, равноотстоящих от концов прогрессии, есть величина постоянная, т.е. Формула суммы n-первых членов геометрической прогрессии
Доказательство: Сумма n –первых членов геометрической прогрессии равна Если q = 1, то все члены равны b1, тогда Если q ≠ 1, то умножим равенство По определению геометрической прогрессии
Вычтем равенство (1) из равенства (2), получим
или Геометрическая прогрессия называется бесконечно убывающей, если |q| < 1. Суммой бесконечно убывающей геометрической прогрессии называется число, к которому стремится сумма ее n –первых членов при n→∞. Сумма S бесконечно убывающей геометрической прогрессии равна
|
|||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 426; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.156 (0.008 с.) |

 , где х,у – переменные, а,в,с – заданные числа,
, где х,у – переменные, а,в,с – заданные числа,  , называется квадратичной.
, называется квадратичной. путем выделения полного квадрата.
путем выделения полного квадрата. . Имеем:
. Имеем:  Получили формулу
Получили формулу 
 и
и 
 с помощью параллельного переноса, при котором точка
с помощью параллельного переноса, при котором точка  переходит в точку
переходит в точку  . Значит, график любой квадратичной функции
. Значит, график любой квадратичной функции  , а ординату –
, а ординату –  ;
;






 называется степенной функциейс показателем степени n.
называется степенной функциейс показателем степени n.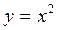 .
1. D(y) = R.
2. E(y) =
.
1. D(y) = R.
2. E(y) =  .
3. Функция четная.
4. y=0 при x=0.
5. y > 0 при
.
3. Функция четная.
4. y=0 при x=0.
5. y > 0 при  .
6. Функция возрастает на
.
6. Функция возрастает на  .
7. Функция непрерывна, ограничена снизу нулем.
.
7. Функция непрерывна, ограничена снизу нулем.

 .
1. D(y) = R.
2. E(y) =R.
3. Функция нечетная.
4. y=0 при x=0.
5. y > 0 при
.
1. D(y) = R.
2. E(y) =R.
3. Функция нечетная.
4. y=0 при x=0.
5. y > 0 при  ;
y < 0 при
;
y < 0 при  .
6. Функция возрастает на R.
7. Функция непрерывна, неограниченна.
.
6. Функция возрастает на R.
7. Функция непрерывна, неограниченна.

 , то
, то  .
1. D (у) =
.
1. D (у) = 
 N
N








 .
.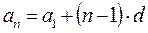 .
.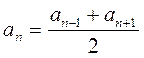 или
или  , где n, k
, где n, k 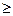 2.
2.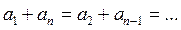 .
.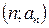 , то, все эти точки будут лежать на графике функции, задаваемой формулой
, то, все эти точки будут лежать на графике функции, задаваемой формулой 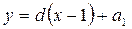 .
.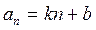 , где k, b – числа.
, где k, b – числа.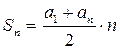 или
или 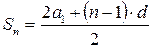 .
.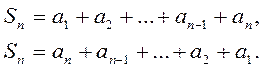
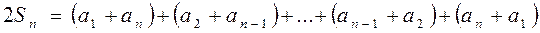
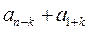 , где k = 0, 1, …, n-1.
, где k = 0, 1, …, n-1.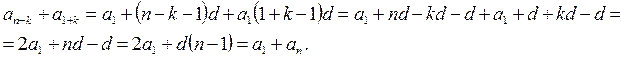
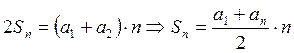 или
или 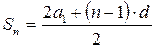 , что и требовалось доказать.
, что и требовалось доказать.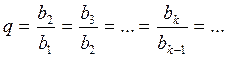 .
.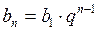 .
.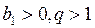 или
или 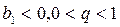 .
.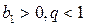 или
или  .
.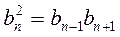 или
или 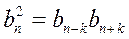 , где n, k
, где n, k 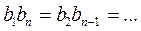 .
. , при q ≠ 1 и
, при q ≠ 1 и 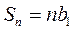 при q = 1.
при q = 1.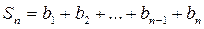 (1).
(1). – что и требовалось доказать.
– что и требовалось доказать.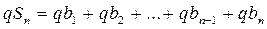 .
.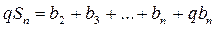 (2).
(2).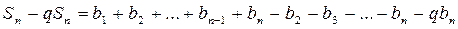 ;
; ;
; 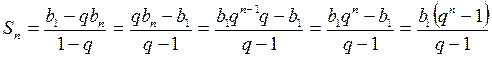
 , что и требовалось доказать.
, что и требовалось доказать. .
.


