Линейная функция, ее свойства и график
Функция, заданная формулой  , где к и b - некоторые числа, называется линейной. , где к и b - некоторые числа, называется линейной.
Коэффициент к=tgα характеризует угол α, который образует прямая  с положительным направлением оси ОХ, и называется угловым коэффициентом. Если к>0, то угол острый; если к<0, то угол тупой; если к=0, то прямая совпадает с осью Оx или ей параллельна. с положительным направлением оси ОХ, и называется угловым коэффициентом. Если к>0, то угол острый; если к<0, то угол тупой; если к=0, то прямая совпадает с осью Оx или ей параллельна.
Свойства:
1. D(y)=R.
2. Е(y)=R.
3. Функция ни четная, ни нечетная, т.к. 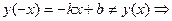 не является четной; не является четной; 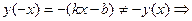 не является нечетной. не является нечетной.
4. у = 0 при  (нули функции). (нули функции).
5. Промежутки знакопостоянства:
§ если к > 0, у < 0 при  ; у > 0 при ; у > 0 при  ; ;
§ если к < 0, у < 0 при  ; у > 0 при ; у > 0 при  . .
6. Функция возрастает при к>0 и убывает при к<0 на R.
7. Функция неограниченна, непрерывна.
Графиком функции является прямая. Для ее построения можно найти точки пересечения с осями координат:
§ с осью ОХ: у = 0,  А( А( ; 0); ; 0);
§ с осью ОУ: х = 0, у = b  В(0; b). В(0; b).

График функции  может быть построен с помощью параллельного переноса на |b| единиц вверх (b>0), или вниз (b<0) графика функции может быть построен с помощью параллельного переноса на |b| единиц вверх (b>0), или вниз (b<0) графика функции 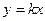 . Зависимость . Зависимость 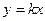 называется прямой пропорциональностью. называется прямой пропорциональностью.
Рассмотрим частные случаи линейной функции.
Если b = 0, то 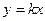 . .
| Если k=0, то y=b.
| Свойства:
1. D(y)=R.
2. Е(y)=R.
3. Функция нечетная, т.к.  .
4. у = 0 при .
4. у = 0 при 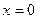 .
5. Промежутки знакопостоянства:
§ если к > 0, у < 0 при .
5. Промежутки знакопостоянства:
§ если к > 0, у < 0 при  ;
у > 0 при ;
у > 0 при  ;
§ если к < 0, у < 0 при ;
§ если к < 0, у < 0 при  ;
у > 0 при ;
у > 0 при  .
6. Функция возрастает при к>0 и
убывает при к<0 на R.
7. Функция неограниченна, непрерывна.
Графиком функции является прямая, проходящая через начало координат. .
6. Функция возрастает при к>0 и
убывает при к<0 на R.
7. Функция неограниченна, непрерывна.
Графиком функции является прямая, проходящая через начало координат.
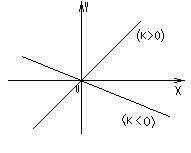
| Свойства:
1. D(y)=R.
2. Е(y)=b.
3. Функция четная, т.к.  .
4. у .
4. у  0.
5. Промежутки знакопостоянства:
§ если b > 0, у > 0;
§ если b < 0, у < 0.
6. Функция постояннана R.
7. Функция непрерывна.
Графиком функции является прямая, параллельная оси Ox. 0.
5. Промежутки знакопостоянства:
§ если b > 0, у > 0;
§ если b < 0, у < 0.
6. Функция постояннана R.
7. Функция непрерывна.
Графиком функции является прямая, параллельная оси Ox.

|
Функция  , ее свойства и график , ее свойства и график
Если переменная у обратно пропорциональна переменной х, то эта зависимость выражается формулой  , где , где  - коэффициент обратной пропорциональности. - коэффициент обратной пропорциональности.
Свойства:
1. D(у) =  . .
2. Е(у) =  . .
3. Нечетная, т.к.  . .
4. Промежутки знакопостоянства:
§ если k > 0, то y > 0 при  ; ;
y < 0 при  ; ;
§ если k < 0, то y > 0 при  ; ;
y < 0 при  . .
5. Монотонность:
§ при  функция возрастает на функция возрастает на 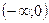 и и  ; ;
§ при  функция убывает на функция убывает на 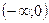 и и  . .
Графиком обратной пропорциональности  является кривая, состоящая из 2-х ветвей, симметричных относительно начала координат. Такая кривая называется гиперболой. является кривая, состоящая из 2-х ветвей, симметричных относительно начала координат. Такая кривая называется гиперболой.

Функция  ее свойства и график ее свойства и график
Функция вида  , где а – некоторое число, а , где а – некоторое число, а  0, называется квадратичной. 0, называется квадратичной.
График функции  может быть получен с помощью графика функции может быть получен с помощью графика функции  : :
§ если а>1, то растяжение вдоль оси Оу в а раз;
§ если 0<a<1, то сжатие вдоль оси Оу в  раз; раз;
§ если а<0, то симметрично относительно оси Ох.
Рассмотрим свойства и график функции  в зависимости от знака а. в зависимости от знака а.
| а > 0
| а < 0
| 1. Д (у) = R.
2. E (y) =  .
3.Функция четная, т.к. .
3.Функция четная, т.к.  .
4. у = 0 при х = 0.
5. у>0 при .
4. у = 0 при х = 0.
5. у>0 при  .
6. Монотонность:
§ функция возрастает на .
6. Монотонность:
§ функция возрастает на  ;
§ функция убывает на ;
§ функция убывает на  .
7. унаим = 0 при х=0.
8. Функция ограничена снизу нулем, непрерывна. .
7. унаим = 0 при х=0.
8. Функция ограничена снизу нулем, непрерывна.

| 1. Д (у) = R.
2. E (y) =  .
3.Функция четная, т.к. .
3.Функция четная, т.к.  .
4. у = 0 при х = 0.
5. у<0 при .
4. у = 0 при х = 0.
5. у<0 при  .
6. Монотонность:
§ функция возрастает на .
6. Монотонность:
§ функция возрастает на  ;
§ функция убывает на ;
§ функция убывает на  .
7. унаиб = 0 при х=0.
8. Функция ограничена сверху нулем, непрерывна. .
7. унаиб = 0 при х=0.
8. Функция ограничена сверху нулем, непрерывна.

|
Графики функций  и и  . Преобразование графика . Преобразование графика
Графиком функции  является парабола, которая может быть получена из графика функции является парабола, которая может быть получена из графика функции  с помощью параллельного переноса вдоль оси Оy на | n |единиц вверх, если n>0; или на с помощью параллельного переноса вдоль оси Оy на | n |единиц вверх, если n>0; или на  единиц вниз, если n<0. единиц вниз, если n<0.
Рассмотрим графики функции  при a > 0. при a > 0.
| n > 0
| n < 0
|  1. D(y)=R.
2. E(y)=
1. D(y)=R.
2. E(y)= 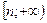 .
3. Четная.
4. Нулей нет.
5. y > 0 при .
3. Четная.
4. Нулей нет.
5. y > 0 при  .
6. Возрастает на .
6. Возрастает на  ;
убывает на ;
убывает на  .
7. унаим = n при х = 0.
8. Ограничена снизу n, непрерывна. .
7. унаим = n при х = 0.
8. Ограничена снизу n, непрерывна.
|  1. D(y)=R.
2. E(y)=
1. D(y)=R.
2. E(y)= 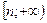 .
3. Четная.
4. у = 0 при .
3. Четная.
4. у = 0 при  .
5. y > 0 при .
5. y > 0 при  ;
y < 0 при ;
y < 0 при  .
6. Возрастает на .
6. Возрастает на  ;
убывает на ;
убывает на  .
7. унаим = n при х = 0.
8. Ограничена снизу n, непрерывна. .
7. унаим = n при х = 0.
8. Ограничена снизу n, непрерывна.
|
Рассмотрим графики функции  при a < 0. при a < 0.
| n > 0
| n < 0
|  1. D(y)=R.
2. E(y)=
1. D(y)=R.
2. E(y)=  .
3. Четная.
4. у = 0 при .
3. Четная.
4. у = 0 при  .
5. y > 0 при .
5. y > 0 при  ;
y < 0 при ;
y < 0 при  .
6. Возрастает на .
6. Возрастает на  ;
убывает на ;
убывает на  .
7. унаиб = n при х = 0.
8. Ограничена сверху n, непрерывна. .
7. унаиб = n при х = 0.
8. Ограничена сверху n, непрерывна.
| 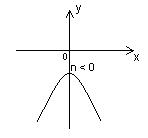 1. D(y)=R.
2. E(y)=
1. D(y)=R.
2. E(y)=  .
3. Четная.
4. Нулей нет.
5. y < 0 при .
3. Четная.
4. Нулей нет.
5. y < 0 при  .
6. Возрастает на .
6. Возрастает на  ;
убывает на ;
убывает на  .
7. унаиб = n при х = 0.
8. Ограничена сверху n, непрерывна. .
7. унаиб = n при х = 0.
8. Ограничена сверху n, непрерывна.
|
Графиком функции  является парабола, которая может быть получена в результате параллельного переноса графика функции является парабола, которая может быть получена в результате параллельного переноса графика функции  вдоль оси Оx на | m | единиц вправо, если m>0; или на | m | единиц влево, если m<0. вдоль оси Оx на | m | единиц вправо, если m>0; или на | m | единиц влево, если m<0.
| a > 0
| a < 0
|  1. D(y)=R.
2. E(y)=
1. D(y)=R.
2. E(y)=  .
3. Ни четная, ни нечетная.
4. у = 0 при х=т.
5. y > 0 при .
3. Ни четная, ни нечетная.
4. у = 0 при х=т.
5. y > 0 при  .
6. Возрастает на .
6. Возрастает на  ;
убывает на ;
убывает на  .
7. унаим = 0 при х = т.
8. Ограничена снизу нулем, непрерывна. .
7. унаим = 0 при х = т.
8. Ограничена снизу нулем, непрерывна.
|  1. D(y)=R.
2. E(y)=
1. D(y)=R.
2. E(y)=  .
3. Ни четная, ни нечетная.
4. у = 0 при х=т.
5. y < 0 при .
3. Ни четная, ни нечетная.
4. у = 0 при х=т.
5. y < 0 при  .
6. Возрастает на .
6. Возрастает на  ;
убывает на ;
убывает на  .
7. унаиб = 0 при х = т.
8. Ограничена сверху нулем, непрерывна. .
7. унаиб = 0 при х = т.
8. Ограничена сверху нулем, непрерывна.
| График функции  может быть получен с помощью 2-х параллельных переносов описанных выше. может быть получен с помощью 2-х параллельных переносов описанных выше.
Преобразование графиков
1. График функции  можно получить из графика функции можно получить из графика функции 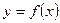 с помощью параллельного переноса вдоль оси Оу на | n |единиц вверх, если n>0; или на с помощью параллельного переноса вдоль оси Оу на | n |единиц вверх, если n>0; или на  единиц вниз, если n<0. единиц вниз, если n<0.
2. График функции  можно получить из графика функции можно получить из графика функции 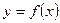 с помощью параллельного переноса вдоль оси Ох на | m | единиц вправо, если m>0; или на с помощью параллельного переноса вдоль оси Ох на | m | единиц вправо, если m>0; или на  единиц влево, если m<0. единиц влево, если m<0.
3. График функции  можно получить из графика функции можно получить из графика функции 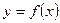 с помощи 2-х параллельных переносов: вдоль оси Оу на | n |единиц вверх, если n>0; или на с помощи 2-х параллельных переносов: вдоль оси Оу на | n |единиц вверх, если n>0; или на  единиц вниз, если n<0., вдоль оси Ох на | m | единиц вправо, если m>0; или на единиц вниз, если n<0., вдоль оси Ох на | m | единиц вправо, если m>0; или на  единиц влево, если m<0. единиц влево, если m<0.
4. График функции  можно получить из графика функции можно получить из графика функции 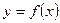 с помощью симметричного отображения относительно оси Ох. с помощью симметричного отображения относительно оси Ох.
5. График функции  можно получить из графика функции можно получить из графика функции 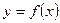 с помощью симметричного отображения относительно оси Оу. с помощью симметричного отображения относительно оси Оу.
6. График функции  можно получить из графика функции можно получить из графика функции 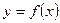 с помощью сжатия вдоль оси Ох к оси Оу в а раз, если a>1; или растяжения вдоль оси Ох от оси Оу в с помощью сжатия вдоль оси Ох к оси Оу в а раз, если a>1; или растяжения вдоль оси Ох от оси Оу в  раз, если 0<a<1. раз, если 0<a<1.
7. График функции  можно получить из графика функции можно получить из графика функции 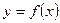 с помощью растяжения вдоль оси Оу от оси Ох в а раз, если а>1; или сжатия вдоль оси Оу к оси Ох в с помощью растяжения вдоль оси Оу от оси Ох в а раз, если а>1; или сжатия вдоль оси Оу к оси Ох в  раз, если 0<a<1. раз, если 0<a<1.
8. График функции  можно получить из графика функции можно получить из графика функции 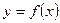 следующим образом: часть графика следующим образом: часть графика 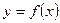 , лежащая над осью Ох сохраняется, часть его, лежащая под осью Ох, отображается симметрично относительно оси Ох. , лежащая над осью Ох сохраняется, часть его, лежащая под осью Ох, отображается симметрично относительно оси Ох.
9. График функции  можно получить из графика функции можно получить из графика функции 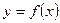 следующим образом: при следующим образом: при  график график 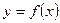 сохраняется, а при х<0 полученная часть графика отображается симметрично относительно оси Оу. сохраняется, а при х<0 полученная часть графика отображается симметрично относительно оси Оу.
|



 , где к и b - некоторые числа, называется линейной.
, где к и b - некоторые числа, называется линейной.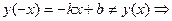 не является четной;
не является четной; 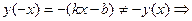 не является нечетной.
не является нечетной. (нули функции).
(нули функции). ; у > 0 при
; у > 0 при  ;
; А(
А( ; 0);
; 0); В(0; b).
В(0; b).
 может быть построен с помощью параллельного переноса на |b| единиц вверх (b>0), или вниз (b<0) графика функции
может быть построен с помощью параллельного переноса на |b| единиц вверх (b>0), или вниз (b<0) графика функции 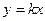 . Зависимость
. Зависимость  .
4. у = 0 при
.
4. у = 0 при 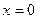 .
5. Промежутки знакопостоянства:
§ если к > 0, у < 0 при
.
5. Промежутки знакопостоянства:
§ если к > 0, у < 0 при  ;
у > 0 при
;
у > 0 при  ;
§ если к < 0, у < 0 при
;
§ если к < 0, у < 0 при 
 .
4. у
.
4. у  0.
5. Промежутки знакопостоянства:
§ если b > 0, у > 0;
§ если b < 0, у < 0.
6. Функция постояннана R.
7. Функция непрерывна.
Графиком функции является прямая, параллельная оси Ox.
0.
5. Промежутки знакопостоянства:
§ если b > 0, у > 0;
§ если b < 0, у < 0.
6. Функция постояннана R.
7. Функция непрерывна.
Графиком функции является прямая, параллельная оси Ox.

 , ее свойства и график
, ее свойства и график - коэффициент обратной пропорциональности.
- коэффициент обратной пропорциональности. .
. .
. ;
; ;
; функция возрастает на
функция возрастает на 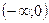 и
и  ;
; функция убывает на
функция убывает на 
 ее свойства и график
ее свойства и график :
: раз;
раз; .
3.Функция четная, т.к.
.
3.Функция четная, т.к.  .
4. у = 0 при х = 0.
5. у>0 при
.
4. у = 0 при х = 0.
5. у>0 при  .
6. Монотонность:
§ функция возрастает на
.
6. Монотонность:
§ функция возрастает на  .
7. унаим = 0 при х=0.
8. Функция ограничена снизу нулем, непрерывна.
.
7. унаим = 0 при х=0.
8. Функция ограничена снизу нулем, непрерывна.


 и
и  . Преобразование графика
. Преобразование графика единиц вниз, если n<0.
единиц вниз, если n<0. 1. D(y)=R.
2. E(y)=
1. D(y)=R.
2. E(y)= 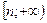 .
3. Четная.
4. Нулей нет.
5. y > 0 при
.
3. Четная.
4. Нулей нет.
5. y > 0 при  .
6. Возрастает на
.
6. Возрастает на  1. D(y)=R.
2. E(y)=
1. D(y)=R.
2. E(y)=  .
5. y > 0 при
.
5. y > 0 при  ;
y < 0 при
;
y < 0 при  .
6. Возрастает на
.
6. Возрастает на  1. D(y)=R.
2. E(y)=
1. D(y)=R.
2. E(y)=  .
3. Четная.
4. у = 0 при
.
3. Четная.
4. у = 0 при  1. D(y)=R.
2. E(y)=
1. D(y)=R.
2. E(y)=  1. D(y)=R.
2. E(y)=
1. D(y)=R.
2. E(y)=  .
6. Возрастает на
.
6. Возрастает на  ;
убывает на
;
убывает на  .
7. унаим = 0 при х = т.
8. Ограничена снизу нулем, непрерывна.
.
7. унаим = 0 при х = т.
8. Ограничена снизу нулем, непрерывна.
 1. D(y)=R.
2. E(y)=
1. D(y)=R.
2. E(y)=  может быть получен с помощью 2-х параллельных переносов описанных выше.
может быть получен с помощью 2-х параллельных переносов описанных выше. можно получить из графика функции
можно получить из графика функции 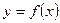 с помощью параллельного переноса вдоль оси Оу на | n |единиц вверх, если n>0; или на
с помощью параллельного переноса вдоль оси Оу на | n |единиц вверх, если n>0; или на  можно получить из графика функции
можно получить из графика функции  единиц влево, если m<0.
единиц влево, если m<0. можно получить из графика функции
можно получить из графика функции  можно получить из графика функции
можно получить из графика функции  можно получить из графика функции
можно получить из графика функции  можно получить из графика функции
можно получить из графика функции  можно получить из графика функции
можно получить из графика функции  можно получить из графика функции
можно получить из графика функции  можно получить из графика функции
можно получить из графика функции  график
график 


